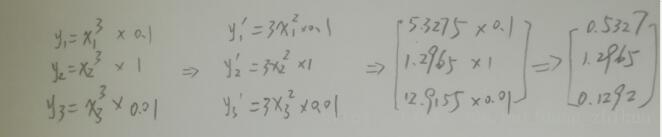Pytorch 学习(1)自动求导: 自动微分 初体验
Pytorch 学习(1)自动求导: 自动微分 初体验
PyTorch 中所有神经网络的核心是 autograd 自动求导包。
官网上的例子:如果 Variable 是标量的形式(例如, 它包含一个元素数据), 不必指定任何参数给 backward()。
import torch
from torch.autograd import Variable
x= Variable(torch.ones(2,2),requires_grad =True)
print(x)
y =x +2
print(y)
print(y.grad_fn)
z= y*y*3
out =z.mean()
print(z,out)
out.backward()
print(x.grad)
运行结果为:
tensor([[ 1., 1.],
[ 1., 1.]])
tensor([[ 3., 3.],
[ 3., 3.]])
tensor([[ 27., 27.],
[ 27., 27.]]) tensor(27.)
tensor([[ 4.5000, 4.5000],
[ 4.5000, 4.5000]]) 例2:如果Variable有更多的元素. 需要去指定一个 grad_output 参数, 该参数是一个匹配 shape(形状)的张量.
x =torch.randn(3)
print("=========x=======")
print(x)
x= Variable(x,requires_grad =True)
y=x*x*x
print("========= y= x^3 =======")
print(y)
gradients =torch.FloatTensor([0.1,1.0,0.01])
y.backward(gradients)
print("=========y对x求导 =======")
print(x.grad)
print("=========数学求导=======")
# y=x^3 求导 3x^2,然后乘以权重系数 0.1,1.0,0.01 比较结果
print(3*x*x)计算结果如下,使用pytorch的自动求导,和人工计算导数再乘以权重系数的结果是一样的。
=========x=======
tensor([-1.3326, -0.6574, -2.0749])
========= y= x^3 =======
tensor([-2.3665, -0.2841, -8.9327])
=========y对x求导 =======
tensor([ 0.5327, 1.2965, 0.1292])
=========数学求导=======
tensor([ 5.3275, 1.2965, 12.9155])