11. 字符串
1. 字符串
1.1 字符串的定义
串(String)是由零个或多个字符组成的有限序列,又名叫字符串。一般记为 s =“a1a2a3……an”(n>=0)串可以是空串,即没有字符,直接由 ””表示(注意里边没有空格哦~),或者可以用希腊字母Φ来表示(读fai,四声)。子串与主串,例如“FishC”是“FishC.com”的子串,反之则倒过来。
1.2 字符串的比较
字符串比较大小跟传统的数字比较有点差别,很容易我们可以知道2比1要大,可要是“FishC”和“fishc.com”呢?要怎么比较?比长短?比大小?比大小!没错,比的就是字符串里每个字符的ASCII码大小,因为‘F’== 70 ‘f’== 102,‘f’>‘F’,所以“fishc.com”>“FishC”其实这样的比较大小没有多大意义,字符串的比较我们更重视是否相等!
1.3 字符串的存储结构
字符串的存储结构与线性表相同,也分顺序存储结构和链式存储结构。字符串的顺序存储结构是用一组地址连续的存储单元来存储串中的字符序列的。按照预定义的大小,为每个定义的字符串变量分配一个固定长度的存储区,一般用定长数组来定义。与线性表相似,既然是固定长度的存储区,就存在一个空间分配不灵活的问题,那么会考虑用链式存储结构。
不同的是字符串我们一般都是连在一起表述的,“断章取义”的情况并不多,所以习惯上我们通常还是会直接定义一个足够长度的存储区来存储的。
1.4 字符串的暴力匹配算法
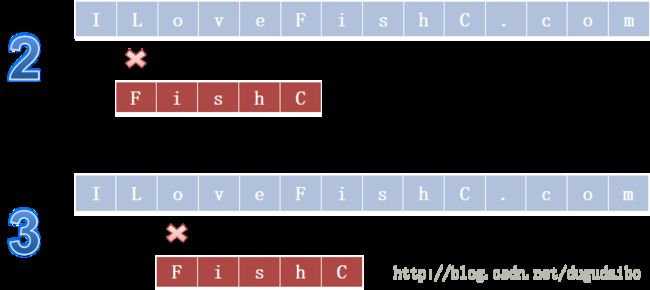
BF(Brute Force)算法属于朴素的模式匹配算法,它的核心思想是:有两个字符串S和T,长度为N和M。首先S[1]和T[1]比较,若相等,则再比较S[2]和T[2],一直到T[M]为止;若S[1]和T[1]不等,则T向右移动一个字符的位置,再依次进行比较。该算法最坏情况下要进行M*(N-M+1)次比较,时间复杂度为O(M*N)。
在这里S是主串,T是子串,这种子串的定位操作通常称作串的模式匹配。假设我们要从主串S=“IloveFishC.com”找到T=“FishC”这个子串的位置,按照BF算法,我们需要进行下边的步骤:


2. KMP 算法
2.1 KMP 算法思想概述
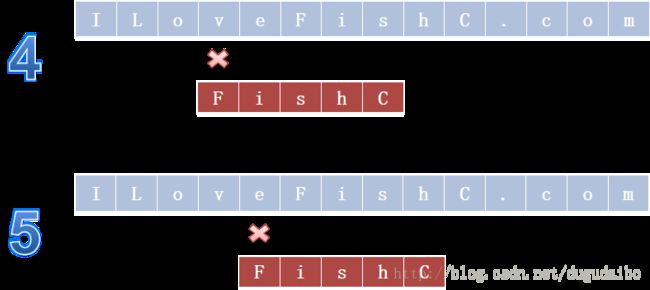
KMP算法是三位老前辈(D.E.Knuth、J.H.Morris 和 V.R.Pratt)的研究结果,大大的避免重复遍历的情况,全称叫做克努特-莫里斯-普拉特算法,简称KMP算法或看毛片算法。上节课我们谈了BF算法,也说了BF算法虽然很黄很暴力,但是效率却不高。我们也给了一个例子。但似乎那个例子不足以反映出导致这种算法效率低下的致命缺陷。因此,我们用下边一个例子来继续探讨:
在上述的这个例子中,如果在匹配的过程中,最后一个字母匹配错误的话,那么就需要将 j 右移一个位置并将上下两个部分进行回溯并重新匹配,这样大大降低了算法的效率。回溯就是坚持条条大路通罗马的决心,然后遇到挫折就回到跌倒的地方重新爬起来,继续往前,这种思想是好的,但效率是低的。
KMP算法的核心就是避免不必要的回溯,那么什么是不必要的呢?问题由模式串决定,不是由目标决定! 下面将给出四个例子对其进行说明。
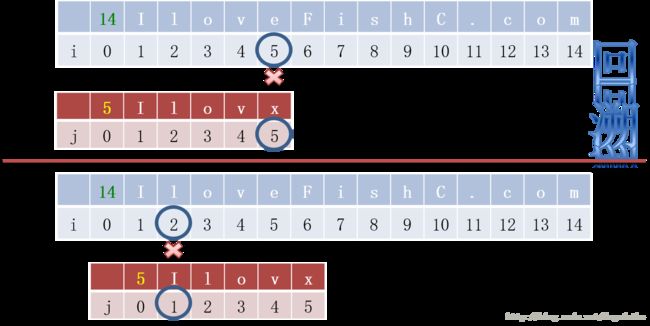
启发思路1:匹配成功的字母之间没有相同的字母。
对于上面的这种情况,我们可以看到 T 中的 1-4 与 S 中的1-4 匹配上了,但是 T 中的 5 与 S 中的 5 没有匹配上。具体来看,因为在 T 中 I≠ l ,但是 T 中的 l 等于 S 中的 l ,所以 T 中的 I 不用再与 S 中的 l 相比较,同理 T 中的 I 不用再与S 中的 o,v 相比较。这个时候需要从 e 开始比较,为不是从 F 开始比较,原因在于 I≠ x , x≠ e ,但是 I 与 e 是什么关系并不清楚,所以这个时候需要从 e 开始比较。
启发思路2:匹配成功的字母之间都是相同的字母。
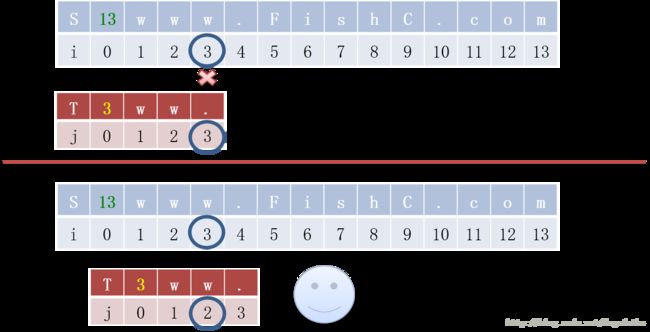
在这个过程中,T 中的情况与思路 1 中 T 的情况是不一样的,思路 1 的 T 中是没有相同的字母的,但是在现在的 T 中是含有相同的字母的。所以现在虽然它们在第三位是不同的,但是不能直接跳到第三位开始比较,因为 T 中的第一位与 S 中的第二位是相同的,所以 T 移动一位之后从第二位开始与 S开始比较。
启发思路3:匹配成功的字母之间有相同的字母,但是不都相同。

在这个过程中,T 中的情况与之前的结果又都不一样了,因为在 T 中 bb 后面肯定接的是 s ,所以下面的 T 移动一个各自肯定是不正确的,他移动 3 个格子之后正好与上面个的 S 对应上了。这个时候我们从 3 号位 s 开始比较,有的人会问为什么从 3 号位开始比较,而不是从 4 号位开始比较。因为我们在第一次比较重只是知道 S 中的 6 号位不想等,就是说他除了不等于 c 还有 25 种与它相等的,所以还需要进行比较。或者从另一个角度考虑,如果 S 中的 6 号位不是 s 还可以直接从 T 的4号位开始比较吗?明显是不可以的。所以从哪个位置开始比较取决于确定相等的位置。
启发思路4:匹配成功的字母之间都是相同的字母。

在这里明显应该往后移 1 位,然后从第 4 位开始比较。
2.2 next 数组
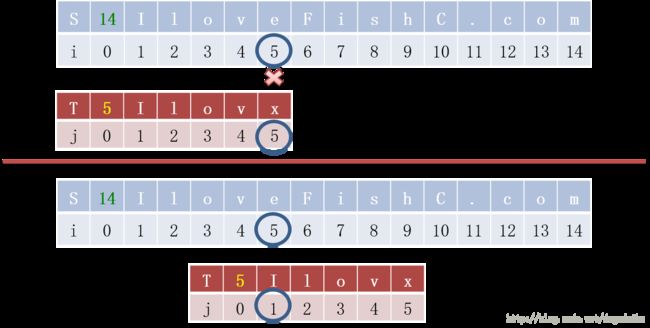
从上面的四个启发过程可以归纳出在使用 KMP 算法过程中使用的 next 数组的形成过程。如下图所示

在这个过程中,假设是在 a 的位置不一样,那么在 S 中不一样的那个位置在下一次匹配中应该与 T 的 0 号位对齐,也就是说直接往下移动一个位置;假设是在 b 的位置不一样,那么在 S 中不一样的那个位置在下一次匹配中应该与 T 的 1 号位对齐;剩下的斗鱼这个过程相似,k 的数值,就是下一次匹配中应该对齐的位置。
确定 k 值得方法是,看它值卡你的数字中前缀与后缀相同得数字有多少,再加上1 。比如说对于最开始的字母 a ,它明显没有前缀和后缀,所以 k 值为0;再看字母 b ,它只有前缀没有后缀,所以是 0+1 = 1;再看字母 a (j = 3),他的前缀为 a ,后缀为 b,所以相等的个数是0,这个时候 k = 0 + 1 =1;再看字母 b (j = 4),他的前缀为 a ,后缀为 a,所以相等的个数是1,这个时候 k = 1 + 1 =2;再看字母 a (j = 5),他的前缀为 ab ,后缀为 ab,所以相等的个数是2,这个时候 k = 2 + 1 =3;再看字母 a (j = 6),他的前缀为 aba ,后缀为 aba,所以相等的个数是3,这个时候 k = 3 + 1 =4;……
2.2.1 next 数组代码原理分析
如下图所示为这个问题的原始表格

可以使用如下的代码进行实现
void get_next( String T, int *next )
{
j = 0;
i = 1;
next[1] = 0;
while( i < T[0] )
{
if( 0==j || T[i] == T[j] )
{
i++;
j++;
next[i] = j;
}
else
{
j = next[j];
}
}
// 因为前缀是固定的,后缀是相对的。
}从 0 开始上述的表格中的数字可以通过该程序得到。
2.3 KMP 算法的实现
KMP 算法的实现的代码如下所示
#include 2.4 KMP 算法的改进
后来有人发现,KMP算法是有缺陷的。比如我们的主串 S =“aaaabcde”,子串 T =“aaaaax”,其中很容易得到next数组为012345。
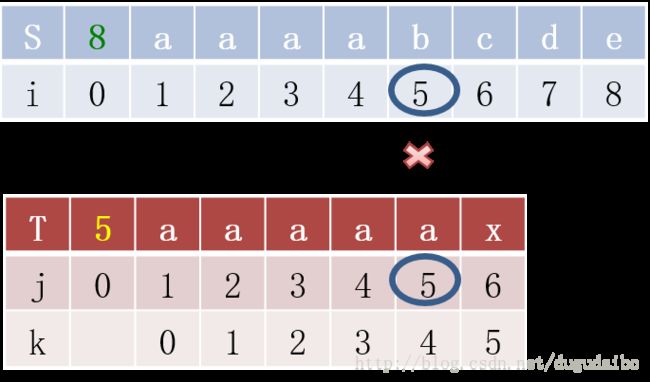
在这里的回溯过程还需要比较 4 3 2 1 这四个位置,但是实际上由于前五个位置的数字都是相等的,所以这个过程是可以省略的,这也就引出了对于KMP 算法的改进。改进后的代码如下
#include 这里面的修改主要是在于 get_next 函数的修改。