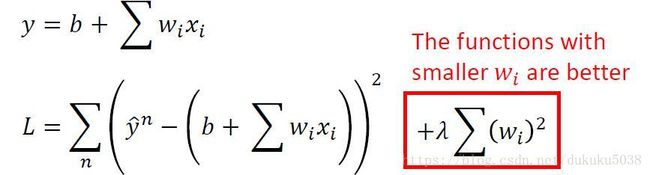机器学习与深度学习系列连载： 第一部分 机器学习（二）监督学习：线性回归
线性回归问题（Linear Regression）
回归问题实际是就是找到一个函数 f ( x ) f(x) f(x)通过输入的数据 x x x，输出一个值 o u t p u t output output。
（本节内容来自 NTU ML2017fall）
应用举例：
- 股市预测
f f f(
) = A 股 指 数 = A 股 指数 =A股指数
-
自动驾驶
f f f(
） = 方 向 盘 的 角 度 = 方向盘的角度 =方向盘的角度 -
商品推荐
f ( 用 户 A ， 商 品 B ) = 购 买 的 可 能 性 （ 购 买 指 数 ） f(用户A，商品B)= 购买的可能性（购买指数） f(用户A，商品B)=购买的可能性（购买指数）
回归问题举例：我们要根据已有的口袋妖怪的攻击力Combat Power（CP），估算出他进化后的攻击力（CP）
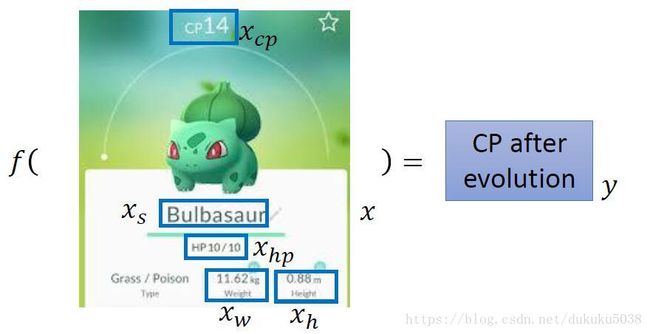
有了问题，我们就可以使用机器学习的方法来解决：
机器学习三板斧
1.设计模型 Model
我们设计线性模型： y ^ = w x c p + b \hat{y}=wx_{cp}+b y^=wxcp+b, x为输入，w为参数，b为偏差（输入数据为10组数据， x c p x_{cp} xcp为不同类型的口袋妖怪，预测进化后的 y ^ \hat{y} y^为攻击值）
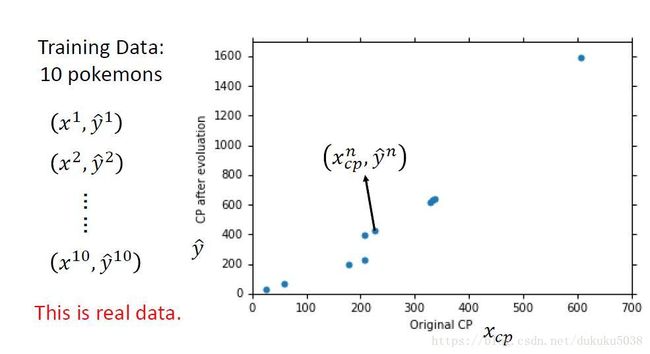
有同学可能要问，为什么是线性模型，非线性模型可以吗。 当然可以，线性模型是最简单的回归问题的例子，我们先拿它开刀。
2. 判断模型好坏 Goodness of function
L o s s = ∑ i = 0 10 ( y ^ − f ( x c p ) ) 2 Loss = \sum_{i=0}^{10}(\hat{y}-f(x_{cp}))^{2} Loss=∑i=010(y^−f(xcp))2
我们找到的函数 f ( x ) f(x) f(x) 在10个训练数据组中预测的结果和真实结果越相近越好，（我们关注的的10个训练数据整体Loss最小，并不是一个数据的loss最小，所以使用累加的方法，将是个数据的loss加起来，形成Loss）也就是说,Loss越小越好，Loss就是我们判断模型好坏的工具
3. 选择最好的函数 pick the best function
选择最好的函数就是 当Loss最小的时候，参数w 和 偏差 b的值，为了求解这个最小的Loss值的时候的w和b，通常线性代数的方法可以求解。（吴恩达CS229中有讲解），在这里，我们使用的是通用方法是梯度下降（机器学习最通用的方法之一）：Gradient Descent（专门章节讲）。
根据高中函数极值的概念，“极大值、极小值”一般在导数为0 的情况：
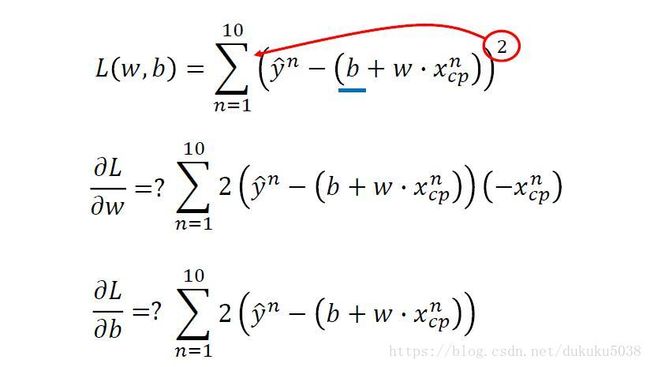
我们随机初始化w和b ，寻找导数为0 的情况（图片中的鞍点和局部最小我们暂时忽略）
η \eta η 为学习率。一般来讲，在导数固定的情况下，学习率越大，w或b变化也就越大。
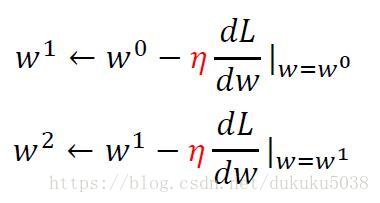
我们得出的Loss 函数的图形表示为下图
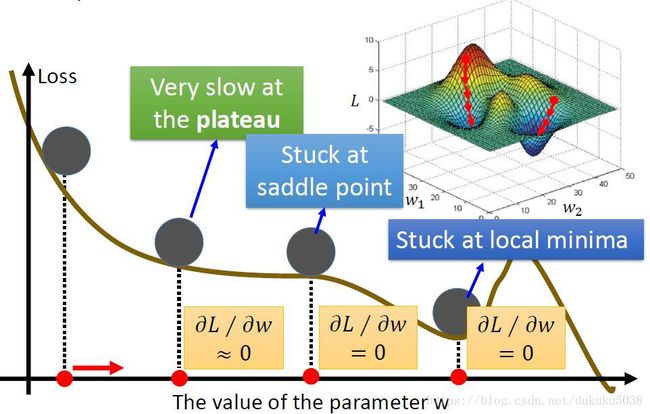
但是寻找最小值的过程不是一帆风顺的，我们有可能会遇到学习很慢（导数接近0）、鞍点（导数为0，但是周围还是有下降空间）、局部最小值（导数为0，但是得到的结果不是整体最小值，而是局部最小值）等问题。但是这些问题都有解决的办法，我们先不考虑。
经过梯度下降，我们选择一个最好的函数（求的的w,b结果为）：
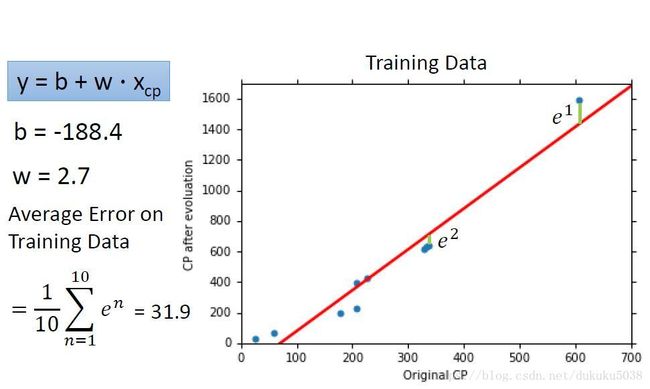
我们将这个问题彻底解决了吗，回到开始我们提出的问题，一定要用线性模型吗? 其他模型可否做的更好？ 接下来，我们使用二次模型，看看结果会不会得到提升。
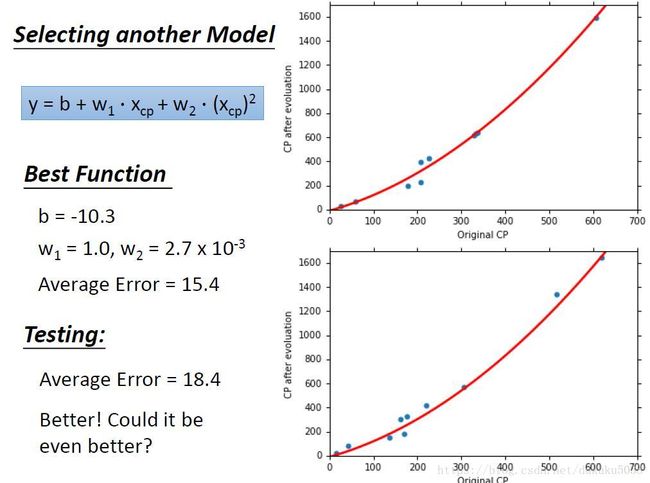
Bingo ! 结果提升了！我们找到的函数是一个平滑的曲线，训练误差几乎少了一半！ 测试误差（在模型没有见过的DATA中）也看起来不错哦。
我们的模型可以更好吗，加上 x c p x_{cp} xcp的指数项是不是越多越好，指数为三次、四次… 更多会不会更好.
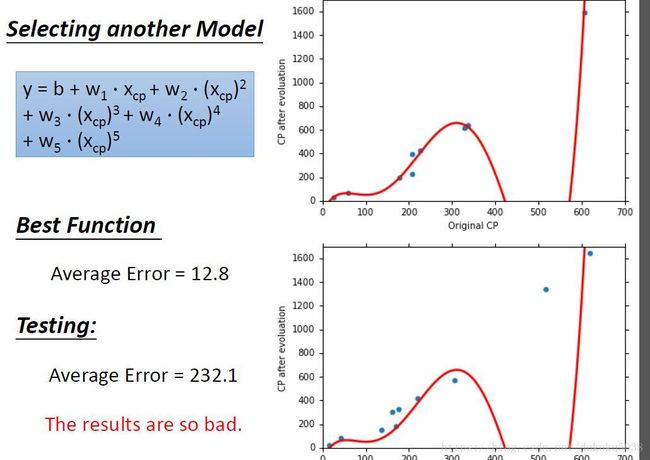
但是结果和直觉刚好相反，现在我们得出了一个过拟合overfitting的概念，就是在训练数据中（模型见过的数据）表现很好，但是在测试数据中表现很差。那我们如何寻找最好的模型呢，即在训练数据中表现的很好，测试数据中也很稳定。 那么我们就人为的实验， x c p x_{cp} xcp的指数的次数1,2,3,4,5。我们发现在指数为3的时候，我们找到的函数是目前最好的。
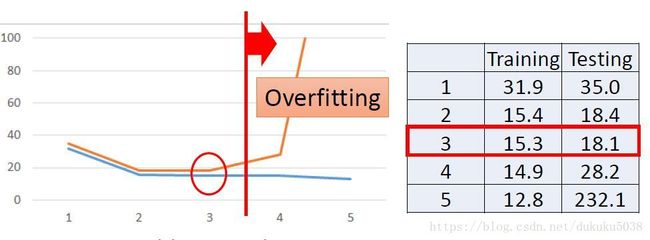
在这里，我们是不是已经解决了这个预测攻击力的问题了呢。
**还没有！**预测攻击力除了考虑精灵的现在的攻击力外，他的身高，体重等等其他维度的信息都没有考虑，理论上，考虑维度越多，得到的结果越准确。（信息论里有证明）
为了得到更加精确的结果，我们需要
- 修改模型，增加数据维度
- 增加正则因子（惩罚因子regularzation）
惩罚因子使得函数更加平滑，让参数w取值更加小，得到的结果更加准确.
那为什么函数w越小，函数就越平滑呢。因为当x变了一个 x + △ x x+ \bigtriangleup x x+△x（一个很小的变化量）的时候，整体的 y = w ∗ x + b y=w*x+b y=w∗x+b 不会变化太大，所以得到的值也更加准确。
而且$\lambda 参 数 的 选 择 ， 也 是 经 过 实 验 得 出 , 我 们 选 择 测 试 结 果 最 好 的 参数的选择，也是经过实验得出, 我们选择测试结果最好的 参数的选择，也是经过实验得出,我们选择测试结果最好的\lambda $， 在这里，测试结果已经达到Loss=11.1 相对于刚才得出的最好结果（选择指数为3次的函数）18.1，又进步了不少。
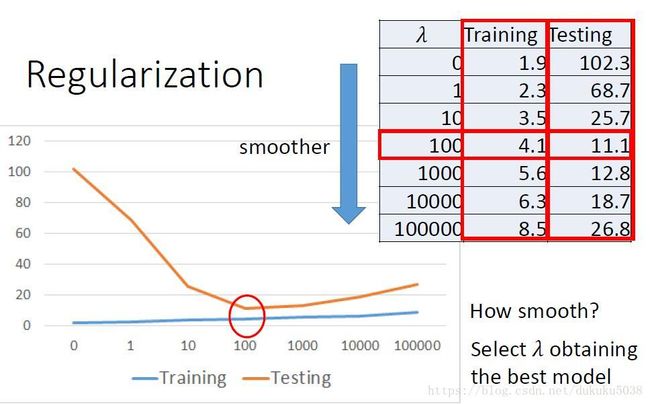
大家现在对回归问题有了一个基本的认识了吧，里面涉及到训练数据（Train）、测试数据（Test）的划分，我将进一步和大家一起学习！
本专栏图片、公式很多来自台湾大学李弘毅老师、斯坦福大学cs229，斯坦福大学cs231n 、斯坦福大学cs224n课程。在这里，感谢这些经典课程，向他们致敬！