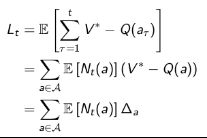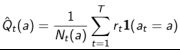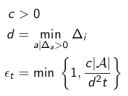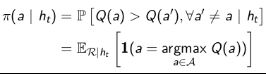机器学习与深度学习系列连载： 第三部分 强化学习（九) 探索与利用

探索与利用

本篇系统的介绍了在强化学习领域如何有效的进行探索，给出了几类探索算法，通过引入后悔值，借助多臂赌博机这一与状态无关的示例从理论上论述了相关算法的有效性，随后很简单地介绍了将其扩展至与状态相关学习问题和这些算法如何具体应用于解决MDP问题。

1. 简介 Introduction

探索和利用的困局：

• 利用是做出当前信息下的最佳决定，
• 探索则是尝试不同的行为继而收集更多的信息。最好的长期战略通常包含一些牺牲短期利益举措。通过搜集更多或者说足够多的信息使得个体能够达到宏观上的最佳策略。

因此探索和利用是一对矛盾。

几个基本的探索方法：

朴素探索(Naive Exploration): 在贪婪搜索的基础上增加一个Ɛ以实现朴素探索；

几个基本的探索方法：

朴素探索(Naive Exploration): 在贪婪搜索的基础上增加一个Ɛ以实现朴素探索；

乐观初始估计(Optimistic Initialization): 优先选择当前被认为是最高价值的行为，除非新信息的获取推翻了该行为具有最高价值这一认知；

概率匹配（Probability Matching): 根据当前估计的概率分布采样行为；

信息状态搜索(Information State Search): 将已探索的信息作为状态的一部分联合个体的状态组成新的状态，以新状态为基础进行前向探索。

根据搜索过程中使用的数据结构，可以将搜索分为：

• 依据状态行为空间的探索(State-Action Exploration)
• 参数化搜索（Parameter Exploration)

前者指针对每一个当前的状态，以一定的算法尝试之前该状态下没有尝试过的行为。

后者则直接针对策略的函数近似，此时策略用各种形式的参数表达，探索即表现为尝试不同的参数设置。

• 后者的优点是：得到基于某一策略的一段持续性的行为；
• 其缺点是对个体曾经到过的状态空间毫无记忆，也就是个体也许会进入一个之前曾经进入过的状态而并不知道其曾到过该状态，不能利用已经到过这个状态这个信息。

2. 与状态无关的多臂赌博机 Multi-Armed Bandits

多臂赌博机（下图）是由多个独立的单臂赌博机构成，赌博机相当于环境，个体拉下某一单臂赌博机的拉杆表示选择该赌博机，随后该赌博机会给出一个即时奖励R。各个单臂赌博机之间是独立无关的，这等于说各单臂赌博机所给出的即时奖励值无关且各自的奖励分布也不同。此外，同一时刻只能拉下其中一个赌博机的拉杆，在某一个赌博机上先前拉杆得到的奖励与随后拉杆所能得到的奖励无关。另外，多臂赌博机每给出一个即时奖励，该Episode随即结束，因此一个Episode就是由一个行为和一个即时奖励构成，与状态无关。

由上文的描述可以得出，多臂赌博机可以看成是由行为空间和奖励组成的元组 ，假如一个多臂赌博机由 m 个单臂赌博机组成，那么行为空间将由 m 个具体行为组成，每一个行为对应拉下某一个单臂赌博机的拉杆。在 t 时刻，个体从行为空间 A 中选择一个行为 $a_t$ , 随后环境产生一个即时奖励 $r_t$ 。采取行为a得到的即时奖励 r 服从一个个体未知的概率分布： $R^a(r)=P[r|a]$ 中采样得到。个体可以持续的与多臂赌博机进行交互。

问题：利用得到的即时奖励值，个体使用如何的搜索策略可以最大化其累及即时奖励：

为了方便描述问题，我们先给出几个定义： A

这个问题不涉及状态本身，我们仿照状态价值（或状态行为价值）的定义来定义一个仅针对某一行为的价值Q(a)：

它的意思是一个行为的价值等于该行为能得到的即时奖励期望，即该行为得到的所有即时奖励的平均值。

假如我们能够事先知道哪一个单臂赌博机能够给出最大即时奖励，那我们可以每次只选择对应的那个拉杆。如果用 $V^{\ast }$ 表示这个最优价值， $a^{\ast }$ 表示能够带来最优价值的行为，那么：

事实上我们不可能事先知道拉下哪个拉杆能带来最高奖励，因此每一次拉杆获得的即时奖励可能都与最优价值V*存在一定的差距，我们定义这个差距为后悔值(regret):

每做出一个行为，都会产生一个后悔值 l_t ，因此随着持续的拉杆行为，将所有的后悔值加起来，形成总后悔值：

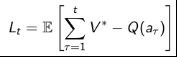
这样，最大化累计奖励的问题就可以转化为最小化总后悔值了。

注：之所以这样转换，是为了描述问题的方便，在随后的讲解中可以看到，较好的算法可以控制后悔值的增加速度。而用最大化累计奖励描述问题不够方便直观。

现在我们从另一个角度重写总后悔值。定义计数 $N_t(a)$ 为到 t 时刻时已执行行为 A 的次数。定义差距 $\Delta$ a 为最优价值 $a^{\ast }$ 与行为a的价值之间的差。那么总后悔值可以推导成：

这相当于把个行为的差距与该行为发生的次数乘起来，随后把行为空间的所有行为的这个乘积再相加得到，只不过这里是期望。

把总后悔值用计数和差距描述可以使我们理解到一个好的算法应该尽量减少那些差距较大的行为的次数。不过我们并不知道这个差距具体是多少，因为根据定义虽然最优价值 V^* 和每个行为的差距 \Delta a 都是静态的，但我们并不清楚这两者的具体数值，我们所能使用的信息就是每次行为带来的即时奖励 r 。那么我们如何利用每次行为的即时奖励呢？

我们使用每次的即时奖励来计算得到 t 时刻止某一行为的平均价值：

这个方法也叫蒙特卡罗评估，以此来近似该行为的实际价值 Q(a)

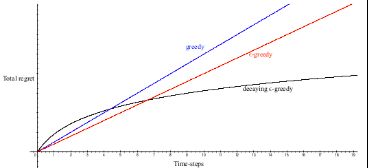
我们先直观了解下不同形式的随机策略其总后悔值随着时间的变化曲线：

对于Ɛ-greedy探索方法，总后悔值会呈线性增长，这是一个好的算法所不能接受的。这是因为每一个时间步，该探索方法有一定的几率选择最优行为，但同样也有一个固定小的几率采取完全随机的行为，如采取随机行为，那将一直会带来一定后悔值，如果持续以虽小但却固定的几率采取随机行为，那么总的后悔值会一直递增，导致呈现与时间之间的线性关系。类似的softmax探索方法与此类似。

对于greedy探索方法，其总后悔值也是线性的，这是因为该探索方法的行为选择可能会锁死在一个不是最佳的行为上。

现在问题是，能否找到一种探索方法，使用该探索方法时随着时间的推移其总后悔值增加得越来越少呢？答案是肯定的。下文将依次介绍几种较好的探索方法。

2. 估计方法

(1) 乐观初始估计(Optimistic Initialization)

理论上，这仍是总后悔值线性增加的探索方法，但是实际应用效果却非常好，因此放在这里介绍。其主要思想是在初始时给行为 A 一个较高的价值，随后使用递增蒙特卡罗评估来更新该行为的价值：

可以看出，某行为的价值会随着实际获得的即时奖励在初始设置的较高价值基础上不断得到更新，这在一定程度上达到了尽可能尝试所有可能的行为。但是该方法仍然可能锁死在次优行为上。理论上，该方法与greedy或Ɛ-greedy结合带来的结果同样是线性增加的总后悔值。

(2) 衰减Ɛ-greedy(Decaying Ɛ-greedy)
这是在Ɛ-greedy的基础上做细小的修改，这个在之前讲解过：即随着时间的延长， \epsilon 值越来越小。我们来从理论上考虑如下这个安排：

假设我们现在知道每一个行为的最优价值 $V^{\ast }$ ，那么我们可以根据行为的价值计算出所有行为的差距 ${\Delta }_a$ 。可设置为：如果一个行为的差距越小，则尝试该行为的机会越多；如果一个行为的差距越大，则尝试该行为的几率越小。数学表达如下：

按照上述公式设定的Ɛ-greedy方法是一种衰减Ɛ-greedy方法，惊奇的是它能够使得总的后悔值呈现出与时间步长的次线性（sublinear）关系：对数关系。不巧的是，该方法需要事先知道每个行为的差距 ${\Delta }_a$ ，实际上式不可行的。后续的任务就是要找一个实践可行的总后悔值与时间步长呈对数关系的探索方法。

(2) 不确定行为优先探索(optimism in the face of uncertainty)

在展开该方法之前，先思考一个问题：试想一下怎样的多臂赌博机问题容易选择最好行为？如果一个多臂赌博机其中某个单臂一直给以较高的奖励，而另一个（或其它）单臂则一直给出相对较低的奖励，那么选择起来就容易得多了。相反，如果多个单臂给出的奖励变异程度较大，忽高忽低，而且多个单臂给出的奖励值有很多时候非常接近，那么选择一个价值高的行为可能就要花费很长时间了，也就是说这些单臂给出的奖励虽然类似，但其均值却差距较大。因此，可以通过比较两个单臂价值（均值）的差距∆以及描述其奖励分布的相似程度的KL散度 $KL(R_a||R_{a^{\ast }})$ 来判断总的后悔值下限：差距越大，后悔值越大；奖励分布的相似程度越高，后悔值越低。

针对多臂赌博机，有一个定理是这样说的：存在一个总后悔值的下限，没有哪一个算法能够做得比这个下限更好：

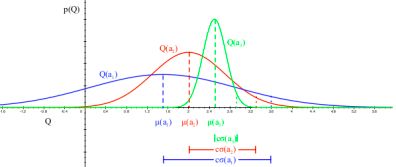
现在我们来看看不确定行为优先搜索具体是怎么回事。想象一下现在由3个不同的单臂组成的多臂赌博机，现根据历史行为和奖励信息，绘制它们当前的奖励分布图。

特别注意这并不一定是它们真正服从的奖励分布，而是个体根据历史信息构建的一个经验分布。现在问题是，接下来该如何选择哪一个行为？正确的行为是采取蓝色的单臂，而不是绿色的单臂。理由是，蓝色的分布虽然其奖励均值比绿色的低（图中相应曲线最大P值对应的Q值），但其实际奖励分布范围较广，由于探索次数的限制，蓝色单臂对应的行为价值有不少的几率要比分布较窄的绿色单臂要高，也就是说蓝色单臂的行为价值具有较高的不确定性。因此我们需要优先尝试更多的蓝色单臂，以更准确地估计其行为价值，即尽可能缩小其奖励分布的方差。

从上面的分析可以看出，单纯用行为的奖励均值作为行为价值的估计进而知道后续行为的选择因为采样数量的原因可能会不够准确，更加准确的办法是估计行为价值在一定可信度上的价值上限，比如可以设置一个行为价值95%的可信区间上限，将其作为指导后续行为的参考。如此一个行为的价值将有较高的可信度不高于某一个值：

下图针对红色行为的价值曲线标示了该不等式右侧的两个横坐标变量的位置（或范围）：

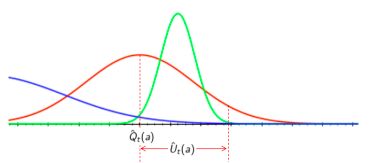
由此可以理解，当某一行为的计数较少时，该行为价值某一可信度上的价值上限将偏离均值较多；随着针对某一行为的奖励数据越来越多，该行为价值在某一可信度的上限将越来越接近均值。我们可以用置信区间上界(Upper Confidence Bound, UCB)来指导行为的选择，令：

如果即时奖励分布是明确可知的，那么置信区间上界将比较容易根据均值进行求解。例如对于高斯分布95%的置信区间上界是均值与两倍标准差的和。而一般的对于分布未知的执行区间上界如何得到呢？

该定理给出了位于区间[0,1]的两两随机变量其期望与均值之间满足的关系。结合该不等式，很容易得到:

该不等式描述的置信区间上限较之前描述的置信区间上限较弱，但也是实际可用的不等式。利用该不等式得到一个特定可信度的置信区间上限就比较容易了。假定我们设定行为的价值有p的概率超过我们设置的可信区间上界，即令

那么可以得到：

随着时间步长的增加，我们逐渐减少 p 值，比如 $p=t^{-4}$ ，那么随着时间步长趋向无穷大，我们据此可以得到最佳行为。

给出实际应用时 $U_t(a)$ 和 $a_t$ 的公式：

注：上式中，argmax是针对后两项整体的，式中 N_t(a) 是行为a的计数、 Q(a) 是根据历史数据获得的奖励的平均值。

结论：由UCB算法设计的探索方法可以使得总后悔值满足对数渐进关系。

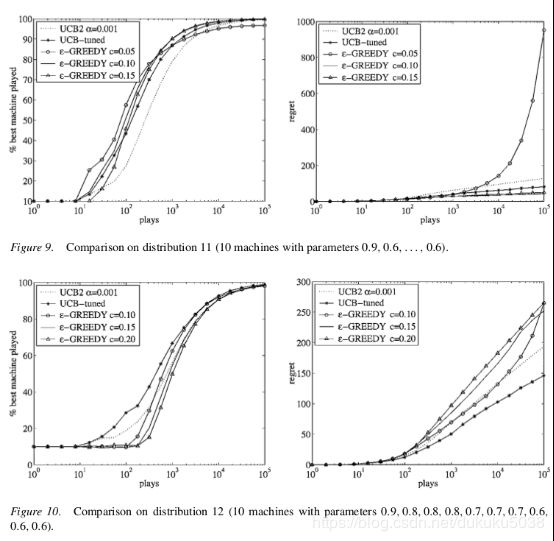
下图展示了不同设置的UCB算法和不同设置的Ɛ-greedy算法在10臂赌博机上的表现情况。该图由四个分图组成，上方与下方的不同在于10-臂赌博机各臂参数设置不同，相当于描述了各个单臂的即时奖励的分布。左侧图描述的是各个算法随时间表现，右侧图描述的是总后悔值随时间的变化。

事实表明，Ɛ-greedy算法如果参数调整得当，可以表现的很好，反之则可能是灾难。UCB在没有掌握任何信息的前提下也能做得很好。

前文降到了UCB算法可以得到很好的效果，UCB算法仅仅依靠统计各个行为的奖励均值和出现的次数，并在此基础上设定一定的置信区间上节，指导行为选择。如果我们利用历史信息构建即时奖励针对每个行为的分布情况，在此基础上决定后续行为的选择也是一条可行的办法。

假设各单臂赌博机服从相互独立的高斯分布，可以用每一个单臂赌博机的均值和标准差参数化整体奖励分布：

选择均值和一定比例的标准差之和来作为UCB算法中的置信区间上限，即依据下式选择后续行为：

注：上式中，argmax是针对后两项整体的

(3) 概率匹配 Probability Matching

概率匹配的想法先估计每一个行为可能是最佳行为的概率，然后依据这个概率来选择后续行为。

该算法背后隐藏的思想是：越不确定价值的行为有着越高的几率被选择，这种被选择的目的是通过采样减少其不确定性，进而调整后续策略。

Thompson sampling算法是基于该思想的一种实际可行的算法，该算法实现起来非常简单，同时也是一个非常接近总后悔值对数关系的一个算法。该算法的步骤如下：

1. 利用历史信息构建各单臂的奖励分布估计

2. 依次从每一个分布中采样得到所有行为对应即时奖励的采样值

3. 选取最大采样值对应的行为。

该算法的采样过程中利用到了历史信息得到的分布，同时行为得到的真实奖励值将更新该行为的分布估计。

(4) 信息价值 Value of Information

本小节尝试从信息的角度来讲解另外一种探索方法。探索之所以有价值是因为它会带来更多的信息，那么能否量化被探索信息的价值和探索本身的开销，以此来决定是否有探索该信息的必要呢？这就涉及到信息本身的价值。

先打个比方，对于一个2臂赌博机。假如个体当前对行为a1的价值有一个较为准确的估计，比如是100镑，这意味着执行行为a可以得到的即时奖励的期望，个体虽然对于行为a2的价值也有一个估计，假如说是70镑，但这个数字非常不准确，因为个体仅执行了非常少次的行为a2。那么获取“较为准确的行为a2的价值”这条信息的价值有多少呢？这取决于很多因素，其中之一就是个体有没有足够多的行为次数来获取累计奖励，假如个体只有非常有限的行为次数，那么个体可能会倾向于保守的选择a1而不去通过探索行为a2而得到较为准确的行为a2的价值。因为探索本身会带来一定几率的后悔。相反如果个体有数千次的行为次数，那么得到一个更准确的行为a2的价值就显得非常必要了，因为即使通过一定次数的探索a2，后悔值也是可控的。而一旦得到的行为a2的价值超过a1，则将影响后续数千次的行为的选择。

为了能够确定信息本身的价值，可以设计一个MDP，将信息作为MDP的状态构建对其价值的估计：

继续使用2臂赌博机的例子来解释信息状态的内容。在这个例子中，一个信息状态对应于分别采取了行为a1和a2的次数，例如S0<5,3>可以表示一个信息状态，它意味着个体在这个状态时已经对行为a1执行了5次，a2执行了3次。随后个体又执行了一个行为a1，那么状态转移至S1<6,3>。事实上这样的信息状态构建得到的MDP是一个规模非常庞大的MDP，解决它需要使用之前将结果的函数近似。

我们再举一个例子来更加清楚的解释信息状态是如何转换以及转换概率是如何计算的。

现在考虑一个即时奖励服从伯努利分布的赌博机，或者一个服从伯努利分布的药物实验：

上式中 ${\mu }_a$ 是拉下一个拉杆能够获得奖励1的概率，或者是选择一个药物其疗效超过一定预期的概率。对于由服从该分布的单臂赌博机构成的2臂赌博机，我们的目标就是找到哪一个赌博机有较高的 ${\mu }_a$ ，这样就能每次选择那个较高 ${\mu }_a$ 的赌博机，以此来最小化总后悔值。如果是药物实验，则可以想象成是比较两种药物的疗效优劣，已决定后续选择的药物。

对于这样由2个行为组成的行为空间，可以将信息状态描述为 $s<\alpha ,\beta >$ ，其中 ${\alpha }_a$ 为执行行为 A 得到奖励为0的次数，其中 ${\beta }_a$ 执行行为 A 得到奖励为1的次数。该信息状态的内容记载了所有历史信息。

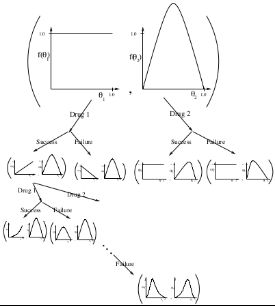
下图是较为直观的信息状态转移图。我们从药物实验的角度来解释，行为a1表示个体对某一患者使用药物a1，假设疗效服从伯努利分布，它与一个金标准比较可以是只有2个：优于金标准和不优于金标准。最初个体对于药物a1的疗效一无所知，即它并不清楚药物a1优于金标准疗效的概率分布，也就是说从0-1之间任意一个概率都是均一的（图中上方括号左侧的水平线图）；而对于药物a2，个体通过实验了解到其平均有50%的概率优于金标准疗效（途中上方括号右侧的曲线图）。每一个信息状态对应的两个曲线图都是对当前状态所有历史信息的描述，也就是各药物疗效优于或不优于金标准的计数。现在前向观察这个搜索树，比如现在选择了行为a1，发现行为a1的疗效要优于金标准，那么我们修改对行为a1疗效的计数，同时反映在对应的图上。如果随后继续使用a1但发现疗效不好，则目前对于a1来说一次疗效好，一次不好。则总体呈现出50%类似于药物a2的疗效。

3. 小结

至此通过与状态无关的例子讲解了几大类探索方法。其中特别要指出的是对不确定优先探索这类方法应用在工业上有一定的危险性。因为这类算法优先尝试那些不确定的行为，而一些不确定的行为在工业应用上可能并不安全。例如控制一个机器人行走，你可能并不想让其一直探索未知的行为，这可能导致其摔倒或者其它不可预知的不好后果。

本专栏图片、公式很多来自David Silver主讲的UCL-Course强化学习视频公开课和台湾大学李宏毅老师的深度强化学习课程,在这里，感谢这些经典课程，向他们致敬！