《剑指offer》----查找/排序/递归/循环/位操作专题
重点: 二分查找 快速排序 归并排序
查找: 顺序查找 二分查找 哈希表查找 二叉树查找
面试题:
/**
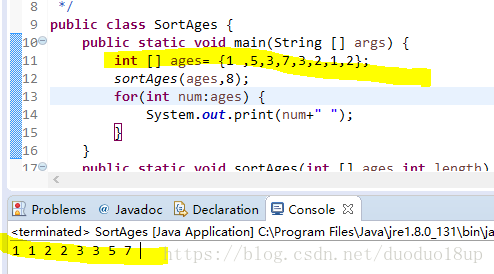
* 思路:就是有一个原始的ages[] 数组 ,但是没有排顺序,我们借助一个新数组timesOfAges[] 对年龄进行次数统计
* 然后 按照年龄大小 分别存入对应次数的ages 即相当于排序
* 例子: 原数组 {1 ,5,3,7,3,2,1,2} ------->{1,1,2,2,3,3,5,7}
* @author 多多
*
*/public static void sortAges(int [] ages,int length) {
if(ages==null || length<=0)
return;
int oldAge=99; //最大年龄规定为99
int[] timesOfAges=new int[oldAge+1];
//初始化次数均为0
for(int i=0;i oldAge || age<0) {
throw new RuntimeException("输入错误的年龄,请重新输入");
}else {
timesOfAges[age]++; //以年龄为数组下标 对应值储存年龄次数
}
}
int count=0; //统计次数
//对原始数组排序 即按照年龄顺序 输入对应次数个年龄到ages数组中
for(int i=0;i<=oldAge;i++) {
for(int j=0;j 结果测试:
异常结果测试:
NOTE:给出的所有元素都大于0,若数组大小为0,请返回-1。
考虑特例1:没有移动 即数据本身(第一个数字即最小)
解决方法: middle的初始位置设为begin
考虑特例2:两个下标指向数字和中间数字均相同 无法分清楚属于哪个数组
解决方法:
public int minNumberInRotateArray(int [] array) {
if(array==null || array.length==0)
return -1; int begin=0;
int end=array.length-1;
int indexMid=begin; //考虑数组本身的情况(最小值即为begin位置值)
while(array[begin]>= array[end]){
if(begin==end-1){ //已经相邻 则取第二个指针指向的值
indexMid=end;
break;
}
indexMid=(begin+end)/2; //求中值位置
//特例2出现(三个值均相同 用顺序查找 找到最小值返回)
if(array[indexMid]==array[begin] && array[indexMid]==array[end])
return minInOrder(array,begin,end);
if(array[indexMid] >= array[begin]){ //中值元素>第一个指针的值 (在大数的子数组中) 最小值 肯定在右边
begin=indexMid; //第一个指针移到中值位置
}else if(array[indexMid] <= array[end]){ // 中值元素<第二个指针的值 (在小数的子数组中) 最小值 肯定在左边
end=indexMid; //第二个指针移到中值位置
}
}
return array[indexMid]; //返回第二个指针指向的值
}
//特例2出现处理函数(三个值均相同 用顺序查找 找到最小值返回)
public int minInOrder (int [] array,int begin,int end){
int result=array[begin];
for(int i=begin+1;i<=end;i++){
if(result> array[i])
result=array[i];
}
return result;
}
}时间复杂度:二分查找O(logn)
其他想法:
mid = low + (high - low)/2
需要考虑三种情况:
(1)array[mid] > array[high]:
出现这种情况的array类似[3,4,5,6,0,1,2],此时最小数字一定在mid的右边。
low = mid + 1
(2)array[mid] == array[high]:
出现这种情况的array类似 [1,0,1,1,1] 或者[1,1,1,0,1],此时最小数字不好判断在mid左边
还是右边,这时只好一个一个试 ,
high = high - 1
(3)array[mid] < array[high]:
出现这种情况的array类似[2,2,3,4,5,6,6],此时最小数字一定就是array[mid]或者在mid的左
边。因为右边必然都是递增的。
high = mid
注意这里有个坑:如果待查询的范围最后只剩两个数,那么mid 一定会指向下标靠前的数字
比如 array = [4,6]
array[low] = 4 ;array[mid] = 4 ; array[high] = 6 ;
如果high = mid - 1,就会产生错误, 因此high = mid
但情形(1)中low = mid + 1就不会错误
public class Solution {
public int minNumberInRotateArray(int [] array) {
int low = 0 ; int high = array.length - 1;
while(low < high){
int mid = low + (high - low) / 2;
if(array[mid] > array[high]){
low = mid + 1;
}else if(array[mid] == array[high]){
high = high - 1;
}else{
high = mid;
}
}
return array[low];
}
}递归:
问题出现: 多个节点重复 ,且重复节点数会随着n的增大急剧增加 ,时间复杂度以n的指数方式递增。
public static long Fibonacci(int n) { //输出第n项数字
int [] result= {0,1}; //初始结果数组
if(n<2)
return result[n];
long fibMinusOne=1; //记录第n-1项数字
long fibMinusTwo=0; //记录前n-2项数字
long fibN=0; //第n项数字的值
for(int i=2;i<=n;i++) {
fibN=fibMinusOne+fibMinusTwo;
fibMinusTwo=fibMinusOne; //每回计算完则平移
fibMinusOne=fibN;
}
return fibN;
}计算复杂度为 O(n)
斐波那契数列相关应用问题(青蛙上台阶):
思路:
| 1, (n=1)
f(n) = | 2, (n=2)
| f(n-1)+f(n-2) ,(n>2,n为整数)
Note: 初始值从1开始
public class Solution {
public int JumpFloor(int target) {
if(target<=0)
return 0;
if(target==1)
return 1;
if(target==2)
return 2;
int FibOne=2;
int FibTwo=1;
int FibN=0;;
for(int i=3;i<=target;i++){
FibN=FibOne+FibTwo;
FibTwo=FibOne;
FibOne=FibN;
}
return FibN;
}
}
变态跳台阶:
思路1:
因为n级台阶,第一步有n种跳法:跳1级、跳2级、到跳n级
跳1级,剩下n-1级,则剩下跳法是f(n-1)跳2级,剩下n-2级,则剩下跳法是f(n-2)
所以f(n)=f(n-1)+f(n-2)+...+f(1)
因为f(n-1)=f(n-2)+f(n-3)+...+f(1)
所以f(n)=2*f(n-1)
等比数列的规律------------f(n)=2^(n-1)
思路2 :
每个台阶都有跳与不跳两种情况(除了最后一个台阶),最后一个台阶必须跳。所以共用2^(n-1)中情况
public class Solution {
public int JumpFloorII(int target) {
return 1<<(target-1); //即 2^(n-1)
}
}矩形覆盖问题:
题目:
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
public class Solution {
public int RectCover(int target) {
//target=1 方法1
if(target<=0)
return 0; //注意没有方法则返回0
if(target==1)
return 1;
if(target==2)
return 2;
int one=2;
int two=1;
int Fib=0;
for(int i=3;i<=target;i++){
Fib=one+two;
two=one;
one=Fib;
}
return Fib;
}
}位运算
public class Solution {
public int NumberOf1(int n) {
int count=0;
while(n!=0){
if((n&1)==1) //判断每一位是否为1
count++;
n>>=1; //数字二进制表示不断右移一位
}
return count;
}
}分析:
思想:用1(1自身左移运算)和n的每位进行位与,来判断1的个数
public class Solution {
public int NumberOf1(int n) {
int count=0;
int flag=1;
while(flag!=0){
if((n& flag)!=0) //和flag位与 不为0 说明次低位为1
count++;
flag<<=1; //flag不断左移 匹配数字的位数
}
return count;时间复杂度: 循环次数=整数二进制表示位数 32位
public class Solution {
public int NumberOf1(int n) {
int count=0;
while(n!=0){ //有多少个1就能进行多少次这样的操作
n=n&(n-1);
count++;
}
return count;题目1:
//判断一个数是不是2的整数次方public static boolean isPower(int n){
if(n<1) return false;
int m=n&n-1; //只有一个1 所以做一次此操作之后即为0
return m==0;
}//常规做法 1<<=1 总会移动至和给定数字相同public static boolean isPower(int n){
if(n<1) return false;
int i=1;
while(i<=n) {
if(i==n)
return true;
i<<=1;
}
return false;
}
public static int changeAtoB(int A,int B) {
int count=0;
int C=A^B; //先将输入的两个数字进行异或 即知道不同位数的二进制表示
while(C!=0) { //统计异或结果中1的个数
count++;
C=C&(C-1);
}
return count;
}