1.学习总结(2分)
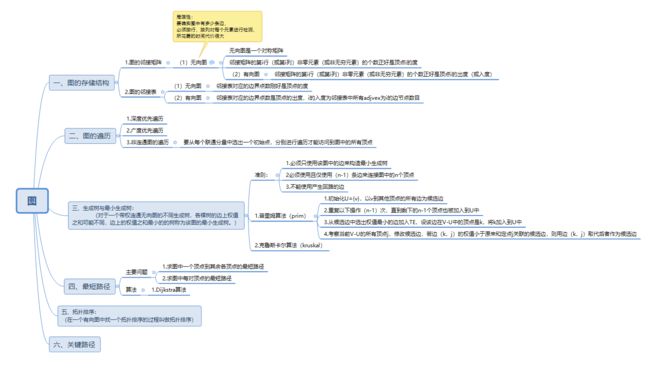
1.1图的思维导图
1.2 图结构学习体会
谈谈你对图结构中的几个经典算法学习体会。具体有：
- 深度遍历算法
基本是完成6-1，6-2之后的题目有用到这些算法的就直接复制粘贴，所以就了还是有点忘记的，还是需要复习.. - 广度遍历算法
同上。。 - Prim和Kruscal算法
相对于kruskal，我比较常用prim算法来解决最小生成树问题，像7-4和7-5，其实对于代码还是有些不理解lowcost和closest数组的作用，主要的理解是通过P227中对prim算法过程的图解，感觉相对于prim的树是逐渐从初始顶点开始的算法相比，kruskal算法是先形成各个树的枝干然后再连接成树的过程会比较麻烦 - Dijkstra算法
对于这个算法的应用，目前我只是在课堂派用S、U、V画图表示过过程， - 拓扑排序算法
对于拓扑排序算法，针对6-3，我将其分为了六部分记忆：
1.入度初始化为0
2.遍历统计各顶点入度
3.将入度为0的顶点入栈
4.进行拓扑排序，以栈内有元素为循环条件，以栈内元素的顺序进行遍历，访问过的端点将其入度减一，若为0则将其入栈，并统计入栈端点数量，并将栈内访问过邻接顶点的顶点入数组
5.通过入栈端点数量是否等于端点数判断是否有回路
6.输出
感觉分成了六部分之后挺好记忆的
2.PTA实验作业（4分）
2.1 题目1：7-3 六度空间
2.2 设计思路
主函数中应用函数的代码：
for i=0 to i=顶点数，遍历每一个顶点
{
for i=0 to i=顶点数
初始化visited[i]等于0，即每一个顶点都没有被访问过
应用函数计算当前节点的六度结果BFS（i）；
}
void BFS(int v)：
定义 整型变量level 表示当前遍历的节点与该节点的距离，
tail存储上一个距离的最后一个节点；
last存储当前距离的最后一个节点，初始化为当前节点v；
count表示所遍历的节点数量；
x表示当前遍历的节点；
定义 队列 Q；
v进队列，并将v节点标记为已访问
while（队列Q不空）{
x等于 队头元素；
将队头元素出队；
for i=0 to i 等于顶点数 ，共遍历所有顶点
{ if (顶点i与x有联系，且顶点i未被访问)
{ 节点i进队
标记i已访问；
count数量加一；
tail 等于 i;
}end if
}end for
if（当前顶点是上一距离的最后一个节点，即x等于last）
{ 更新当前距离的最后一个节点last等于tail；
距离level加一；
}end if；
if（距离等于6）
跳出循环；
}
则count就是传参v距离不超过6的结点数；
例子：如下图节点关系
last初始化等于v；
v=1，进队
队不为空
x等于队头1
tail 依次等于 2,3
此时 x等于last等于1
所以 更新last等于tail等于3
x依次等于队头 2,3
所以tail依次等于 4,5 6,7
此时x等于last等于3
所以更新last等于7
就这样一层一层地遍历，统计每层的数量，直到第六层。
2.3 代码截图
1.主函数
2.该题函数
2.4 PTA提交列表说明。
错误：.段错误
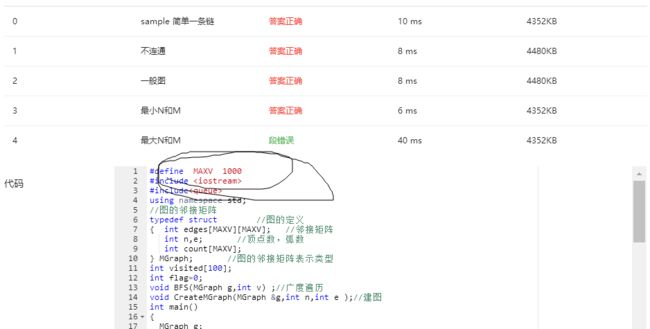
题目要求的顶点范围是
，所以定义MAXV为10001，但是这样的话就会全部段错误
最后不用结构体，直接用全局数组，就可以通过了。
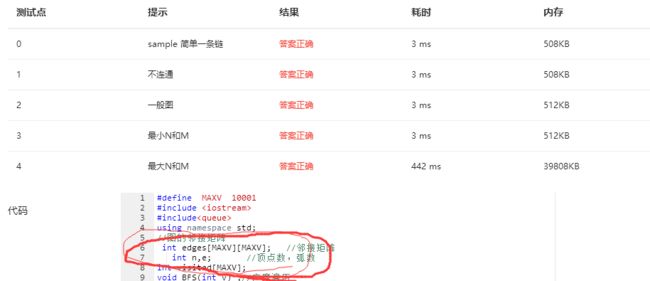
具体百度好像挺复杂的，注意到我们之前好像有讲过的一点，就是 结构体要求：结构体的总大小为结构体最宽基本类型成员大小的整数倍，如有需要编译器会在最末一个成员之后加上填充字节（trailing padding）。.不知道是不是因为这样，结构体所需内存比数组大，因而段错误。
2.1 题目2：题目名称：7-1 图着色问题
2.2 设计思路
主要思路
利用flag的值判断输出内容
判断主要有两个不符合条件：
1.颜色数量与题目要求不等
2.临点颜色不同定义整型全局变量flag=1；
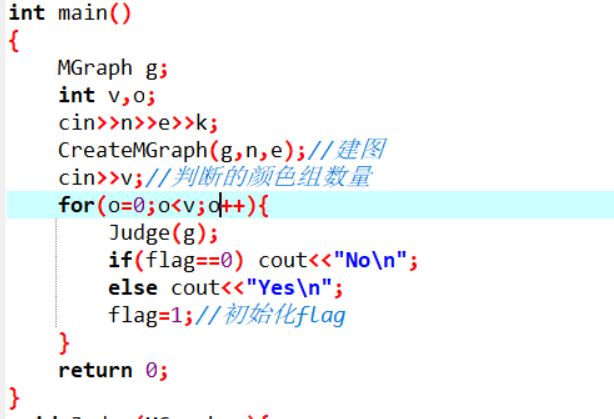
主函数（部分）
for i=0 to i=v 共v次进行判断{
引用函数Judge(传参 图g)进行判断;
if(flag等于0)
cout<<"No\n";
否则
cout<<"Yes\n";
初始化flag 等于1
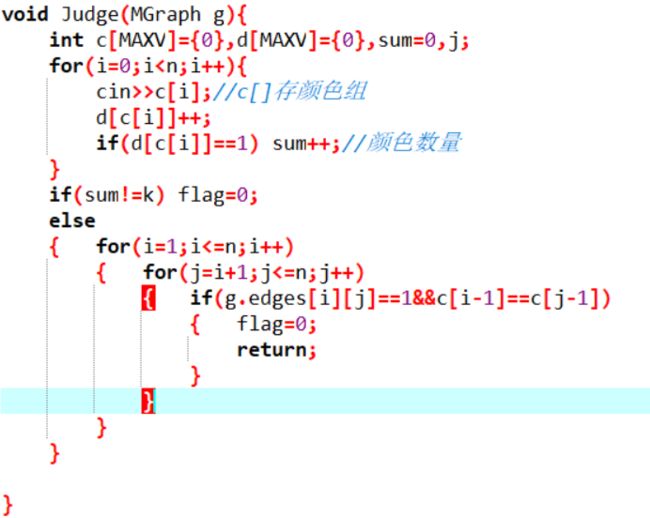
}Judge函数：
定义整型数组c[MAXV],d[MAXV]初始化为{0}，分别表示需要判断的颜色们，和每种颜色出现的次数
整型变量 sum统计颜色数量
for i=0 to i=n 共总顶点次
将颜色存入数组c[]中
d[c[i]]++统计该颜色出现的次数
如果 d[c[i]等于1] 即颜色c[i]第一次出现
颜色数sum++；
end for
如果（sum 不等于 题目要求颜色数量）
flag等于0
否则
for i=1 to i=n 遍历顶点i
for j=i+1 to j=n 遍历剩下的顶点，判断与顶点i的关系
如果（顶点i与顶点j有联系 且 i的颜色等于j的颜色）
flag=0；
return flag；
end if
end for（j）
end for（i）
end 否则
2.3 代码截图
- 1.主函数
- 2.建图函数
- 3.判断函数
2.4 PTA提交列表说明。
错误1：.：段错误
最大范围设置为500，应该为501
错误2：.：运行超时
将边数作为顶点数进行循环遍历
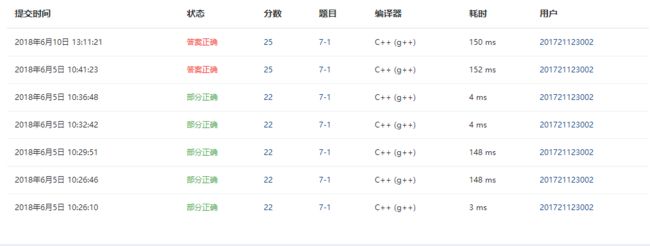
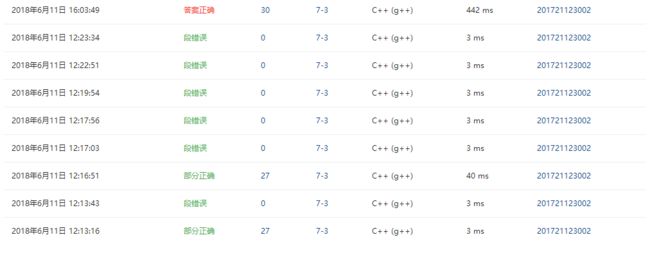
2.1 题目3：题目名称：7-2 排座位
2.2 设计思路
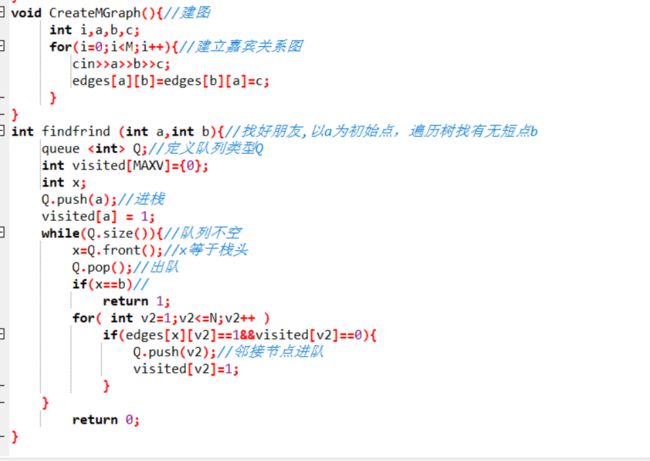
1.建图
以关系代表数为权值以矩阵储存建图
2.找朋友函数（部分）
int findfrind (int a,int b)找好朋友,以a为初始点，遍历树找有无端点b
深度遍历
如果 有遍历到顶点x 等于 b
return 1
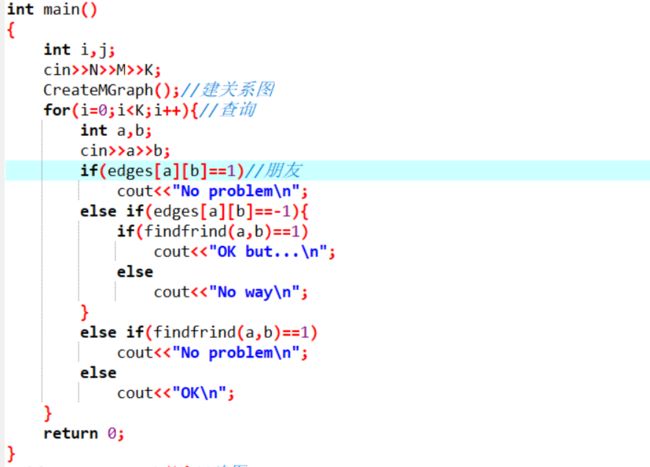
3.主函数（部分）
for i=0 to i=k共k次输入要判断的宾客
输入 a，b
如果 edges[a][b] 等于1
a和b是好朋友
如果 edges[a][b] 等于-1
如果 findfrind（a，b）等于 1
a和b是有共同好友的敌人
否则
a和b是纯敌人
如果 findfrind（a，b）等于 1
a和b通过共同好友成为好友
否则
a和b没有关系
2.3 代码截图
- 1.主函数
- 2.建图和查找查找函数
2.4 PTA提交列表说明。
一直处理不好朋友的朋友还是朋友的关系，所以一直卡在这个测试点
- 尝试1：a和b是好朋友，b和c，d,e等是好朋友，判断a与c,d,e的关系，如果不是敌对就变成好朋友
但是这样，a和c的朋友就没有进行关系建立 - 尝试2：a和b是好朋友，将b的好朋友且和a非敌对关系存入数组，然后再进行一个递归，将所有可以建立的关系建立，但是这样如果a和c先变成了好朋友，但其实之后的关系录入他们是敌人，但是之前的递归已经让c的部分朋友变成了a的朋友就产生了错误
- 尝试3：进行图的遍历，就是以上思路
3.截图本周题目集的PTA最后排名（3分）
本次题目集总分：310分
3.1 PTA排名
3.2 我的总分：200分
4. 阅读代码（必做，1分）
2833 奇怪的梦境
题目描述 Description
Aiden陷入了一个奇怪的梦境：他被困在一个小房子中，墙上有很多按钮，还有一个屏幕，上面显示了一些信息。屏幕上说，要将所有按钮都按下才能出去，而又给出了一些信息，说明了某个按钮只能在另一个按钮按下之后才能按下，而没有被提及的按钮则可以在任何时候按下。可是Aiden发现屏幕上所给信息似乎有矛盾，请你来帮忙判断。
输入描述 Input Description
第一行，两个数N，M，表示有编号为1...N这N个按钮，屏幕上有M条信息。
接下来的M行，每行两个数ai，bi，表示bi按钮要在ai之后按下。所给信息可能有重复，保证ai≠bi。
输出描述 Output Description
若按钮能全部按下，则输出“o(∩_∩)o”。
若不能，第一行输出“T_T”，第二行输出因信息有矛盾而无法确认按下顺序的按钮的个数。输出不包括引号。
#include
using namespace std ;
int n , m , cnt ;
int N = 10005 ;
int ind[N] ; //入度
int e[10001][10001] ;
stack s ;
void topsort(){
for ( int i = 1 ; i <= n ; i++ )
if (!ind[i]) s.push(i) ;
while (!s.empty()){
int point = s.top() ;
s.pop() ;
for ( int i = 1 ; i <= n ; i++ ){
if (e[point][i]){
ind[i]-- ;
if (!ind[i]) s.push(i) ;
}
}
}
for ( int i = 1 ; i <= n ; i++ )
if (ind[i]) cnt++ ;
}
int main(){
cin >> n >> m ;
int t1 , t2 ;
for ( int i = 1 ; i <= m ; i++ ){
scanf ("%d%d" , &t1 , &t2) ;
e[t1][t2] = 1 ;
ind[t2]++ ;
}
topsort() ;
if (cnt) printf("T_T\n%d" , cnt) ;
else cout << "o(∩_∩)o" ;
return 0 ;
}