pyTorch基础系列(一)—— 基本语法
目录
-1.torch.FloatTensor()
0. repeat
1. Varibale与Tensor的区别(0.4之后已经合并为一类了)
2. 大多数索引 都用LongTensor
3. import导入
4. 创建Tensors
5. 获取Tensor部分值
6. 产生随机数据
7. Tensor运算
8. torch.cat( [res,] x_1, x_2, [dimension] )
9. Tensor维度变型reshaping
10. Computation Graphs and Automatic Differentiation
11. 显示z中所有元素的和 s = z.sum()
12. Deep Learning Building Blocks: Affine maps, non-linearities and objectives
13. Softmax and Probabilitiessoftmax是x_i/sum(x)
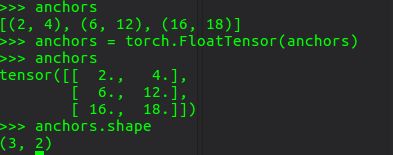
-1.torch.FloatTensor()元祖也能直接tensor
0. repeat
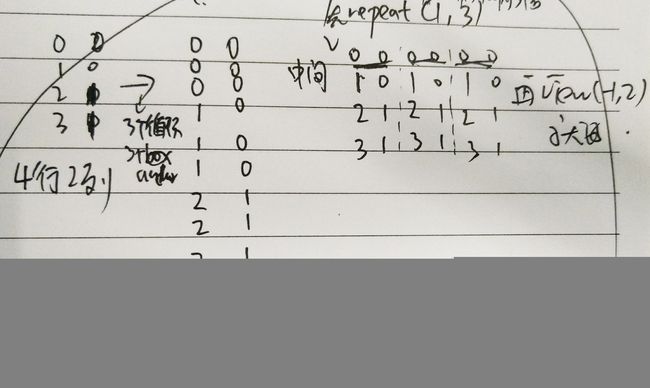
x.repeat(2,3) x的行数复制成原先2倍,列数复制成3倍,遍历循环for的替代。pytorch版本的yolov3中有用到!
grid = np.arange(grid_size)
a,b = np.meshgrid(grid, grid)
x_offset = torch.FloatTensor(a).view(-1,1)#13*13
y_offset = torch.FloatTensor(b).view(-1,1)
x_y_offset = torch.cat((x_offset, y_offset), 1).repeat(1,num_anchors).view(-1,2).unsqueeze(0)1. Varibale与Tensor的区别(0.4之后已经合并为一类了)
注意:rpn_score是 Variable 而rpn_label刚开始是tensor,因为anchor_target_layer和prosal_layer.py不需要反向传播,了解他们的输入输出这一点很简单,他们本身就是生成rpn_lable 等,做的事情是制定选出的规则,并没有对选出的东西进行计算,所以无需反向传播,所以里面的forward的input都是Tensor,输入的时候都需要 Variable.data, 运算完后的输出再用Variable( Tensor.long())转换回来。
Variable API 几乎和 Tensor API一致 (除了一些in-place方法,这些in-place方法会修改 required_grad=True的 input 的值)。多数情况下,将Tensor替换为Variable,代码一样会正常的工作。
在autograd中支持in-place operations是非常困难的。
所有的Variable都会记录用在他们身上的 in-place operations。如果pytorch检测到variable在一个Function中已经被保存用来backward,但是之后它又被in-place operations修改。当这种情况发生时,在backward的时候,pytorch就会报错。这种机制保证了,如果你用了in-place operations,但是在backward过程中没有报错,那么梯度的计算就是正确的。
2. 大多数索引 都用LongTensor
首先longTensor是64位的长整型。.long()
3. import导入
import torch#基本的torch函数
import torch.autograd as autograd#自动求导
import torch.nn as nn#神经网络类都在这个里面
import torch.nn.functional as F#几乎所有的激励函数
import torch.optim as optim#优化
4. 创建Tensors
#create 1D vector
V_data = [1., 2., 3.]
V = torch.Tensor(V_data)#我用的是pyCharm编辑器,输入torch给的提示没有Tensor函数,其实是有的
print(V)
1
2
3
[torch.FloatTensor of size 3]
#create 2D vector
M_data = [[1., 2., 3.], [4., 5., 6.]]
M = torch.Tensor(M_data)
print(M)
1 2 3
4 5 6
[torch.FloatTensor of size 2x3]
#create 3D vector
T_data = [[[1.,2.], [3.,4.]],
[[5.,6.], [7.,8.]]]
T = torch.Tensor(T_data)
print(T)
(0 ,.,.) =
1 2
3 4
(1 ,.,.) =
5 6
7 8
[torch.FloatTensor of size 2x2x2]
5. 获取Tensor部分值
#我就觉得这里比TensorFlow好用多了QAQ
print(V[0])
print(M[0])
print(T[0])
1.0
1
2
3
[torch.FloatTensor of size 3]
1 2
3 4
[torch.FloatTensor of size 2x2]
6. 产生随机数据
x = torch.randn((3,4,5))
print(x)
(0 ,.,.) =
1.4533 0.0593 0.2027 -1.0107 -0.3175
-0.1847 0.3021 0.0848 -1.2445 -0.5568
-0.2796 -0.5961 -0.3000 -0.2782 1.4920
1.4030 1.0875 -0.5814 -1.2006 0.2690
(1 ,.,.) =
-0.7093 -0.4939 0.7491 0.9133 0.4221
1.3949 2.5685 -0.4359 -0.7788 1.0251
1.6232 -1.2432 0.3403 -1.0551 1.3790
-1.5632 -0.9772 0.3963 -0.1890 0.0032
(2 ,.,.) =
-0.3360 -0.5571 -0.6641 -1.5845 -0.8766
-0.1809 -1.0035 1.7093 0.9176 1.6438
1.6955 0.6816 0.5978 -0.1379 -0.3877
1.0876 1.2371 -0.7378 -0.7647 0.0544
[torch.FloatTensor of size 3x4x5]
7. Tensor运算
x = torch.Tensor([1., 2., 3.])
y = torch.Tensor([4., 5., 6.])
z = x + y
print(z)
5
7
9
[torch.FloatTensor of size 3]
8. torch.cat( [res,] x_1, x_2, [dimension] )
x_1 = torch.randn(2, 5)
y_1 = torch.randn(3, 5)
z_1 =torch.cat([x_1, y_1])#没有最后一个参数,默认是0,则最终维度的第0维度为x_1与y_1第0维度的和,最终维度的其他维度不变.以下同理
print(z_1)
x_2 = torch.randn(2, 3)
y_2 = torch.randn(2, 5)
z_2 = torch.cat([x_2, y_2], 1)
print(z_2)
0.6372 0.7380 0.9324 0.0626 -0.3678
1.1819 2.1591 0.2445 0.0064 0.7760
-0.7765 -0.6797 0.1814 0.3948 1.7398
-0.2957 -0.6972 3.7052 -0.1943 0.4159
0.7385 -0.2365 1.4243 -0.0044 -0.7645
[torch.FloatTensor of size 5x5]
-0.0256 -0.6597 -0.1897 0.4361 0.1680 0.6513 -0.0433 -1.5741
-1.4514 0.0949 -0.7783 0.8568 -0.8722 0.0364 -0.0998 0.9265
[torch.FloatTensor of size 2x8]
9. Tensor维度变型reshaping
x = torch.randn(2, 3, 4)
print(x)
(0 ,.,.) =
0.6294 -0.3965 1.3737 1.6951
-0.5477 -1.5385 -0.0288 0.8104
-0.4208 -0.4469 0.0184 0.9507
(1 ,.,.) =
-0.2843 -0.0695 -0.1747 2.3774
1.1067 0.1980 -2.0712 -0.0670
-1.4900 0.0716 -0.7605 0.4611
[torch.FloatTensor of size 2x3x4]```
view转换维数
print(x.view(2,12))#将234 -> 2*12
Columns 0 to 9
0.6294 -0.3965 1.3737 1.6951 -0.5477 -1.5385 -0.0288 0.8104 -0.4208 -0.4469
-0.2843 -0.0695 -0.1747 2.3774 1.1067 0.1980 -2.0712 -0.0670 -1.4900 0.0716
Columns 10 to 11
0.0184 0.9507
-0.7605 0.4611
[torch.FloatTensor of size 2x12]```
print(x.view(2,-1))#-1的话,意味着最后的相乘为维数,这里为2*之后的成绩
#和上面的一样
Columns 0 to 9
0.6294 -0.3965 1.3737 1.6951 -0.5477 -1.5385 -0.0288 0.8104 -0.4208 -0.4469
-0.2843 -0.0695 -0.1747 2.3774 1.1067 0.1980 -2.0712 -0.0670 -1.4900 0.0716
Columns 10 to 11
0.0184 0.9507
-0.7605 0.4611
[torch.FloatTensor of size 2x12]
10. Computation Graphs and Automatic Differentiation
x = autograd.Variable(torch.Tensor([1., 2., 3]), requires_grad=True)
print(x)
print(x.data)#.data显示具体数据
#找不同
Variable containing:
1
2
3
[torch.FloatTensor of size 3]
1
2
3
[torch.FloatTensor of size 3]
y = autograd.Variable( torch.Tensor([4., 5., 6]), requires_grad=True )
z = x + y
print(z.data)
5
7
9
[torch.FloatTensor of size 3]
.creator是生成器
print(z.creator)
#因为是z = x + y 所以,z运算是add
11. 显示z中所有元素的和 s = z.sum()
s = z.sum()
print(s)
Variable containing:
21
[torch.FloatTensor of size 1]
s.backward()#反向传播
print(x.grad)#对x求导
Variable containing:
1
1
1
[torch.FloatTensor of size 3]
#答案解释
#x = [1,2,3]
#y = [4,5,6]
#z = x + y = [x0+y0, x1+y1, x2+y2]
#s = z.sum() = x0+y0+x1+y1+x2+y2
#x.grad 在s运算中对x求导 也就是当中的x0,x1,x2求导 为1,1,1
12. Deep Learning Building Blocks: Affine maps, non-linearities and objectives
Affine maps
也可以说是线性映射,即为f(x) = Ax + b
nn.Linear(inputSize,outputSize,bias=True)
输入(N, inputSize)
输出(N, outputSize)
lin = nn.Linear(5,3)
data = autograd.Variable(torch.randn(2, 5))
print(lin(data))
Variable containing:
-0.1838 -0.1833 -0.6425
0.2675 0.0263 0.0482
[torch.FloatTensor of size 2x3]
Non-Linearities
非线性,常用的函数有 tanh(x),σ(x),ReLU(x) 这些都是激励函数
在pytorch中大部分激励函数在torch.functional中
data = autograd.Variable( torch.randn(2, 2) )
print(data)
print (F.relu(data))#relu函数是小于零是0,大于零就是它本身
Variable containing:
-2.0620 1.4252
0.5694 0.2251
[torch.FloatTensor of size 2x2]
Variable containing:
0.0000 1.4252
0.5694 0.2251
[torch.FloatTensor of size 2x2]
13. Softmax and Probabilities
softmax是x_i/sum(x)
data = autograd.Variable( torch.randn(5) )
print(data)
print(F.softmax(data))
print(F.softmax(data).sum())
print(F.log_softmax(data))
Variable containing:
0.6861
0.1695
-0.4775
-2.0097
0.7039
[torch.FloatTensor of size 5]
Variable containing:
0.3340
0.1992
0.1043
0.0225
0.3400
[torch.FloatTensor of size 5]
Variable containing:
1
[torch.FloatTensor of size 1]
Variable containing:
-1.0967
-1.6133
-2.2604
-3.7925
-1.0789
[torch.FloatTensor of size 5]
作者:zenRRan
链接:https://www.jianshu.com/p/7593aadab004
來源:简书
简书著作权归作者所有,任何形式的转载都请联系作者获得授权并注明出处。