北京PM2.5情况分析(2010-2014)
利用网上搜集到的CSV数据,对北京市2010年至2014年的PM2.5情况进行分析。
数据获取
数据来源于 UC Irvine Machine Learning Repository网站中的Beijing PM2.5 Data Data Set,数据文件类型为CSV。
数据清洗预览:
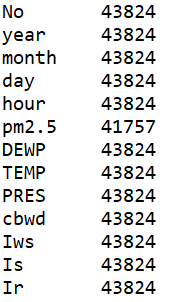
数据共43824条,13个维度,其中部分字段代表含义如下
TEMP:温度
PRES:大气压力
cbwd:风向
Iws:风速
Is:是否下雪
Ir:是否下雨
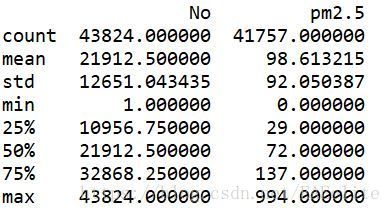
从数据中,可以发现pm2.5数据列中存在缺失值,2010-2014年的北京pm2.5的均值为98.6,中位数为92.0,区间为[0,994].
pm2.5数据反映的是某一日某一时刻的pm2.5值,观察缺失值,发现有的是某一日的值都缺失,有的是某一日的某几个时刻的值缺失。打算以天为单位统计pm2.5的值,所以若某一日中出现了缺失值,则删除该日的所有时刻的pm2.5值,即处理缺失值的方法为删除记录。
数据清洗之后,再经过数据集成和数据变换,最终可用数据数量如下所示,单位为:天数
数据分析可视化:
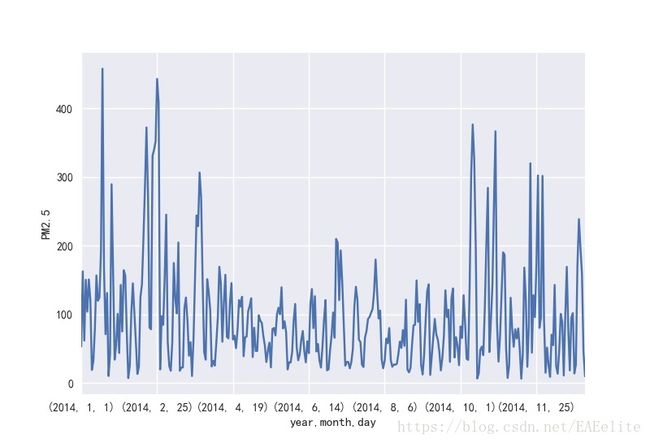
以天为单位,统计出每年的pm2.5值的变化情况,以2014年为例,如下图所示。
可以看出,4月-9月的pm2.5值要低于于10月-3月的pm2.5值,4月至9月的空气条件更好。
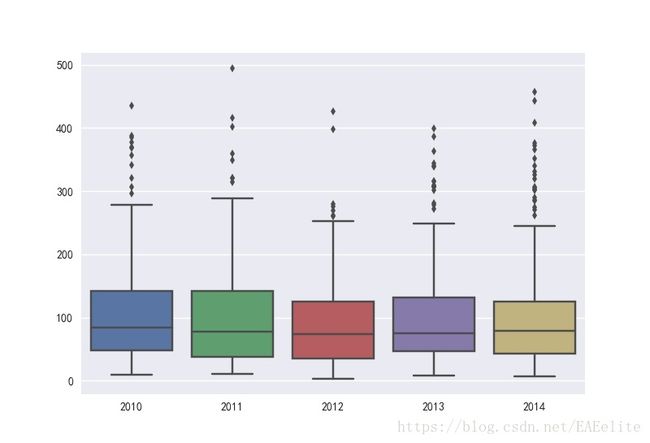
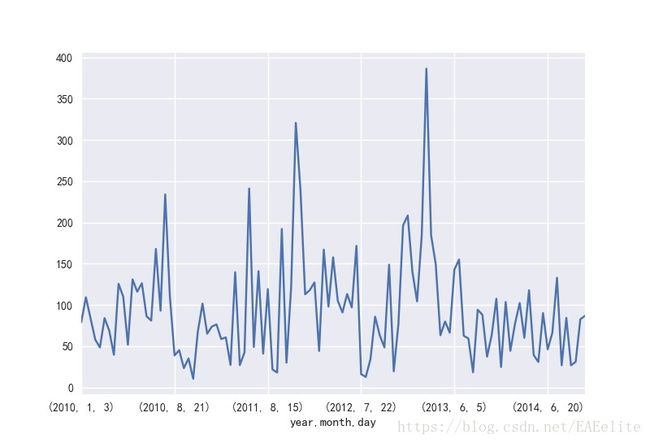
接下来,将2010-2014年的pm2.5值统计情况放在同一张图上,直观的看待这几年的变化。
从图中可以看出,近几年的pm2.5值稍有下降,箱式图上各分位数的值都是有所降低的。同时,每年也都存在异常值,且异常值的大小和数量没有明显的减少。为了更明显的发现统计规律,按照国家PM2.5检测网的空气质量的标准,根据24小时平均值标准值的分布来划分每天的空气质量等级,划分依据如下:
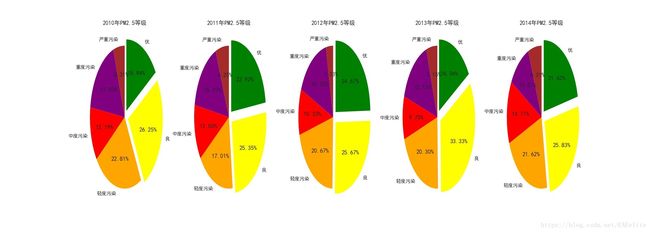
将数据按照空气质量等级和颜色划分后,绘制饼状图。
可以看出,2010年至1014年,北京市pm2.5等级为优良的天数占比分别为42.19%、48.27%、50.34%、49.69%和47.45%。相比于2010年,后四年的优良天数明显增多,pm2.5空气质量得到明显改善。
下面分析pm2.5空气质量等级改善的原因:
(1)降水
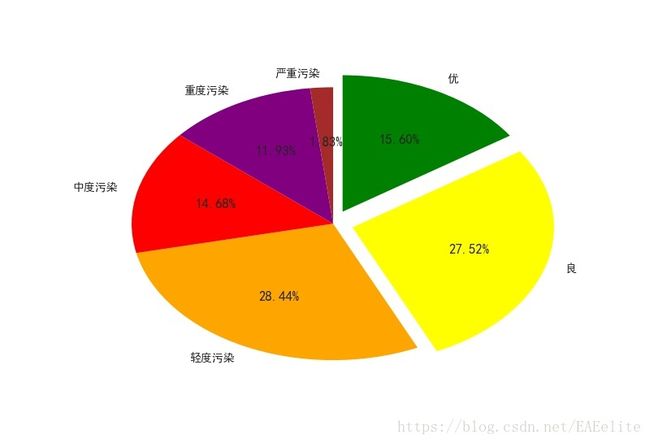
根据数据表中的降雨和降雪情况,找到降水超过6小时的日期,将这些日期对应的PM2.5值绘制图形,如下所示。
可以看出,除了少数几天外,绝大部分的pm2.5值都能控制在150以下,低于中度污染级别,优良级别的天数占比43.12%。
结论,pm2.5值不会因为降水而下降,空气质量不会因为降水而得到缓解
(2)刮风
根据数据提供的风向和风速情况,找到一天之内累计风速大于48m/s(相当于持续刮4级风累计6小时)的日期对应的pm2.5值,绘图如下所示
可以看出,这些日期中pm2.5值属于优良等级的占比为64.03%,比之前的优良率提高了很多。
结论
实际测量数值显示,降水和pm2.5数值没有因果性,降水本身并不能带动空气中的颗粒物沉降,颗粒物的浓度不会明显降低,降水不会对pm2.5数值产生显著影响。刮风可以显著降低pm2.5值,空气中颗粒物是被吹跑了而非沉降,浓度降低,pm2.5值明显下降。
看来提高空气质量,降低pm2.5的有效措施不是盼下雨而是等风来!
利用时间序列ARMA模型分析并预测pm2.5值
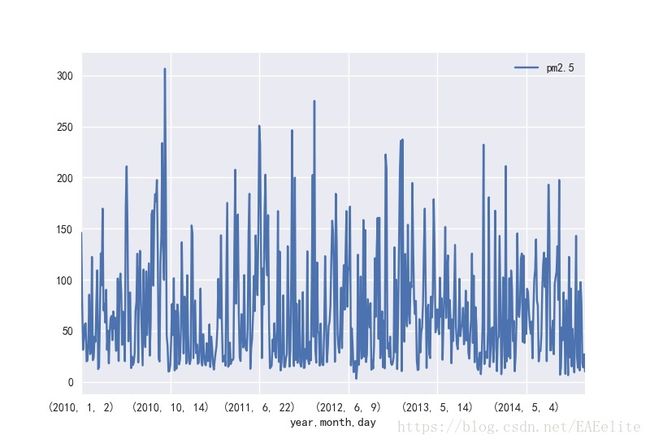
还是以天为单位分析这五年之内的pm2.5值,并绘制曲线
ARIMA 模型对时间序列的要求是平稳型,观察图标能看出其没有固定的上升或下降的趋势,粗略判断是平稳序列。不进行差分操作,同时使用ADF单位根平稳型检验,对序列进行平稳性检验。
from statsmodels.tsa.stattools import adfuller as ADF
ADF(test)
#返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore得到结果如下:
(-18.23039005254537, 2.3680392326349674e-30, 2, 1568,
{'1%': -3.434527319939446, '10%': -2.56775226495796, '5%': -2.863385036059078}, 17309.834345756433)
- 1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较,ADF Test result同时小于1%、5%、10%即说明非常好地拒绝该假设.本数据中,adf结果为-18.23, 小于三个level的统计值。
- P-value是否非常接近0.本数据中,P-value 为 2.36e-30,接近0.
ADF检验的原假设是存在单位根,只要这个统计值是小于1%水平下的数字就可以极显著的拒绝原假设,认为数据平稳。
选择合适的ARMA模型
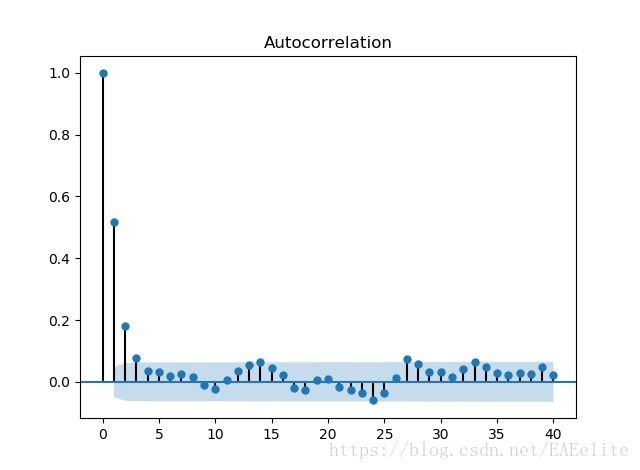
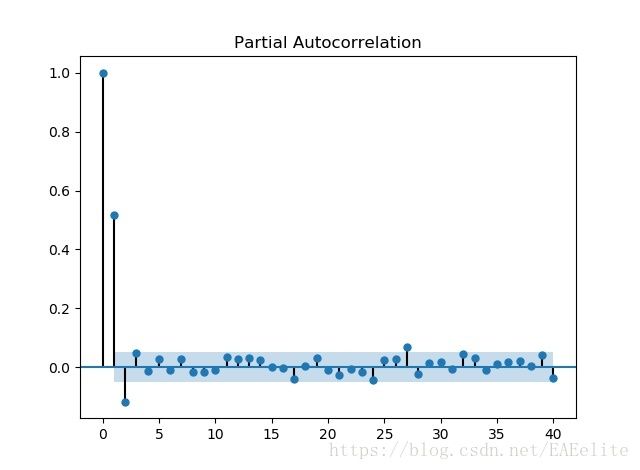
关注序列的自相关图(ACF)和偏自相关图(PACF)
为了避免计算量过大,这里只显示前40阶数据,根据ARMA模型的特征系数选取方法,
可以从ACF和PACF中看出,两图各有3阶在置信区间以外,故选择模型为ARMA(0,3),ARMA(3,0),ARMA(3,3)。
采用ARMA模型的AIC法则,计算三个模型的aic,bic,hqic。
(17593.54679692005, 17620.34413511133, 17603.50667290371)
(17594.582065024613, 17621.37940321589, 17604.541941008272)
(17596.96193511383, 17639.837676219875, 17612.897736687686)
取值最小的模型ARMA(0,3),避免出现过度拟合的情况。
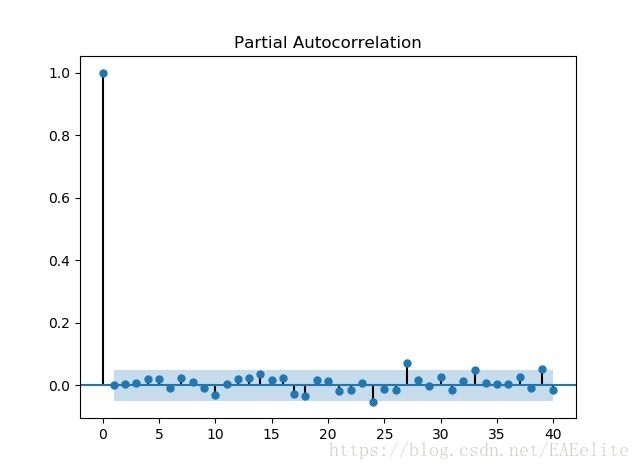
观察残差
画出ARMA(0,3)模型的ACF和PACF图
可以看出残差属于一阶模型,然后进行德宾-沃森(Durbin-Watson)检验,检验结果是1.9981680279811966,说明残差序列不存在自相关性。
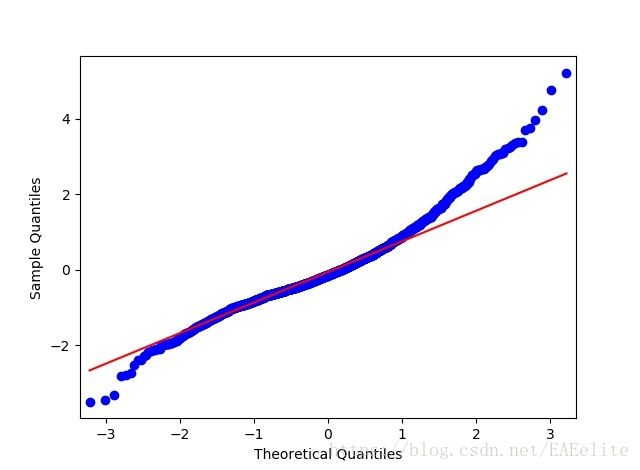
使用QQ图检查残差序列是否服从正态分布,它直观验证一组数据是否来自某个分布,或者验证某两组数据是否来自同一(族)分布。
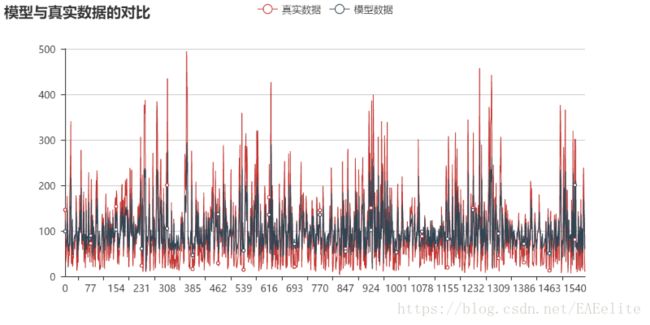
观察模型的预测情况
图中是真实数据和模型拟合数据的可视化,其中红色的折线是原始数据的可视化,黑色的折线是模型对红色数据预测的结果的可视化。从图中可以看出,模型基本上模拟出了原始序列的趋势,