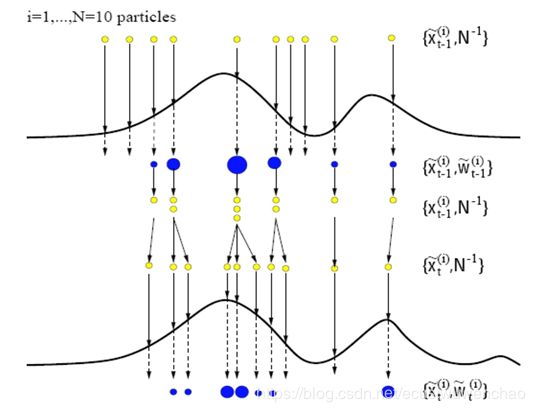
粒子滤波详解
粒子滤波 Particle Filter
- 1.1 贝叶斯滤波(Bayes filters)
- 1.1.1 马尔科夫假设
- 1.1.2 贝叶斯滤波算法推导
- 1.2 蒙特卡洛方法 (Monte Carlo method)
- 1.2.1 蒙特卡洛方法
- 1.2.2 蒙特卡洛思想在贝叶斯滤波中的应用
- 1.3 重要性采样 (Importance Sampling)
- 1.4 序贯重要性采样 (Sequential Importance Sampling, SIS)
- 1.5 重采样 (Resampling)
- 1.6 粒子滤波算法完整流程
声明:本文仅作为个人复习与分享,里面很多内容是对其他博文的整理,在文章中均有注明。本人小白一枚,文章中如有错误,希望各位提醒!
粒子滤波通过非参数化的蒙特卡洛(Monte Carlo)模拟方法来实现递推贝叶斯滤波,适用于任何能用状态空间模型描述的非线性系统,精度可以逼近最优估计。粒子滤波器具有简单、易于实现等特点,它为分析非线性动态系统提供了一种有效的解决方法,从而引起目标跟踪、信号处理以及自动控制等领域的广泛关注。 本文从基础的贝叶斯滤波开始介绍,再引出蒙特卡罗采样,重要性采样,粒子滤波。
1.1 贝叶斯滤波(Bayes filters)
贝叶斯滤波将状态估计视为一个概率推理过程,即将目标状态的估计问题转换为利用贝叶斯公式求解后验概率密度或滤波概率密度,进而获得目标状态的最优估计。关于贝叶斯滤波的讲解,有一篇博文个人觉得写得很好,我这里借鉴了这篇文章的思路,具体博文地址见链接https://www.cnblogs.com/ycwang16/p/5995702.html
1.1.1 马尔科夫假设
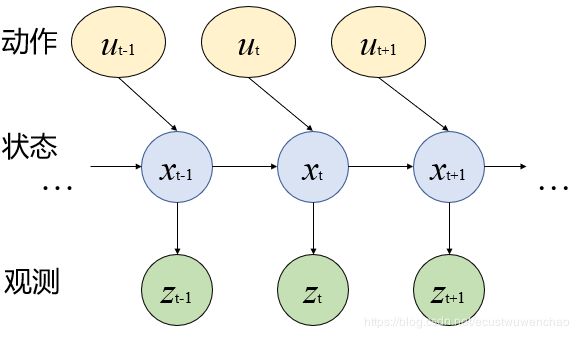
根据马尔科夫性假设,t时刻的状态由t−1时刻的状态和t时刻的动作决定。t时刻的观测仅同t时刻的状态相关,如图1所示
1.1.2 贝叶斯滤波算法推导
给定t时刻以及之前的所有观测z和输入u,我们的目标是求得当前状态量x的概率分布(belief),即
b e l ( x t ) = p ( x t ∣ z 1 : t , u 1 : t ) bel(x_{t})=p(x_{t}|z_{1:t},u_{1:t}) bel(xt)=p(xt∣z1:t,u1:t)
在实际使用中,一般将求解过程分为两步,首先求解在t时刻观测前的先验分布,即
b e l ‾ ( x t ) = p ( x t ∣ z 1 : t − 1 , u 1 : t ) \overline {bel}(x_{t})=p(x_{t}|z_{1:t-1},u_{1:t}) bel(xt)=p(xt∣z1:t−1,u1:t)
然后再根据t时刻的观测通过贝叶斯公式更新先验分布,以得到后验分布,即
b e l ( x t ) = η p ( z t ∣ x t , z 1 : t − 1 , u 1 : t ) b e l ‾ ( x t ) bel(x_{t})=\eta p(z_{t}|x_{t},z_{1:t-1},u_{1:t})\overline {bel}(x_{t}) bel(xt)=ηp(zt∣xt,z1:t−1,u1:t)bel(xt)
其中η是归一化系数。
进一步,t时刻的先验分布可以根据全概率公式用t-1时刻的后延分布表示,即
b e l ‾ ( x t ) = p ( x t ∣ z 1 : t − 1 , u 1 : t ) = ∫ p ( x t , x t − 1 ∣ z 1 : t − 1 , u 1 : t ) d x t − 1 = ∫ p ( x t ∣ x t − 1 , z 1 : t − 1 , u 1 : t ) p ( x t − 1 ∣ z 1 : t − 1 , u 1 : t ) d x t − 1 \overline {bel}(x_{t})=p(x_{t}|z_{1:t-1},u_{1:t}) =\int p(x_{t},x_{t-1}|z_{1:t-1},u_{1:t})dx_{t-1}\\ =\int p(x_{t}|x_{t-1},z_{1:t-1},u_{1:t})p(x_{t-1}|z_{1:t-1},u_{1:t})dx_{t-1} bel(xt)=p(xt∣z1:t−1,u1:t)=∫p(xt,xt−1∣z1:t−1,u1:t)dxt−1=∫p(xt∣xt−1,z1:t−1,u1:t)p(xt−1∣z1:t−1,u1:t)dxt−1
根据马尔科夫性假设,t-1时刻的状态与t时刻的输入无关,那么
p ( x t − 1 ∣ z 1 : t − 1 , u 1 : t ) = p ( x t − 1 ∣ z 1 : t − 1 , u 1 : t − 1 ) = b e l ( x t − 1 ) p(x_{t-1}|z_{1:t-1},u_{1:t})=p(x_{t-1}|z_{1:t-1},u_{1:t-1})=bel(x_{t-1}) p(xt−1∣z1:t−1,u1:t)=p(xt−1∣z1:t−1,u1:t−1)=bel(xt−1)
b e l ‾ ( x t ) = ∫ p ( x t ∣ x t − 1 , z 1 : t − 1 , u 1 : t ) b e l ( x t − 1 ) d x t − 1 \overline {bel}(x_{t})=\int p(x_{t}|x_{t-1},z_{1:t-1},u_{1:t})bel(x_{t-1})dx_{t-1} bel(xt)=∫p(xt∣xt−1,z1:t−1,u1:t)bel(xt−1)dxt−1
进一步根据马尔科夫性假设,即t时刻的状态只和t时刻的输入以及t-1时刻的状态有关,t时刻的观测只和t时刻的状态有关,那么
p ( x t ∣ x t − 1 , z 1 : t − 1 , u 1 : t ) = p ( x t ∣ x t − 1 , u t ) p(x_{t}|x_{t-1},z_{1:t-1},u_{1:t})=p(x_{t}|x_{t-1},u_{t}) p(xt∣xt−1,z1:t−1,u1:t)=p(xt∣xt−1,ut)
p ( z t ∣ x t , z 1 : t − 1 , u 1 : t ) = p ( z t ∣ x t ) p(z_{t}|x_{t},z_{1:t-1},u_{1:t})=p(z_{t}|x_{t}) p(zt∣xt,z1:t−1,u1:t)=p(zt∣xt)
最终可得贝叶斯滤波器的更新方程
b e l ‾ ( x t ) = ∫ p ( x t ∣ x t − 1 , u t ) b e l ( x t − 1 ) d x t − 1 \overline {bel}(x_{t})=\int p(x_{t}|x_{t-1},u_{t})bel(x_{t-1})dx_{t-1} bel(xt)=∫p(xt∣xt−1,ut)bel(xt−1)dxt−1
b e l ( x t ) = η p ( z t ∣ x t ) b e l ‾ ( x t ) bel(x_{t})=\eta p(z_{t}|x_{t})\overline {bel}(x_{t}) bel(xt)=ηp(zt∣xt)bel(xt)
一个完整的贝叶斯滤波器就是随着时间推移不断执行以上两步来完成状态量的估计。
注:这里的推导过程借鉴了博文https://www.cnblogs.com/aipiano/p/9060054.html
1.2 蒙特卡洛方法 (Monte Carlo method)
1.2.1 蒙特卡洛方法
简单来说,蒙特卡罗方法就是一种计算方法。原理是通过大量随机样本,去了解一个系统,进而得到所要计算的值。它非常强大和灵活,又相当简单易懂,很容易实现。对于许多问题来说,它往往是最简单的计算方法,有时甚至是唯一可行的方法。比如上一小节介绍了贝叶斯滤波的推导过程中需要用到积分,这对于一般的非线性,非高斯系统,很难得到后验概率的解析解。为了解决这个问题,通常采用蒙特卡洛采样。
假设我们能从一个目标概率分布p(x)中采样到一系列的样本(粒子),(至于怎么生成服从p(x)分布的样本,这个问题先放一放),那么就能利用这些样本去估计这个分布的某些函数的期望值。譬如:
E [ f ( x ) ] = ∫ f ( x ) p ( x ) d x E[f(x)]=\int f(x)p(x)dx E[f(x)]=∫f(x)p(x)dx
V a r [ f ( x ) ] = ∫ ( f ( x ) − E [ f ( x ) ] ) 2 p ( x ) d x Var[f(x)]=\int(f(x)-E[f(x)])^{2} p(x)dx Var[f(x)]=∫(f(x)−E[f(x)])2p(x)dx
上面的式子其实都是计算期望的问题,只是被积分的函数不同。蒙特卡洛采样的思想就是用平均值来代替积分,求期望:
E [ f ( x ) ] ≈ 1 N ∑ i = 1 N f ( x i ) E[f(x)]\approx \frac{1}{N}\sum_{i=1}^{N}f(x_{i}) E[f(x)]≈N1i=1∑Nf(xi)
这可以从伯努利大数定律的角度去理解它。我们用这种思想去指定不同的f(x)以便估计不同问题。
1.2.2 蒙特卡洛思想在贝叶斯滤波中的应用
首先,假设我们可以从后验概率 p ( x n ∣ Y n ) p(x_{n}|Y_{n}) p(xn∣Yn)中采集到N个独立样本 { x n ( 1 ) , x n ( 2 ) , … , x n ( N ) } \{x_{n}^{(1)}, x_{n}^{(2)},\ldots, x_{n}^{(N)}\} {xn(1),xn(2),…,xn(N)},那么后验概率的计算可以表示为:
p ~ ( x n ∣ Y n ) ≈ 1 N Σ i = 1 N δ ( x n − x n ( i ) ) \tilde{p}(x_{n}|Y_{n}) \approx \frac{1}{N}\Sigma_{i=1}^{N}\delta(x_{n} - x_{n}^{(i)}) p~(xn∣Yn)≈N1Σi=1Nδ(xn−xn(i))
其中, δ ( x n − x n ( i ) ) \delta(x_{n} - x_{n}^{(i)}) δ(xn−xn(i))为单位冲激函数(狄拉克函数)。
估计出了后验概率,要做滤波就要知道当前状态的期望值:
E ( f ( x n ) ≈ ∫ f ( x n ) p ~ ( x n ∣ Y n ) d x n = 1 N Σ i = 1 N f ( x n ( i ) ) E(f(x_{n}) \approx \int f(x_{n}) \tilde{p}(x_{n}|Y_{n})\,dx_{n} = \frac{1}{N}\Sigma_{i=1}^{N}f(x_{n}^{(i)}) E(f(xn)≈∫f(xn)p~(xn∣Yn)dxn=N1Σi=1Nf(xn(i))
可以看出,只要我们使用采样粒子的状态值的平均就能得到期望值,也就是滤波后的值,这里的 f ( x ) f(x) f(x)就是每个粒子的状态函数。这就是粒子滤波名字的由来了,只要从后验概率中采样很多粒子,用它们的状态求平均就得到了滤波结果。
这里产生了一个问题:没有后验概率却要从后验概率中采集样本去逼近后验概率和状态期望,于是引出了重要性采样算法。
1.3 重要性采样 (Importance Sampling)
当我们无法从一个未知的分布中采样的时候,重要性采样引入了一个容易采样的重要性概率密度函数 q ( x n ∣ Y n ) q(x_{n}|Y_{n}) q(xn∣Yn),重要性采样的思想就是从这个重要性概率密度函数中采样粒子,然后使用采样的结果去加权逼近我们的后验概率密度函数 p ( x n ∣ Y n ) p(x_{n}|Y_{n}) p(xn∣Yn)
首先引入一个支撑粒子集{ ( x n ( i ) , w n ( i ) ) , i = 1 , 2 , . . . , N {(x_{n}^{(i)},w_{n}^{(i)}),i=1,2,...,N} (xn(i),wn(i)),i=1,2,...,N} ,其中是从重要性概率密度函数中采样的粒子,表示在n时刻第i个粒子的状态, w n ( i ) w_{n}^{(i)} wn(i)是其的权值。
那么后验概率密度函数可以表示为:
p ( x n ∣ Y n ) = ∑ i = 1 N w n ( i ) δ ( x n − x n i ) p(x_{n}|Y_{n})=\sum_{i=1}^{N}w_{n}^{(i)}\delta(x_{n}-x_{n}^{i}) p(xn∣Yn)=i=1∑Nwn(i)δ(xn−xni)
其中, w n ( i ) ∝ p ( x n ∣ Y n ) q ( x n ∣ Y n ) w_{n}^{(i)}\propto \frac{p(x_{n}|Y_{n})}{q(x_{n}|Y_{n})} wn(i)∝q(xn∣Yn)p(xn∣Yn)
根据蒙特卡洛思想,当采样粒子数目非常大的时候,就可以逼近概率密度函数,那么 f ( x n ) f(x_{n}) f(xn)的期望为:
E ( f ( x n ) = 1 N ∑ i = 1 N f ( x n ( i ) ) p ( x n ∣ Y n ) q ( x n ∣ Y n ) = 1 N ∑ i = 1 N f ( x n ( i ) ) w n ( i ) E(f(x_{n})= \frac{1}{N}\sum_{i=1}^{N}f(x_{n}^{(i)})\frac{p(x_{n}|Y_{n})}{q(x_{n}|Y_{n})}= \frac{1}{N}\sum_{i=1}^{N}f(x_{n}^{(i)})w_{n}^{(i)} E(f(xn)=N1i=1∑Nf(xn(i))q(xn∣Yn)p(xn∣Yn)=N1i=1∑Nf(xn(i))wn(i)
还有另外一种思路,直接求解期望:
E ( f ( x n ) = ∫ f ( x n ) p ( x n ∣ Y n ) q ( x n ∣ Y n ) q ( x n ∣ Y n ) d x = ∫ f ( x n ) p ( Y n ∣ x n ) p ( x n ) p ( Y n ) q ( x n ∣ Y n ) q ( x n ∣ Y n ) d x = ∫ f ( x n ) w n p ( Y n ) q ( x n ∣ Y n ) d x E(f(x_{n})= \int f(x_{n})\frac{p(x_{n}|Y_{n})}{q(x_{n}|Y_{n})}{q(x_{n}|Y_{n})}dx =\int f(x_{n})\frac{p(Y_{n}|x_{n})p(x_{n})}{p(Y_{n})q(x_{n}|Y_{n})}{q(x_{n}|Y_{n})}dx\\ =\int f(x_{n})\frac{w_{n}}{p(Y_{n})}{q(x_{n}|Y_{n})}dx E(f(xn)=∫f(xn)q(xn∣Yn)p(xn∣Yn)q(xn∣Yn)dx=∫f(xn)p(Yn)q(xn∣Yn)p(Yn∣xn)p(xn)q(xn∣Yn)dx=∫f(xn)p(Yn)wnq(xn∣Yn)dx
其中, w n ( x n ) w_{n}(x_{n}) wn(xn)表示时刻n粒子 x n x_{n} xn的权重,和上面的 w n ( i ) w_{n}^{(i)} wn(i)一个意思,只是表示形式不同,且:
w n = p ( Y n ∣ x n ) p ( x n ) q ( x n ∣ Y n ) ∝ p ( x n ∣ Y n ) q ( x n ∣ Y n ) w_{n}=\frac{p(Y_{n}|x_{n})p(x_{n})}{q(x_{n}|Y_{n})} \ \propto \frac{p(x_{n}|Y_{n})}{q(x_{n}|Y_{n})} wn=q(xn∣Yn)p(Yn∣xn)p(xn) ∝q(xn∣Yn)p(xn∣Yn)
又因为 p ( Y n ) = ∫ p ( Y n ∣ x n ) p ( x n ) d x n p(Y_{n})=\int p(Y_{n}|x_{n})p(x_{n})dx_{n} p(Yn)=∫p(Yn∣xn)p(xn)dxn
因此可以进行下一步推导:
E ( f ( x n ) ) = 1 p ( Y n ) ∫ f ( x n ) w n ( x n ) q ( x n ∣ Y n ) d x n = ∫ f ( x n ) w n ( x n ) q ( x n ∣ Y n ) d x n ∫ p ( Y n ∣ x n ) p ( x n ) d x n = ∫ f ( x n ) w n ( x n ) q ( x n ∣ Y n ) d x n ∫ w ( x n ) q ( x n ) d x n = E q ( x n ∣ Y n ) [ w n ( x n ) f ( x n ) ] E q ( x n ∣ Y n ) [ w n ( x n ) ] E(f(x_{n}))=\frac{1}{p(Y_{n})}\int f(x_{n})w_{n}(x_{n})q(x_{n}|Y_{n})dx_{n} =\frac{\int f(x_{n})w_{n}(x_{n})q(x_{n}|Y_{n})dx_{n}}{\int p(Y_{n}|x_{n})p(x_{n})dx_{n}} \\=\frac{\int f(x_{n})w_{n}(x_{n})q(x_{n}|Y_{n})dx_{n}}{\int w(x_{n})q(x_{n})dx_{n}} =\frac{E_{q(x_{n}|Y_{n})}[w_{n}(x_{n})f(x_{n})]}{E_{q(x_{n}|Y_{n})}[w_{n}(x_{n})]} E(f(xn))=p(Yn)1∫f(xn)wn(xn)q(xn∣Yn)dxn=∫p(Yn∣xn)p(xn)dxn∫f(xn)wn(xn)q(xn∣Yn)dxn=∫w(xn)q(xn)dxn∫f(xn)wn(xn)q(xn∣Yn)dxn=Eq(xn∣Yn)[wn(xn)]Eq(xn∣Yn)[wn(xn)f(xn)]
通过这一系列推导我们可以看出最后的期望已经转为完全与 q ( x n ∣ Y n ) q(x_{n}|Y_{n}) q(xn∣Yn)有关的期望求解了,这也是这个算法让我叹服的地方。这样我们就可以使用蒙特卡洛方法求解了,所以我们只要N个粒子的平均求其期望即可,上面的式子近似为:
E ( f ( x n ) ) ≈ 1 N ∑ i = 1 N w n ( x n ( i ) ) f ( x n ( i ) ) 1 N ∑ i = 1 N w n ( x n ( i ) ) = 1 N ∑ i = 1 N f ( x n ( i ) ) w ˉ n ( x n ( i ) ) E(f(x_{n}))\approx \frac{\frac{1}{N}\sum_{i=1}^{N}w_{n}(x_{n}^{(i)})f(x_{n}^{(i)})}{\frac{1}{N}\sum_{i=1}^{N}w_{n}(x_{n}^{(i)})}=\frac{1}{N}\sum_{i=1}^{N} f(x_{n}^{(i)})\bar w_{n}(x_{n}^{(i)}) E(f(xn))≈N1∑i=1Nwn(xn(i))N1∑i=1Nwn(xn(i))f(xn(i))=N1i=1∑Nf(xn(i))wˉn(xn(i))
这里的 w ˉ n ( x n ( i ) ) = w n ( x n ( i ) ) ∑ i = 1 N w n ( x n ( i ) ) \bar w_{n}(x_{n}^{(i)})=\frac{w_{n}(x_{n}^{(i)})}{\sum_{i=1}^{N} w_{n}(x_{n}^{(i)})} wˉn(xn(i))=∑i=1Nwn(xn(i))wn(xn(i))为归一化的权值,这个结果其实与上面的结果完全相同,只是一个权值是人为给出来的,一个是推导得出的。
这里的不是所有粒子的平均值而是所有粒子的加权和,每个粒子都有一个权重,可以理解为对当前粒子的信任程度,这样就解决了采样的问题,但此方法对于每次产生新的观测数据都要全部重新计算整个状态序列的重要性权值,计算量相当大,下面就引入序贯重要性采样来解决这种问题。
本节的公式推导引用了文章的推导方式作者:桑燊(https://zhuanlan.zhihu.com/p/26783371)
1.4 序贯重要性采样 (Sequential Importance Sampling, SIS)
对于上节所述的问题,本节将统计学中的序贯分析方法应用到蒙特卡洛方法中,进而实现后验概率密度的递推估计。
假设重要性概率密度函数为 q ( x 0 : n ∣ y 1 : n ) q(x_{0:n}|y_{1:n}) q(x0:n∣y1:n)(注意这里是 x 0 : n x_{0:n} x0:n与上一节有所区别),假设该密度函数可以分解如下:
q ( x 0 : n ∣ y 1 : n ) = q ( x 0 : n − 1 ∣ y 1 : n − 1 ) q ( x n ∣ x 0 : n − 1 , y 1 : n ) q(x_{0:n}|y_{1:n})= q(x_{0:n-1}|y_{1:n-1})q(x_{n}|x_{0:n-1},y_{1:n}) q(x0:n∣y1:n)=q(x0:n−1∣y1:n−1)q(xn∣x0:n−1,y1:n)
下面 X n 为 x 0 : n − 1 , Y n = y 1 : n X_{n}为x_{0:n-1},Y_{n}=y_{1:n} Xn为x0:n−1,Yn=y1:n
声明如下:
(1) 系统是一个一阶马尔科夫过程,即: p ( X n ) = p ( x 0 : n ) = p ( x 0 ) ∏ i = 1 n p ( x i ∣ x i − 1 ) p(X_{n}) = p(x_{0:n}) = p(x_{0})\prod_{i=1}^{n}p(x_{i}|x_{i-1}) p(Xn)=p(x0:n)=p(x0)∏i=1np(xi∣xi−1)
(2) 各次观测之间相互独立,即: p ( y 1 : n ∣ x 1 : n ) = ∏ i = 1 n p ( y i ∣ x i ) p(y_{1:n}|x_{1:n}) = \prod_{i=1}^{n}p(y_{i}|x_{i}) p(y1:n∣x1:n)=∏i=1np(yi∣xi)
那么后验概率密度函数的递推如下:
p ( X n ∣ Y n ) = p ( Y n ∣ X n ) p ( X n ) p ( Y n ) = p ( y n , Y n − 1 ∣ X n ) p ( X n ) p ( y n ∣ Y n − 1 ) p ( Y n − 1 ) = p ( y n ∣ X n , Y n − 1 ) p ( Y n − 1 ∣ X n ) p ( X n ) p ( y n ∣ Y n − 1 ) p ( Y n − 1 ) = p ( y n ∣ X n , Y n − 1 ) p ( X n ∣ Y n − 1 ) p ( y n ∣ Y n − 1 ) = p ( y n ∣ X n , Y n − 1 ) p ( x n ∣ X n − 1 , Y n − 1 ) p ( X n − 1 ∣ Y n − 1 ) p ( y n ∣ Y n − 1 ) = p ( y n ∣ x n ) p ( x n ∣ x n − 1 ) p ( X n − 1 ∣ Y n − 1 ) p ( y n ∣ Y n − 1 ) ∝ p ( y n ∣ x n ) p ( x n ∣ x n − 1 ) p ( X n − 1 ∣ Y n − 1 ) p(X_{n}|Y_{n}) = \frac {p(Y_{n}|X_{n})p(X_{n})}{p(Y_{n})}=\frac{p(y_{n},Y_{n-1}|X_{n})p(X_{n})}{p(y_{n}|Y_{n-1})p(Y_{n-1})} \\=\frac{p(y_{n}|X_{n},Y_{n-1})p(Y_{n-1}|X_{n})p(X_{n})}{p(y_{n}|Y_{n-1})p(Y_{n-1})} \\ = \frac{p(y_{n}|X_{n},Y_{n-1})p(X_{n}|Y_{n-1})}{p(y_{n}|Y_{n-1})}\\ =\frac{p(y_{n}|X_{n},Y_{n-1})p(x_{n}|X_{n-1},Y_{n-1})p(X_{n-1}|Y_{n-1})}{p(y_{n}|Y_{n-1})}\\ = \frac{p(y_{n}|x_{n})p(x_{n}|x_{n-1})p(X_{n-1}|Y_{n-1})}{p(y_{n}|Y_{n-1})} \\ \propto p(y_{n}|x_{n})p(x_{n}|x_{n-1})p(X_{n-1}|Y_{n-1}) p(Xn∣Yn)=p(Yn)p(Yn∣Xn)p(Xn)=p(yn∣Yn−1)p(Yn−1)p(yn,Yn−1∣Xn)p(Xn)=p(yn∣Yn−1)p(Yn−1)p(yn∣Xn,Yn−1)p(Yn−1∣Xn)p(Xn)=p(yn∣Yn−1)p(yn∣Xn,Yn−1)p(Xn∣Yn−1)=p(yn∣Yn−1)p(yn∣Xn,Yn−1)p(xn∣Xn−1,Yn−1)p(Xn−1∣Yn−1)=p(yn∣Yn−1)p(yn∣xn)p(xn∣xn−1)p(Xn−1∣Yn−1)∝p(yn∣xn)p(xn∣xn−1)p(Xn−1∣Yn−1)
需要注意这里面的字母大小写所代表的不同含义,在最开始我们已经声明。
p ( y n ∣ Y n − 1 ) 为 归 一 化 常 数 p ( y n ∣ Y n − 1 ) = ∫ p ( y n ∣ x n ) p ( x n ∣ Y n − 1 ) d x n p(y_{n}|Y_{n-1}) 为归一化常数 p(y_{n}|Y_{n-1}) = \int p(y_{n}|x_{n})p(x_{n}|Y_{n-1})\,dx_{n} p(yn∣Yn−1)为归一化常数p(yn∣Yn−1)=∫p(yn∣xn)p(xn∣Yn−1)dxn
关于以下这步推导的理解: p ( y n ∣ X n , Y n − 1 ) p ( x n ∣ X n − 1 , Y n − 1 ) = p ( y n ∣ x n ) p ( x n ∣ x n − 1 ) p(y_{n}|X_{n},Y_{n-1})p(x_{n}|X_{n-1},Y_{n-1}) = p(y_{n}|x_{n})p(x_{n}|x_{n-1}) p(yn∣Xn,Yn−1)p(xn∣Xn−1,Yn−1)=p(yn∣xn)p(xn∣xn−1)
这里面有非常重要的两点需要注意也是上面声明所强调的:状态系统是一个一阶马尔可夫过程,也就是 x n x_{n} xn的状态只与 x n − 1 x_{n-1} xn−1有关。观测值 y n y_{n} yn只与 x n x_{n} xn有关,由观测模型定义。所以这样上式就很容易理解了:
在 p ( y n ∣ X n , Y n − 1 ) p(y_{n}|X_{n},Y_{n-1}) p(yn∣Xn,Yn−1)中, X n − 1 X_{n-1} Xn−1与 Y n − 1 Y_{n-1} Yn−1并不给 y n y_{n} yn提供信息量,所以该项等于 p ( y n ∣ x n ) p(y_{n}|x_{n}) p(yn∣xn)
在 p ( x n ∣ X n − 1 , Y n − 1 ) p(x_{n}|X_{n-1},Y_{n-1}) p(xn∣Xn−1,Yn−1)中,同理, Y n − 1 Y_{n-1} Yn−1和 X n − 2 X_{n-2} Xn−2不给 x n x_{n} xn提供信息量,所以该项等于 p ( x n ∣ x n − 1 ) p(x_{n}|x_{n-1}) p(xn∣xn−1)
下面继续进行粒子权值的递归推导,过程如下:
w n ( i ) ∝ p ( X n ( i ) ∣ Y n ( i ) ) q ( X n ( i ) ∣ Y n ( i ) ) = p ( y n ( i ) ∣ x n ( i ) ) p ( x n ( i ) ∣ x n − 1 ( i ) ) p ( X n − 1 ( i ) ∣ Y n − 1 ( i ) ) q ( X n − 1 ( i ) ∣ Y n − 1 ( i ) ) q ( x n ( i ) ∣ X n − 1 ( i ) , Y n ( i ) ) = w n − 1 ( i ) p ( y n ( i ) ∣ x n ( i ) ) p ( x n ( i ) ∣ x n − 1 ( i ) ) q ( x n ( i ) ∣ X n − 1 ( i ) , Y n ( i ) ) w_{n}^{(i)} \propto \frac{p(X_{n}^{(i)}|Y_{n}^{(i)})}{q(X_{n}^{(i)}|Y_{n}^{(i)})} \\ = \frac{p(y_{n}^{(i)}|x_{n}^{(i)})p(x_{n}^{(i)}|x_{n-1}^{(i)})p(X_{n-1}^{(i)}|Y_{n-1}^{(i)})}{q(X_{n-1}^{(i)}|Y_{n-1}^{(i)})q(x_{n}^{(i)}|X_{n-1}^{(i)},Y_{n}^{(i)}) }\\ =w_{n-1}^{(i)} \frac{p(y_{n}^{(i)}|x_{n}^{(i)})p(x_{n}^{(i)}|x_{n-1}^{(i)})}{q(x_{n}^{(i)}|X_{n-1}^{(i)},Y_{n}^{(i)}) } wn(i)∝q(Xn(i)∣Yn(i))p(Xn(i)∣Yn(i))=q(Xn−1(i)∣Yn−1(i))q(xn(i)∣Xn−1(i),Yn(i))p(yn(i)∣xn(i))p(xn(i)∣xn−1(i))p(Xn−1(i)∣Yn−1(i))=wn−1(i)q(xn(i)∣Xn−1(i),Yn(i))p(yn(i)∣xn(i))p(xn(i)∣xn−1(i))
当然,这里的推导是没有进行归一化的,我们实际使用的时候需要使用下式进行归一化:
w n ( i ) = w n ( i ) Σ w n ( i ) w_{n}^{(i)} = \frac{w_{n}^{(i)} }{\Sigma w_{n}^{(i)} } wn(i)=Σwn(i)wn(i)
接下来,我们寻找一个合适的重要性概率密度函数:
q ( x n ∣ X n − 1 , Y n ) = q ( x n ∣ x n − 1 , y n ) q(x_{n}|X_{n-1},Y_{n}) = q(x_{n}|x_{n-1}, y_{n}) q(xn∣Xn−1,Yn)=q(xn∣xn−1,yn)
即重要性分布的 x n x_{n} xn只与 x n − 1 x_{n-1} xn−1和 y n y_{n} yn有关,则:
w n ( i ) ∝ w n − 1 ( i ) p ( y n ( i ) ∣ x n ( i ) ) p ( x n ( i ) ∣ x n − 1 ( i ) ) q ( x n ( i ) ∣ x n − 1 ( i ) , y n ( i ) ) w_{n}^{(i)} \propto w_{n-1}^{(i)} \frac{p(y_{n}^{(i)}|x_{n}^{(i)})p(x_{n}^{(i)}|x_{n-1}^{(i)})}{q(x_{n}^{(i)}|x_{n-1}^{(i)},y_{n}^{(i)}) } wn(i)∝wn−1(i)q(xn(i)∣xn−1(i),yn(i))p(yn(i)∣xn(i))p(xn(i)∣xn−1(i))
所以,我们根据以上的推导,我们就可以总结出序贯重要性采样算法:
[ { x n ( i ) , w n ( i ) } i = 1 N ] = S I S ( { x n − 1 ( i ) , w n − 1 ( i ) } i = 1 N , Y n ) [\{x_{n}^{(i)},w_{n}^{(i)}\}_{i=1}^{N}] = SIS(\{x_{n-1}^{(i)},w_{n-1}^{(i)}\}_{i=1}^{N},Y_{n}) [{xn(i),wn(i)}i=1N]=SIS({xn−1(i),wn−1(i)}i=1N,Yn)
for i = 1 : N i = 1:N i=1:N
采样:从重要性概率密度函数中采集样本 x n ( i ) x_{n}^{(i)} xn(i)
计算:根据最新的观测计算权值 w n ( i ) w_{n}^{(i)} wn(i)
end
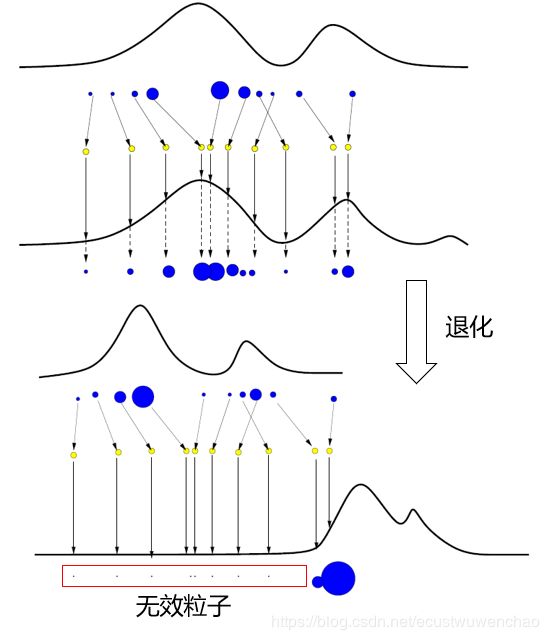
权值归一化,计算估计目标状态。这就是一个基本的序贯重要性采样的推导和算法流程了,但随着时间的推移,会出现权值退化现象,如图2所示:一些粒子的权值会变得非常小,但每次都会占用资源,这样导致大量的计算时间浪费在这些不重要的粒子上,导致估计性能下降。
一般用有效粒子数 N e f f N_{eff} Neff来衡量粒子权值的退化程度,有:
N e f f = N 1 + V a r ( w n ∗ ( i ) ) N_{eff} = \frac{N}{1+Var(w_{n}^{*(i)})} Neff=1+Var(wn∗(i))N
w n ∗ ( i ) = p ( x n ( i ) ∣ Y n ) q ( x n ( i ) ∣ x n − 1 ( i ) , Y n ) w_{n}^{*(i)} = \frac{p(x_{n}^{(i)}|Y_{n})}{q(x_{n}^{(i)}|x_{n-1}^{(i)},Y_{n})} wn∗(i)=q(xn(i)∣xn−1(i),Yn)p(xn(i)∣Yn)
上式的意思是:有效的粒子越少,权重方差越大,权值退化越严重。我们在实际计算中,有效粒子近似为:
N ˉ e f f ≈ 1 Σ i = 1 n ( w n ( i ) ) 2 \bar N_{eff} \approx \frac{1}{\Sigma_{i=1}^{n}}(w_{n}^{(i)})^2 Nˉeff≈Σi=1n1(wn(i))2
我们在进行序贯重要性采样的时候,若 N ˉ e f f \bar N_{eff} Nˉeff小于某一设定好的阈值,则应当采取一些措施加以控制。克服序贯重要性采样算法权值退化现象最直接的方法是增加粒子数,而这会造成计算量的相应增加,影响计算的实时性。因此,一般采用以下两种途径: (1)选择合适的重要性概率密度函数;(2)在序贯重要性采样之后,采用重采样方法
1.5 重采样 (Resampling)
重采样,简单来说,就是舍弃权值较小的粒子,用新的粒子来代替他们,容易想到的就是将权值较大的粒子多复制几个出来代替它们,复制的原则就是根据权重按比例进行分配。
根据前面的推导我们知道:
p ( x n ∣ Y n ) = Σ i = 1 N w n ( i ) δ ( x n − x n ( i ) ) p(x_{n}|Y_{n}) = \Sigma_{i=1}^{N}w_{n}^{(i)}\delta(x_{n}-x_{n}^{(i)}) p(xn∣Yn)=Σi=1Nwn(i)δ(xn−xn(i))
我们希望经过重采样以后得到如下结果:
p ˉ ( x n ∣ Y n ) = Σ j = 1 N 1 N δ ( x n − x n ( j ) ) = Σ k = 1 N ′ n ( k ) N ′ δ ( x n − x n ( k ) ) \bar p(x_{n}|Y_{n}) =\Sigma_{j=1}^{N}\frac{1}{N}\delta(x_{n}-x_{n}^{(j)}) = \Sigma_{k=1}^{N^{'}}\frac{n^{(k)}}{N^{'}}\delta(x_{n}-x_{n}^{(k)}) pˉ(xn∣Yn)=Σj=1NN1δ(xn−xn(j))=Σk=1N′N′n(k)δ(xn−xn(k))
上式符号较多,说明如下:
x n ( j ) x_{n}^{(j)} xn(j)表示的是从重要性密度函数中采样得到的粒子,j表示其序号,N表示其个数。
x n ( k ) x_{n}^{(k)} xn(k)表示的是重采样以后留下来的不同的粒子,k表示其序号, N ′ N^{'} N′表示其个数,而每一个 x n ( k ) x_{n}^{(k)} xn(k)由于重采样,它的个数为 n ( k ) n^{(k)} n(k),但是所有粒子的总数加起来仍然为N。
重采样策略包括固定时间间隔重采样与根据粒子权值进行的动态重采样。动态重采样通常根据当前的有效粒子数或最大与最小权值比来判断是否需要进行重采样。常用的重采样方法包括多项式(Multinomial resampling)重采样、残差重采样(Residual resampling)、分层重采样(Stratified resampling)与系统重采样(Systematic resampling)等。****残余重采样法具有效率高、实现方便的
特点,下面对此进行介绍。
残差重采样流程如下:
1.计算当前概率累计和,也就是概率分布,为 λ i , i = { 1 , 2 , … , N } \lambda _{i} ,i = \{1, 2, \ldots,N\} λi,i={1,2,…,N}
2.生成N个在个[0,1]区间均匀分布的随机数 μ j , j = { 1 , 2 , … , N } \mu_{j}, j = \{1, 2, \ldots,N\} μj,j={1,2,…,N}
3.对于每个 μ j \mu_{j} μj,寻找概率分布中大于或等于 μ j \mu_{j} μj的最小标号m,即 λ m − 1 < μ j < λ m \lambda_{m-1} < \mu_{j} <\lambda_{m} λm−1<μj<λm。当 μ j \mu_{j} μj落在该区间时,那么 x n ( m ) x_{n}^{(m)} xn(m)被复制一次,最后每个粒子的个数就是这里累计复制的个数。
举个例子:
假设当前有5个粒子,权值分别为:0.1,0.15,0.2,0.25,0.3
那么当前的概率分布为:0.1,0.25,0.45,0.7,1.0
生成5个在[0,1]中均匀分布的随机数,假设为:0.06,0.27,0.48,0.76,0.89
μ 1 = 0.06 \mu_{1} = 0.06 μ1=0.06,m=1,复制一次;
μ 2 = 0.27 \mu_{2} = 0.27 μ2=0.27,m=3,复制一次;
μ 3 = 0.48 \mu_{3} = 0.48 μ3=0.48,m=4,复制一次;
μ 4 = 0.76 \mu_{4} = 0.76 μ4=0.76,m=5,复制一次;
μ 5 = 0.89 \mu_{5} = 0.89 μ5=0.89,m=5,复制一次;
1.6 粒子滤波算法完整流程
将重采样的方法放入之前的SIS算法中,便形成了基本粒子滤波算法。
一个基本的粒子滤波算法的完整流程如下:
- 粒子集初始化,对 k = 0 k=0 k=0:
对于 i = 1 , 2 , … , N i = 1,2,\ldots,N i=1,2,…,N,由 p ( x 0 ) p(x_{0}) p(x0)生成采样粒子 x 0 ( i ) , i = 1 , 2 , … , N x_{0}^{(i)},i = 1,2,\ldots,N x0(i),i=1,2,…,N - 对于 k = 1 , 2 , 3 , … k = 1,2,3,\ldots k=1,2,3,…,执行下面的步骤:
重要性采样:从重要性概率密度函数中采集样本 x ˉ k ( i ) , i = 1 , 2 , … , N \bar x_{k}^{(i)},i = 1,2,\ldots,N xˉk(i),i=1,2,…,N,计算他们的权值 w k ( i ) w_{k}^{(i)} wk(i)并归一化
重采样:对上一步得到的粒子集 x ˉ k ( i ) , w k ( i ) {\bar x_{k}^{(i)},w_{k}^{(i)}} xˉk(i),wk(i)进行重采样,得到新的粒子集为 { x k ( i ) , 1 N } \{x_{k}^{(i)},\frac{1}{N}\} {xk(i),N1}
输出结果:计算k时刻的状态估计值
参考
[1] http://www.cnblogs.com/ycwang16/p/5995702.html
[2] https://www.cnblogs.com/aipiano/p/9060054.html
[3] https://blog.csdn.net/piaoxuezhong/article/details/78619150
[4] https://zhuanlan.zhihu.com/p/26783371
[5] 百度文库 《粒子滤波理论》