Bayesian Sparse Topical Coding 贝叶斯稀疏主题编码

摘要：稀疏主题模型(STMs)主要通过在主题模型上添加稀疏先验或适当的正则化因子，广泛用于大规模学习语义丰富的短文本潜在稀疏表示。然而，由于这些STMs的稀疏先验往往不能实现真正的稀疏，且正则化器忽略了稀疏系数之间相关性的先验信息，因此很难准确地对语料库的稀疏结构和模式进行建模。本文在稀疏群稀疏局部编码的基础上，提出了一种新的贝叶斯分层主题模型——泊松分布贝叶斯稀疏局部编码(BSTC-P)。与传统的STMs不同，它侧重于利用稀疏系数之间的相关先验信息，在稀疏系数之间施加分层稀疏。此外，我们提出了一种稀疏增强的BSTC，即贝叶斯稀疏正态分布局部编码(BSTC- n)。我们采用优越的分层稀疏诱导先验，以达到最稀疏的最优解。对新闻组和Twitter数据集的实验结果表明，BSTC-P和BSTC-N在寻找清晰的潜在语义表示方面都有较好的性能。因此，与现有的文档分类任务相比，它们具有更好的性能

1. 简介

随着社交网络的发展，对于很多互联网用户来说短文本以成为很重要的信息源，这些短文本具有传播速度快、长度短、信息量大、信息稀疏、噪声大、形态不规则等特点。由于这些特性，短文本无法通过手工和传统工具来处理。因此，迫切需要能够从大量的短文本中提取有用和有意义的潜在表示的强大工具。提取的潜在表示对后续研究和工程应用具有重要意义，如突发事件检测[13]、[20]、用户兴趣建模[21]、微博影响分析[22]、自动查询回复[58]等。潜在狄利克雷分配(LDA)[1]，[15]是一个非常有用的概率工具，用于分析大量的文本。它在超链接分析[47]和查询处理[50]等许多领域都取得了显著的进展。基于LDA的概率主题模型[2]、[3]、[4]从没有任何标签的原始语料库中学习潜在文档和主题表示。本质上，它们通过隐式捕获文档级单词共现信息[4]生成潜在表示。近些年终它们被广泛应用于具有丰富的词的共现信息的长文本分析当中。然而，短文本具有文档长度短、词汇量大、主题范围广、噪音大等特点。因此，每个简短文档中的单词共出现信息变得更加稀疏，这不可避免地影响了这些模型的性能。研究还证明，当文本的平均令牌数N过小时，基于LDA的概率主题模型不能准确地学习主题，并可能产生大部分不连贯的主题[57]。这是因为从这些模型中学习到的主题在形式上是N个共混词的多项分布，分散在不同的短文本中。表1通过在Tweets集合上直接应用LDA显示了主题词的示例。很明显，LDA学习的主题词是没有意义和不连贯的。话题2中的lauder, facebook和president这三个词实际上属于不同的话题，但是它们被不合理地分配到了同一个话题上。综上所述，直接将这些模型应用于短文本将会遇到严重的数据稀疏问题。

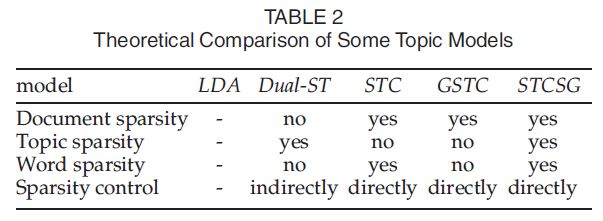
这一问题引起了人们的广泛关注，近年来出现了许多研究方法，主要有以下两个方面:利用稀疏先验[8]、[9]、[16]和施加后验正则化[11]、[12]、[23]。这两种方法都是基于要学习的潜在表示是高度稀疏的。每个文档关注几个主题，每个主题关注几个单词[12]。第一种方法在概率主题模型中引入了辅助变量，如尖峰和平板，但在控制概率主题模型(PTMs)混合比例的稀疏性方面效果不佳。第二种方法对非概率模型施加后验正则化，如lasso[10]、group lasso[6]、[24]和稀疏group lasso[5]。它们可以实现真正意义上的稀疏表示。这两次尝试都能够找到完整的稀疏表示[14]、[16]，它们比传统主题模型生成的表示更具有可解释性、清晰性和意义。为了便于比较，我们在表2中报告了五个密切相关模型的一些理论特性。虽然上述两种方法取得了较好的性能，但仍存在一些挑战:(1)第一种方法未能实现真正意义上的稀疏表示，(2)第二种方法考虑稀疏系数之间相关性的先验信息较少。

该方法基于我们最近使用稀疏组(STCSG)[16]进行稀疏主题编码的工作。STCSG是通过引入稀疏先验来发现大数据集合的潜在表示形式的主题模型的非概率表达式。通过引入稀疏组，STCSG放宽了推理表示的规范化约束，能够有效地对单词、主题和文档代码的稀疏性进行建模。然而，STCSG使用传统的稀疏诱导正则化方法，绕过了稀疏系数之间相关的先验信息。针对STCSG的上述挑战和不足，我们提出了一种新的贝叶斯分层稀疏局部编码，即具有泊松分布的贝叶斯稀疏局部编码(BSTC-P)，它是STCSG本质上的贝叶斯扩展，在利用稀疏解的结构信息方面具有较大的灵活性。它可以学习更稀疏、更有意义的表示，并尽可能利用与一个主题关联强、与其他主题关联弱的关键词，形成了表达主题语义的优秀能力。针对STCSG的上述挑战和不足，我们提出了一种新的贝叶斯分层稀疏局部编码，即具有泊松分布的贝叶斯稀疏局部编码(BSTC-P)，它是STCSG本质上的贝叶斯扩展，在利用稀疏解的结构信息方面具有较大的灵活性。它可以学习更稀疏、更有意义的表示，并尽可能利用与一个主题关联强、与其他主题关联弱的关键词，形成了表达主题语义的优秀能力。BSTC-P利用泊松分布对离散词数进行建模，利用Gamma- Jeffrey分布对关键词在词汇表中的概率分布、关键词语义空间中主题的概率分布以及主题基进行建模。通过使用层次拉普拉斯先验，它可以发现比使用非层次稀疏先验和传统稀疏诱导正则化的STMs更紧凑、更有效的编码。但是，由于将Gamma分布作为稀疏解的先验分布，会影响BSTC-P的收敛性，所以仍然没有找到最稀疏的最优解。

Therefore, we propose the sparsityenhanced BSTC, Bayesian Sparse Topical Coding with Normal Distribution (BSTC-N), which utilizes Normal distribution to model word count, and incorporates zero mean Normal-Jeffrey prior to model probability distributions of keyword in the vocabulary, probability distributions of topics in the keywords semantic space, and the topic basis.

因此,我们建议sparsityenhanced BSTC,贝叶斯稀疏局部编码与正态分布(BSTC-N),字数,利用正态分布模型,并结合零均值Normal-Jeffrey之前模型概率分布的关键字在词汇表中,概率分布的主题关键字语义空间,基础和主题。

一般来说，对于BSTC-N，它比BSTC-P更有可能获得最稀疏的最优解，并且能够实现更稀疏、更有意义的潜在表示。注意到不适合对文本和离散数据建模。

The main contributions of this paper are listed as follows:

本文的主要贡献如下

 1) To the best of our knowledge, we are the first one to employ sparse hierarchical prior for sparse topical coding.We design a novel Bayesian hierarchical topic model BSTC-P, to obtain more accurate and effective document, topic and word-level sparsity by introducing sparse Bayesian learning.

1)据我们所知，我们是第一个使用稀疏层次先验进行稀疏局部编码的。我们设计了一种新的贝叶斯层次主题模型BSTC-P，通过引入稀疏贝叶斯学习来获得更准确、更有效的文档、主题和单词级稀疏性。

In order to derive the sparsest optimal solution and more compact sparse representations further, we propose a novel Bayesian hierarchical topic model BSTC-N.

为了进一步得到最稀疏的最优解和更紧凑的稀疏表示，我们提出了一种新的贝叶斯层次主题模型BSTC-N。

2) We incorporate the Expectation Maximization algorithm (EM) and Variational Inference to efficiently approximate the posterior of these two models.

我们将期望最大化算法(EM)和变分推理相结合，有效地逼近了这两个模型的后验。

3) We evaluate the effectiveness and efficiency of our models by conducting experiments on 20 Newsgroups and Twitter dataset. Experimental results show that these two models outperform other baselines.

通过对20个新闻组和Twitter数据集进行实验，评估模型的有效性和效率。实验结果表明，这两种模型均优于其他基线。

2. 相关工作

关于稀疏主题模型的研究已经有很多，目的是获得稀疏的潜在表示。我们的工作与以下几方面的研究有关。

2.1 稀疏增强的概率主题模型 Sparsity-PTMs

有许多稀疏增强的概率主题模型，其目的是通过对基于ldap的模型施加稀疏先验，提取有意义的潜在单词、主题和文档表示。Wang等人[25]、[26]提出了聚焦主题模型(focus topic model, FTM)，通过使用从IBP中抽取的稀疏二进制矩阵来增强潜在文档表示的稀疏性，从而学习稀疏主题混合模式。基于FTM, Chen等人[27]通过利用作者和文档地点的上下文信息提出了cFTM，其中使用分层beta过程来推断与每个作者和地点相关的重点主题集。Archambeau等人[28]提出了IBP- lda，其中使用四参数IBP复合Dirichlet过程(ICDP)来解释大型文本语料库中存在的大量主题以及自然语言词汇的幂律分布。与IBP-LDA类似，在对文档-主题和主题词分布的稀疏性和平滑性进行解耦之前，利用峰和板提出了双sparseTM[12]。Doshi-Velez等人通过利用单词之间关系的知识构建了图稀疏LDA，其中主题由一些潜在的概念(来自解释所观察单词的底层图中的单词)总结。Kujala[29]在LDA的基础上提出稀疏主题模型ldl -CCCP，利用凹凸过程(CCCP)对LDA目标进行优化，生成稀疏模型。但上述方法均缺乏直接控制后验稀疏性的能力。

2.2 稀疏增强的非概率主题模型 Sparsity-NPTMs

也有一些非概率稀疏主题模型[8]、[9]、[16]可以通过施加lasso、group lasso和稀疏group lasso等正则化器来直接控制稀疏性。矩阵分解(如[7]、[30]、[31])等方法将主题建模形式化，将其作为lasso、group lasso等正则化的损失函数最小化的问题。但是，通过这些模型学习到的表示通常是非正的。此外，将稀疏编码引入到非概率主题模型中。Zhu等人利用混合正则化器提出了稀疏局部编码(STC)，用于发现大量数据集合的潜在表示形式。然而，STC不能发现组稀疏模式。Bai等人通过引入组稀疏，设计了组稀疏局部编码(GSTC)，其性能优于STC。但是它们无法实现每个文档、每个主题和每个术语的主题完全稀疏。随后，Peng等人[16]提出了稀疏的主题编码，用稀疏的组来寻找文本的潜在单词、主题和文档表示。Than等人[14]提出了全稀疏主题模型(full - Sparse Topic Model, FSTM)，该模型能够快速学习稀疏主题，推断出文档的稀疏潜在表示形式，显著节省存储内存。与PTMs不同，它们成功地直接实现了真正意义上的稀疏后验表示。然而，它们仍然没有利用稀疏系数之间的相关先验信息。

2.3 稀疏贝叶斯学习

为了获得回归和分类任务的稀疏解，提出了一种基于Tipping[32]的稀疏贝叶斯学习方法。从那时起，SBL被广泛应用于压缩感知(CS)，如[33]、[35]、[36]。与传统的利用lasso的CS方法不同，即使传感矩阵的列之间存在很强的相关性，这些方法也具有良好的性能。Wipf等人[33]将SBL cost函数作为一种工具，用于从过完备的字典中寻找信号的稀疏表示。该SBL框架保留了lasso分集测量的理想特性，并能够通过使用Jeffreys super prior获得更稀疏的解决方案。这是一个参数空间的非信息先验分布，在贝叶斯分析[36]、[44]中得到了广泛的应用。[34]、[35]利用先验分布的层次形式对具有高度稀疏性的未知信号的稀疏性进行建模。Chien等人提出了一种新的基于LDA的稀疏主题建模的贝叶斯稀疏学习方法。此外，Minjung等人对[37]提出了充分的建议lassos的贝叶斯公式。与传统的惩罚算法相比稀疏贝叶斯学习有很多明显的优点:1)在没有噪声[38]的情况下，基于l1的算法的全局最小值并不是真正的最稀疏解。然而，稀疏贝叶斯学习恰恰相反，是一种更好的[33]替代方法;2)证明了稀疏贝叶斯学习等价于迭代重加权L1最小化[39]。同时指出，利用迭代重加权L1极小化可以很容易地得到真正的最稀疏解。在我们的工作中，我们通过使用SBL来提出BSTC-P，以获得更稀疏和更有意义的表示。一方面可以直接控制后壁稀疏性，如稀疏nptms;另一方面，它可以像sparse- ptms那样推断稀疏文档、主题和单词的比例。此外，通过数学逼近，利用零均值正态-杰弗里斯递阶先验，得到了BSTC-N中最稀疏的最优解。