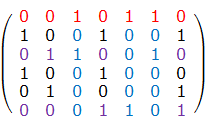使用dancing links算法求解数独

使用dancing links算法求解数独

博文来自这里:http://www.cnblogs.com/grenet/p/3145800.html
以及http://www.cnblogs.com/grenet/p/3163550.html

算法的实现来自https://github.com/chenshuo/recipes/tree/master/sudoku

我这里只是解读了一下代码,备忘.

精确覆盖问题的定义

给定一个由0-1组成的矩阵，是否能找到一个行的集合，使得集合中每一列都恰好包含一个1.

例如：如下的矩阵:

矩阵

就包含了这样一个集合(第1、4、5行).

如何利用给定的矩阵求出相应的行的集合呢？我们可以采用回溯法.

假定给定如下的矩阵(矩阵1):

矩阵1

先假定选择第1行，如下所示：

选定第1行

如上图中所示，红色的那行是选中的一行，这一行中有3个1，分别是第3、5、6列。

由于这3列已经包含了1，故，把这三列往下标示，图中的蓝色部分。蓝色部分包含3个1，分别在2行中，把这2行用紫色标示出来.

根据定义，同一列的1只能有1个，故紫色的两行，和红色的一行的1相冲突。

那么在接下来的求解中，红色的部分、蓝色的部分、紫色的部分都不能用了，把这些部分都删除，可以得到一个新的矩阵(矩阵2):

矩阵2

行分别对应矩阵1中的第2、4、5行.

列分别对应矩阵1中的第1、2、4、7列.

于是问题就转换为一个规模小点的精确覆盖问题.

在新的矩阵中再选择第1行，如下图所示:

矩阵2

还是按照之前的步骤，进行标示。红色、蓝色和紫色的部分又全都删除，导致新的空矩阵产生，而红色的一行中有0（有0就说明这一列没有1覆盖）。说明，第1行选择是错误的.

那么回到之前，选择第2行，如下图所示:

重新选择

按照之前的步骤，进行标示。把红色、蓝色、紫色部分删除后，得到新的矩阵(矩阵3):

矩阵3

行对应矩阵2中的第3行，矩阵1中的第5行.

列对应矩阵2中的第2、4列，矩阵1中的第2、7列.

由于剩下的矩阵只有1行，且都是1，选择这一行，问题就解决.

于是该问题的解就是矩阵1中第1行、矩阵2中的第2行、矩阵3中的第1行。也就是矩阵1中的第1、4、5行.

在求解这个问题的过程中，我们第1步选择第1行是正确的，但是不是每个题目第1步选择都是正确的，如果选择第1行无法求解出结果出来，那么就要推倒之前的选择，从选择第2行开始，依此类推.

从上面的求解过程来看，实际上求解过程可以如下表示

1. 从矩阵中选择一行;
2. 根据定义，标示矩阵中其他行的元素;
3. 删除相关行和列的元素，得到新矩阵;
4. 如果新矩阵是空矩阵，并且之前的一行都是1，那么求解结束，跳转到6；新矩阵不是空矩阵，继续求解，跳转到1；新矩阵是空矩阵，之前的一行中有0，跳转到5;
5. 说明之前的选择有误，回溯到之前的一个矩阵，跳转到1；如果没有矩阵可以回溯，说明该问题无解，跳转到7;
6. 求解结束，把结果输出;
7. 求解结束，输出无解消息.

从如上的求解流程来看，在求解的过程中有大量的缓存矩阵和回溯矩阵的过程。而如何缓存矩阵以及相关的数据（保证后面的回溯能正确恢复数据），也是一个比较头疼的问题（并不是无法解决）。以及在输出结果的时候，如何输出正确的结果（把每一步的选择转换为初始矩阵相应的行）。

于是算法大师Donald E.Knuth（《计算机程序设计艺术》的作者）出面解决了这个方面的难题。他提出了DLX（Dancing Links X）算法。实际上，他把上面求解的过程称为X算法，而他提出的舞蹈链（Dancing Links）实际上并不是一种算法，而是一种数据结构。一种非常巧妙的数据结构，他的数据结构在缓存和回溯的过程中效率惊人，不需要额外的空间，以及近乎线性的时间。而在整个求解过程中，指针在数据之间跳跃着，就像精巧设计的舞蹈一样，故Donald E.Knuth把它称为Dancing Links（中文译名舞蹈链）。

Dancing Links的核心是基于双向链的方便操作（移除、恢复加入）.

我们用例子来说明.

假设双向链的三个连续的元素，A1、A2、A3，每个元素有两个分量Left和Right，分别指向左边和右边的元素。由定义可知

A1.Right = A2, A2.Right = A3;
A2.Left = A1, A3.Left = A2;

在这个双向链中，可以由任一个元素得到其他两个元素，A1.Right.Right = A3, A3.Left.Left = A1等等.

现在把A2这个元素从双向链中移除（不是删除）出去，那么执行下面的操作就可以了:

A1.Right = A3, A3.Left = A1;

那么就直接连接起A1和A3。A2从双向链中移除出去了。但仅仅是从双向链中移除了，A2这个实体还在，并没有删除。只是在双向链中遍历的话，遍历不到A2了。

那么A2这个实体中的两个分量Left和Right指向谁？由于实体还在，而且没有修改A2分量的操作，那么A2的两个分量指向没有发生变化，也就是在移除前的指向。即A2.Left = A1和A2.Right = A3.

如果此时发现，需要把A2这个元素重新加入到双向链中的原来的位置，也就是A1和A3的中间。由于A2的两个分量没有发生变化，仍然指向A1和A3。那么只要修改A1的Right分量和A3的Left就行了。也就是下面的操作:

A1.Right = A2, A3.Left = A2;

仔细想想，上面两个操作（移除和恢复加入）对应了什么？是不是对应了之前的算法过程中的关键的两步？

移除操作对应着缓存数据、恢复加入操作对应着回溯数据。而美妙的是，这两个操作不再占用新的空间，时间上也是极快速的

在很多实际运用中，把双向链的首尾相连，构成循环双向链表.

Dancing Links用的数据结构是交叉十字循环双向链.

而Dancing Links中的每个元素不仅是横向循环双向链中的一份子，又是纵向循环双向链的一份子。

因为精确覆盖问题的矩阵往往是稀疏矩阵（矩阵中，0的个数多于1），Dancing Links仅仅记录矩阵中值是1的元素。

Dancing Links中的每个元素一般而言,有6个分量。分别是--Left指向左边的元素、Right指向右边的元素、Up指向上边的元素、Down指向下边的元素、Col指向列标元素、Row指示当前元素所在的行。

Dancing Links还要准备一些辅助元素（为什么需要这些辅助元素？没有太多的道理，大师认为这能解决问题，实际上是解决了问题）：

Ans()：Ans数组，在求解的过程中保留当前的答案，以供最后输出答案用。

Head元素：求解的辅助元素，在求解的过程中，当判断出Head.Right = Head （也可以是Head.Left = Head）时，求解结束，输出答案。Head元素只有两个分量有用。其余的分量对求解没啥用。

C元素：辅助元素，称列标元素，每列有一个列标元素。本文开始的题目的列标元素分别是C1、C2、C3、C4、C5、C6、C7。每一列的元素的Col分量都指向所在列的列标元素。列标元素的Col分量指向自己（也可以是没有）。在初始化的状态下，Head.Right = C1, C1.Right = C2, ..., C7.Right = Head, Head.Left = C7等等。列标元素的分量Row = 0，表示是处在第0行。

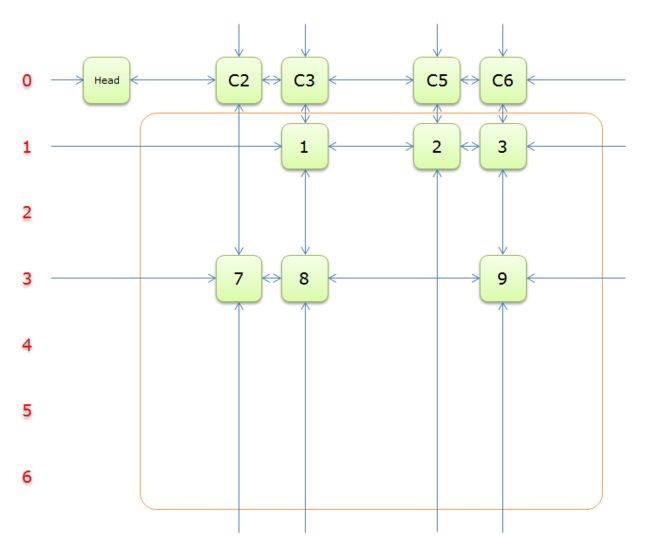
下图就是根据题目构建好的交叉十字循环双向链（构建的过程后面的详述）.

交叉十字循环双向链

就上图解释一下：

每个绿色方块是一个元素，其中Head和C1、C2、...、C7是辅助元素。橙色框中的元素是原矩阵中1的元素，给他们标上号（从1到16）.

左侧的红色，标示的是行号，辅助元素所在的行是0行，其余元素所在的行从1到6。

每两个元素之间有一个双向箭头连线，表示双向链中相邻两个元素的关系（水平的是左右关系、垂直的是上下关系）。

单向的箭头并不是表示单向关系，而因为是循环双向链，左侧的单向箭头和右侧的单向箭头（上边的和下边的）组成了一个双向箭头，例如元素14左侧的单向箭头和元素16右侧的单项箭头组成一个双向箭头，表示14.Left=16、16.Right=14；同理，元素14下边的单项箭头和元素C4上边的单向箭头组成一个双向箭头，表示14.Down=C4、C4.Up=14。

接下来，利用图来解释Dancing Links是如何求解精确覆盖问题。

1. 首先判断Head.Right=Head？若是，求解结束，输出解；若不是，求解还没结束，到步骤2（也可以判断Head.Left=Head？）

2. 获取Head.Right元素，即元素C1，并标示元素C1（标示元素C1，指的是标示C1、和C1所在列的所有元素、以及该元素所在行的元素，并从双向链中移除这些元素）。如下图中的紫色部分。
   

   

   交叉十字循环双向链
   
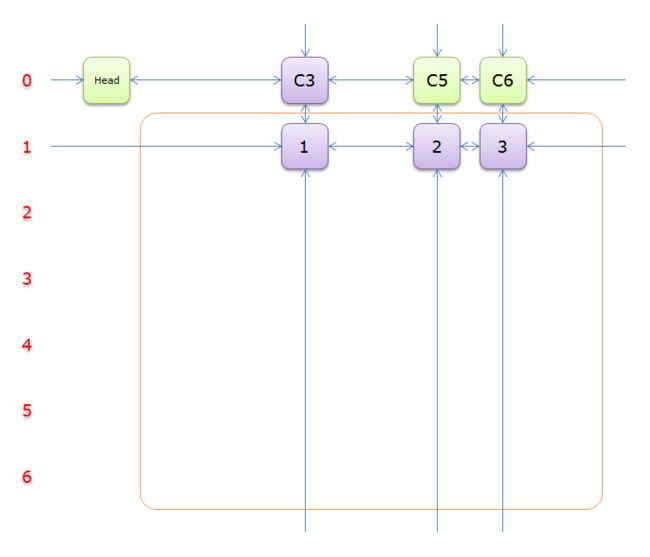
   如上图可知，行2和行4中的一个必是答案的一部分（其他行中没有元素能覆盖列C1），先假设选择的是行2.

3. 选择行2（在答案栈中压入2），标示该行中的其他元素（元素5和元素6）所在的列首元素，即标示元素C4和标示元素C7，下图中的橙色部分。
   注意的是，即使元素5在步骤2中就从双向链中移除，但是元素5的Col分量还是指向元素C4的，这里体现了双向链的强大作用。
   

   

   交叉十字循环双向链
   
   把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:
   
   

   交叉十字循环双向链
   
   一下子空了好多，是不是转换为一个少了很多元素的精确覆盖问题？，利用递归的思想，很快就能写出求解的过程来。我们继续完成求解过程

4. 获取Head.Right元素，即元素C2，并标示元素C2。如下图中的紫色部分。
   

   

   交叉十字循环双向链
   
   如图，列C2只有元素7覆盖，故答案只能选择行3.

5. 选择行3（在答案栈中压入3），标示该行中的其他元素（元素8和元素9）所在的列首元素，即标示元素C3和标示元素C6，下图中的橙色部分。
   

   

   交叉十字循环双向链
   
   把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:
   
   

   交叉十字循环双向链

6. 获取Head.Right元素，即元素C5，元素C5中的垂直双向链中没有其他元素，也就是没有元素覆盖列C5。说明当前求解失败。要回溯到之前的分叉选择步骤（步骤2）。那要回标列首元素（把列首元素、所在列的元素，以及对应行其余的元素。并恢复这些元素到双向链中），回标列首元素的顺序是标示元素的顺序的反过来。从前文可知，顺序是回标列首C6、回标列首C3、回标列首C2、回标列首C7、回标列首C4。表面上看起来比较复杂，实际上利用递归，是一件很简单的事。并把答案栈恢复到步骤2（清空的状态）的时候。又回到下图所示:
   

   

   交叉十字循环双向链表

7. 由于之前选择行2导致无解，因此这次选择行4（再无解就整个问题就无解了）。选择行4（在答案栈中压入4），标示该行中的其他元素（元素11）所在的列首元素，即标示元素C4，下图中的橙色部分。
   

   

   交叉十字循环双向链表
   
   把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:
   
   

   交叉十字循环双向链表

8. 获取Head.Right元素，即元素C2，并标示元素C2。如下图中的紫色部分。
   

   

   交叉十字循环双向链
   
   如图，行3和行5都可以选择

9. 选择行3（在答案栈中压入3），标示该行中的其他元素（元素8和元素9）所在的列首元素，即标示元素C3和标示元素C6，下图中的橙色部分。
   

   

   交叉十字循环双向链表
   
   把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:
   
   

   交叉十字循环双向链

10. 获取Head.Right元素，即元素C5，元素C5中的垂直双向链中没有其他元素，也就是没有元素覆盖列C5。说明当前求解失败。要回溯到之前的分叉选择步骤（步骤8）。从前文可知，回标列首C6、回标列首C3。并把答案栈恢复到步骤8（答案栈中只有4）的时候。又回到下图所示:
    

    

    交叉十字循环双向链表

11. 由于之前选择行3导致无解，因此这次选择行5（在答案栈中压入5），标示该行中的其他元素（元素13）所在的列首元素，即标示元素C7，下图中的橙色部分。
    

    

    交叉十字循环双向链
    
    把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:
    
    

    交叉十字循环双向链

12. 获取Head.Right元素，即元素C3，并标示元素C3。如下图中的紫色部分。
    

    

    交叉十字循环双向链

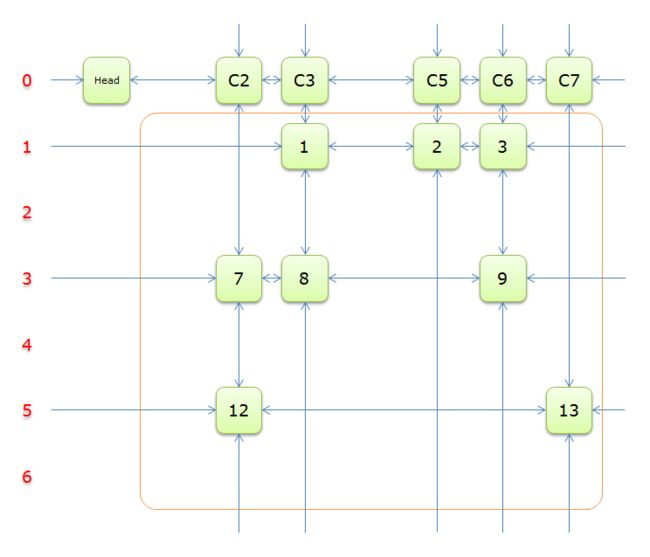
13. 如上图，列C3只有元素1覆盖，故答案只能选择行3（在答案栈压入1）。标示该行中的其他元素（元素2和元素3）所在的列首元素，即标示元素C5和标示元素C6，下图中的橙色部分。
    

    

    交叉十字循环双向链表
    
    把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示:
    
    

    交叉十字循环双向链

14. 因为Head.Right=Head。故，整个过程求解结束。输出答案，答案栈中的答案分别是4、5、1。表示该问题的解是第4、5、1行覆盖所有的列。如下图所示（蓝色的部分）:
    

    

    交叉十字循环双向链

从以上的14步来看，可以把Dancing Links的求解过程表述如下

1. Dancing函数的入口
2. 判断Head.Right=Head？，若是，输出答案，返回True，退出函数。
3. 获得Head.Right的元素C
4. 标示元素C
5. 获得元素C所在列的一个元素
6. 标示该元素同行的其余元素所在的列首元素
7. 获得一个简化的问题，递归调用Daning函数，若返回的True，则返回True，退出函数。
8. 若返回的是False，则回标该元素同行的其余元素所在的列首元素，回标的顺序和之前标示的顺序相反
9. 获得元素C所在列的下一个元素，若有，跳转到步骤6
10. 若没有，回标元素C，返回False，退出函数。

之前的文章的表述，为了表述简单，采用面向对象的思路，说每个元素有6个分量，分别是Left、Right、Up、Down、Col、Row分量。

但在实际的编码中，用数组也能实现相同的作用。例如：用Left（）表示所有元素的Left分量，Left（1）表示元素1的Left分量.

在前文中，元素分为Head元素、列首元素（C1、C2等）、普通元素。在编码中，三种元素统一成一种元素。如上题，0表示Head元素，1表示元素C1、2表示元素C2、...、7表示元素C7，从8开始表示普通元素。这是统一后，编码的简便性。利用数组的下标来表示元素，宛若指针一般。

如何利用Dancing links算法来求解数独

舞蹈链（Dancing Links）算法在求解精确覆盖问题时效率惊人。

那利用舞蹈链（Dancing Links）算法求解数独问题，实际上就是下面一个流程

1. 把数独问题转换为精确覆盖问题;
2. 设计出数据矩阵;
3. 用舞蹈链（Dancing Links）算法求解该精确覆盖问题;
4. 把该精确覆盖问题的解转换为数独的解.

数独的规则

数独（Sudoku）是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫内的数字均含1-9，不重复。 每一道合格的数独谜题都有且仅有唯一答案，推理方法也以此为基础，任何无解或多解的题目都是不合格的。

如下图所示，就是一个数独的题目:

数独

首先看看数独问题（9*9的方格）的规则

1. 每个格子只能填一个数字;
2. 每行每个数字只能填一遍,对于上面题目中的第一行,一共9个空格,但是1~9这9个数字只能出现1遍,也就是说,第1行余下的空格中,已经不能填写6,5,9,3了;
3. 每列每个数字只能填一遍,对于上面的图,第1列的其他空格已经不能填入9, 1, 4, 2了;
4. 每宫每个数字只能填一遍,所谓的宫,代表的是图中比较大的3*3的格子.

那现在就是利用这个规则把数独问题转换为精确覆盖问题。

可是，直观上面的规则，发现比较难以转换为精确覆盖问题。因此，把上面的表述换个说法。

1. 每个格子只能填一个数字；
2. 每行1-9的这9个数字都得填一遍（也就意味着每个数字只能填一遍）；
3. 每列1-9的这9个数字都得填一遍；
4. 每宫1-9的这9个数字都得填一遍。

这样理解的话，数独问题转换为精确覆盖问题就相对简单多了。关键就是如何构造精确覆盖问题中的矩阵.

我们把矩阵的每个列都定义成一个约束条件。

第1列定义成：（1，1）填了一个数字
第2列定义成：（1，2）填了一个数字
...
第9列定义成：（1，9）填了一个数字
第10列定义成：（2，1）填了一个数字
...
第18列定义成：（2，9）填了一个数字
...
第81列定义成：（9，9）填了一个数字

至此，用第1-81列完成了约束条件1：每个格子只能填一个数字

第N列（1≤N≤81）定义成：（X，Y）填了一个数字。

N、X、Y之间的关系是：X = INT((N - 1)/ 9)+1; Y = ((N-1) Mod 9) + 1; N =(X - 1) × 9 + Y.

第82列定义成：在第1行填了数字1
第83列定义成：在第1行填了数字2
...
第90列定义成：在第1行填了数字9
第91列定义成：在第2行填了数字1
...
第99列定义成：在第2行填了数字9
...
第162列定义成：在第9行填了数字9

至此，用第82-162列（共81列）完成了约束条件2：每行1-9的这9个数字都得填一遍

第N列（82≤N≤162）定义成：在第X行填了数字Y。

N、X、Y之间的关系是：X = INT(N - 81 - 1)/ 9)+ 1; Y = ((N - 81 - 1)Mod 9)+ 1; N = (X - 1)× 9 + Y + 81.

第163列定义成：在第1列填了数字1
第164列定义成：在第1列填了数字2
...
第171列定义成：在第1列填了数字9
第172列定义成：在第2列填了数字1
...
第180列定义成：在第2列填了数字9
...
第243列定义成：在第9列填了数字9

至此，用第163-243列（共81列）完成了约束条件3：每列1-9的这9个数字都得填一遍

第N列（163≤N≤243）定义成：在第X列填了数字Y。

N、X、Y之间的关系是：X = INT((N - 162 - 1) / 9) + 1; Y =((N - 162 - 1)Mod 9) + 1; N = (X - 1)× 9 + Y + 162.

第244列定义成：在第1宫填了数字1
第245列定义成：在第1宫填了数字2
...
第252列定义成：在第1宫填了数字9
第253列定义成：在第2宫填了数字1
...
第261列定义成：在第2宫填了数字9
...
第324列定义成：在第9宫填了数字9

至此，用第244-324列（共81列）完成了约束条件4：每宫1-9的这9个数字都得填一遍

第N列（244≤N≤324）定义成：在第X宫填了数字Y。

N、X、Y之间的关系是：X = INT((N - 243 - 1) / 9)+ 1; Y = ((N - 243 - 1)Mod 9)+ 1; N = (X - 1) × 9 + Y + 243.

至此，用了324列完成了数独的四个约束条件，矩阵的列定义完成.

那接下来，就是把数独转换为矩阵.

数独问题中，每个格子分两种情况。有数字的格子、没数字的格子。

有数字的格子

以例子来说明，在（4，2）中填的是7

把（4，2）中填的是7，解释成4个约束条件

1. 在（4，2）中填了一个数字。
2. 在第4行填了数字7
3. 在第2列填了数字7
4. 在第4宫填了数字7（坐标(X，Y)到宫N的公式为：N = INT((X - 1) / 3) × 3 + INT((Y - 1) / 3)+ 1).

那么这4个条件，分别转换成矩阵对应的列为

1. 在(4，2)中填了一个数字。对应的列N = (4 - 1）×9 + 2 = 29
2. 在第4行填了数字7。对应的列N = (4 - 1) × 9+ 7 + 81 = 115
3. 在第2列填了数字7。对应的列N = (2 - 1）× 9 + 7 + 162 = 178
4. 在第4宫填了数字7。对应的列N = (4 - 1)× 9 + 7 + 243 = 277

于是，(4，2)中填的是7，转成矩阵的一行就是，第29、115、178、277列是1，其余列是0。把这1行插入到矩阵中去。

没数字的格子

还是举例说明，在(5，8)中没有数字

把(5，8)中没有数字转换成:

（5，8）中填的是1，转成矩阵的一行就是，第44、118、226、289列是1，其余列是0。
（5，8）中填的是2，转成矩阵的一行就是，第44、119、227、290列是1，其余列是0。
（5，8）中填的是3，转成矩阵的一行就是，第44、120、228、291列是1，其余列是0。
（5，8）中填的是4，转成矩阵的一行就是，第44、121、229、292列是1，其余列是0。
（5，8）中填的是5，转成矩阵的一行就是，第44、122、230、293列是1，其余列是0。
（5，8）中填的是6，转成矩阵的一行就是，第44、123、231、294列是1，其余列是0。
（5，8）中填的是7，转成矩阵的一行就是，第44、124、232、295列是1，其余列是0。
（5，8）中填的是8，转成矩阵的一行就是，第44、125、233、296列是1，其余列是0。
（5，8）中填的是9，转成矩阵的一行就是，第44、126、234、297列是1，其余列是0。

把这9行插入到矩阵中。由于这9行的第44列都是1（不会有其他行的44列会是1），也就是说这9行中必只有1行（有且只有1行）选中（精确覆盖问题的定义，每列只能有1个1），是最后解的一部分。这就保证了最后解在(5，8)中只有1个数字。

这样，从数独的格子依次转换成行（1行或者9行）插入到矩阵中。完成了数独问题到精确覆盖问题的转换。

接下来求解精确覆盖问题就可以交给舞蹈链（Dancing Links）算法了.

CPP代码

实际的编码过程可能并不完全按照上面的算法进行，因为我们要加快运行的速度，以及简化编码的复杂度。

这里需要注意一下，对于上面的元素C1, C2...,我们下面统一称作表头元素，而不是列标元素。

为了方便编码,我们可以将上图中的head,表头以及每个十字链中的每一个元素统一都用Node这个结构来表示,每一个Node都长成这样:

struct Node;
typedef Node Column;
struct Node
{
    Node* left; // 每一个节点都有上下左右4个指针域
    Node* right;
    Node* up;
    Node* down;
    Column* col; // 用于指向表头元素
    int name; // 记录该元素所在列的表头元素在columns_数组中的下标
    int size; // 用于记录这一列一共有多少元素,一般这个域只供表头元素使用
};

为了完成我们的算法,我们提供了这么一些辅助的数据结构:

struct Dance
{
    Column* root_; // root_表示上面的head
    int*    inout_; // 输入的谜题
    Column* columns_[400]; // columns用于记录每一列的头部,即表头
    vector stack_; // 用于存储选择的列
    Node    nodes_[kMaxNodes]; // 我们使用数组来实现算法,事先分配好,避免new
    int     cur_node_; // 指示器,表示nodes_中已经分配了的node的数目
    ...
}

下面是一些常量的定义:

const int kMaxNodes = 1 + 81 * 4 + 9 * 9 * 9 * 4;
const int kMaxColumns = 400; // 列的数目最多不超过400个
const int kRow = 100, kCol = 200, kBox = 300;

在Dance结构体中,定义了这么一个初始化结构的构造函数,我们一步一步来分析.这里需要说明一下的是输入的数据，它是一个包含81个int型数据的数组，类似于这种形式：

000000010400000000020000000000050407008000300001090000300400200050100000000806000

0代表要填入的数字，其余的表示都已经填入。

Dance(int inout[81]) : inout_(inout), cur_node_(0) 
{ // inout表示输入的谜题,输入是一个包含81个int型数据的数组,
  //从左至右,从上到下表示了每一个格子中填的值 
  // 0表示带填入的数据,否则表示该位置已经填入了值
  // 注意cur_node_被初始化为了0,表示nodes_数组从头开始分配 
    ...
}

下面是具体的代码分析:

/* Dance结构的构造函数Dance */
stack_.reserve(100); // 事先分配好空间

root_ = new_column(); // head
root_->left = root_->right = root_;
memset(columns_, 0, sizeof(columns_));

bool rows[N][10] = { false }; // 0~9一共10个数
bool cols[N][10] = { false };
bool boxes[N][10] = { false };

我们看一下new_column函数具体干了什么?

Column* new_column(int n = 0) // 构建一个新列
{
    Column* c = &nodes_[cur_node_++]; // 分配一个节点
    memset(c, 0, sizeof(Column));
    // 让节点内所有的指针都指向自己
    c->left = c;
    c->right = c;
    c->up = c;
    c->down = c;
    c->col = c;
    c->name = n; // name用于表示该节点代表的列,0代表head
    return c;
}

我们继续来分析Dance的构造函数:

/* Dance结构的构造函数Dance */
for (int i = 0; i < N; ++i) { // N = 81 
    int row = i / 9;    // 获得第i个元素所在行
    int col = i % 9;    // 所在的列
    int box = row / 3 * 3 + col / 3;    // 所在的宫
    int val = inout[i]; // 获得第i个元素的值
    rows[row][val] = true; // 表示在第row行中val已经被填了
    cols[col][val] = true; // 在第col列中val已经被填了 
    boxes[box][val] = true; // 在第box宫中val已经被填了 
  }

我们继续:

/* Dance结构的构造函数Dance */

// 下面的代码对于上面的算法做了改进,主要干的事情是,将那些已经填入了数字的列剔除了.
// 这样的话,可以加快程序的执行速度.
//
for (int i = 0; i < N; ++i) { // 初始化第1~81列
    if (inout[i] == 0) { // 第i格需要填写,将不需要填写的列剔除掉
      append_column(i);
    }
}

// 一共是9行,9列,对于每一行,应该是能够填写9个元素的,但是实际上,可以做一些裁剪
// 那些不能填入的数字对应的列一律剔除
for (int i = 0; i < 9; ++i) { 
    for (int v = 1; v < 10; ++v) {
      if (!rows[i][v]) // 如果rows[i][v]==0,表示第i行可以填入v 
        append_column(get_row_col(i, v));
      if (!cols[i][v]) // 如果cols[i][v]==0,表示第i列可以填入v
        append_column(get_col_col(i, v));
      if (!boxes[i][v]) // 如果boxes[i][v]==0,表示第i宫可以填入v
        append_column(get_box_col(i, v));
    }
}

看一下append_column是如何定义的吧:

void append_column(int n)
{
    Column* c = new_column(n); 
    put_left(root_, c); // 将c添加到root_所在的行
    columns_[n] = c; // 记录下表头
}

void put_left(Column* old, Column* nnew) // 将nnew放在old的左边
{
    // 这里需要特别注意的一点是,一般而言,old代表了一个双向链表
    nnew->left = old->left;
    nnew->right = old;
    old->left->right = nnew;
    old->left = nnew;
}

// 下面的函数主要实现从逻辑下标到实际下标的映射

int get_row_col(int row, int val) // 得到第row行的val对应的下标,这里实际上实现了一个映射函数 
{
  // kRow=100,这里需要注意,并不是81,这里是为了简单,如果你想极力
  // 减少内存占用,可以考虑将kRow从100变为81,毕竟数组下标从81~99都是空闲的
    return kRow + row * 10 + val; 
}

int get_col_col(int col, int val) // 得到第col列的val所在的下标
{
    return kCol + col * 10 + val;
}

int get_box_col(int box, int val) //  得到第box宫的val所在的下标
{
    return kBox + box * 10 + val;
}

我们继续来分析Dance的构造函数:

/* Dance结构的构造函数Dance */

// 下面的代码片段开始构建行了,上面的主要是构建交叉十字循环双向链的头部部分
// 下面的话,开始构建链表的`体`了
for (int i = 0; i < N; ++i) {
    if (inout[i] == 0) {
      int row = i / 9;
      int col = i % 9;
      int box = row / 3 * 3 + col / 3;
      
      for (int v = 1; v < 10; ++v) {
        if (!(rows[row][v] || cols[col][v] || boxes[box][v])) { 
          // 第row行,第col列,第box宫都可以填入v (这个条件必须满足)
          Node* n0 = new_row(i);
          Node* nr = new_row(get_row_col(row, v));
          Node* nc = new_row(get_col_col(col, v));
          Node* nb = new_row(get_box_col(box, v));
          // 这里的4个Node对应上面的四个约束条件
          // 这里实际上说明了,一旦在n0,nr,nc,nb中任意一个填入了数v,那么其余的都不能填v了. 
          // nr代表该元素所在的行,nb表示所在的宫,nc代表所在的列
          // n0,nr,nc,nb实际上成为了一行,同时双向链表除了标头那一行外,每一行都只有4个元素,不多不少
          put_left(n0, nr); // 将nc, nr, nb加入n0所在的行
          put_left(n0, nc);
          put_left(n0, nb);
        }
      }
    }
}

关于new_row函数:

Node* new_row(int col) // 构建新行
{
    Node* r = &nodes_[cur_node_++]; // 分配空间 
    memset(r, 0, sizeof(Node));

    r->left = r;
    r->right = r;
    r->up = r;
    r->down = r;
    r->name = col;  // col记录了表头所在的元素在columns_数组中的下标
    r->col = columns_[col]; // 指向表头 
    put_up(r->col, r); // 将r加入r->col所在的列
    return r;
}

void put_up(Column* old, Node* nnew) // 将nnew放在old的上面
{
   // 如果old是表头元素,那么nnew就是插入到该列的尾部
   // 不过,说实话,nnew在old所在的列的哪个位置并不重要,因为我们并不需要nnew的确切位置
   // 只要保证nnew在这一列即可 
    nnew->up = old->up; // 需要注意的是,Column结构是一个十字交叉链表
    nnew->down = old;
    old->up->down = nnew;
    old->up = nnew;
    old->size++; // size表示这一列增加了一个元素
    nnew->col = old; // 表头 
}

上面部分的代码,完成了数独问题到解精确覆盖问题的转换,我在这里稍微来理一理:

精确覆盖问题要求解的是,给定一个由0-1组成的矩阵，是否能找到一个行的集合，使得集合中每一列都恰好包含一个1.

而这里的数独问题,我们看得到的,也转化成为了相同的一个问题:

对于0~80列(由于剔除了一些元素,可能没有那么多),这些列恰好包含一个1代表列对应的格子必须填入值.

对于100~199列(由于剔除了一些元素,可能没有那么多),这些列恰好包含一个1代表这些列对应到棋盘上的行必须填入对应的val.

对于200~299列(由于剔除了一些元素,可能没有那么多),这些列恰好包含一个1代表这些列对应到棋盘上的列必须填入对应的val.

对于300~399列(由于剔除了一些元素,可能没有那么多),这些列恰好包含一个1代表这些列对应到棋盘上的宫必须填入对应的val.

而这恰好对应前面算法中的四个约束条件.

这样构建出来的交叉十字循环双向链表,如果选择了某一行,就代表我们在棋盘上对应的格子a上填入了一个数字,这个数字填写了之后,会导致我们不能再选择a对应的列上其它元素所在的行了(每一列只能有1个1).因此要对双向链表进行裁剪.

初始化完成之后,我们就可以正式求解了:

bool solve_sudoku_dancing_links(int unused)
{
    Dance d(board);
    return d.solve();
}

继续来看solve函数,solve函数是使用递归进行求解:

bool solve() 
{
  if (root_->left == root_) { // 运行到了这里表示所有的列都被覆盖到了
    for (size_t i = 0; i < stack_.size(); ++i) {
      Node* n = stack_[i]; // 取出Node
      int cell = -1;
      int val = -1;
      while (cell == -1 || val == -1) {
        // 回忆前面的,在同一行的只有四个元素,n0, nr, nc, nb,通过遍历这四个元素,我们可以知道该怎么来填
        // n0中记录的下标(name域)是我们要填入的数据在inout_中的下标(小于100).
        // 而nr, nc, nb,我们任取其中一个,就可以知道在inout_[cell]中填入什么数据了
        if (n->name < 100) 
          cell = n->name;
        else 
          val = n->name % 10;
        n = n->right; 
      }
      inout_[cell] = val;
    }
    return true;
  }

  Column* const col = get_min_column(); // 获得元素最少的列,这样可以减少计算量
  cover(col);
  for (Node* row = col->down; row != col; row = row->down) { // 一个回溯的过程
    stack_.push_back(row);
    for (Node* j = row->right; j != row; j = j->right) { // 将row所在行的数据全部删除
      cover(j->col);
    }
    if (solve()) { // 将问题的规模缩小,递归可解
      return true;
    }
    stack_.pop_back(); // 运行到了这里说明上面的solve()失败,因此要恢复现场
    for (Node* j = row->left; j != row; j = j->left) {
      uncover(j->col);
    }
  }
  uncover(col); 
  return false;
}

回头看一下cover函数:

void cover(Column* c) // 所谓的cover,表示我们选择了这一列,我们就要将这一列中其它元素所在的行移除
{
  c->right->left = c->left;
  c->left->right = c->right; // 在表头这一行中删除掉c 
  for (Node* row = c->down; row != c; row = row->down) { // 遍历c所在列的元素
    for (Node* j = row->right; j != row; j = j->right) { // 解除该元素所在行
      j->down->up = j->up;
      j->up->down = j->down;
      j->col->size--;
    }
  }
}

以及uncover函数:

void uncover(Column* c) // 上面函数的逆函数
{
  for (Node* row = c->up; row != c; row = row->up) {
    for (Node* j = row->left; j != row; j = j->left) {
      j->col->size++;
      j->down->up = j;
      j->up->down = j;
    }
  }
  c->right->left = c;
  c->left->right = c;
}

这样的话,函数就完成了.

完整的代码

#include 
#include 
#include