第一周
介绍
这是啥?
这是一个由希伯来大学的 Shimon Schocken与 Noam Nisan讲授的课程。
教你从最简单的与非门实现计算机,并在计算机上实现操作系统,最后在构建的计算机上完成俄罗斯方块的制作。
官网主页:http://www.nand2tetris.org
Coursera课程主页:https://www.coursera.org/learn/build-a-computer
我将它的视频课程搬运到了B站,方便大家学习:https://space.bilibili.com/69824765/#/channel/detail?cid=56426
如果能科学上网的话,也可以在youtube搜索Nand2Tetris。
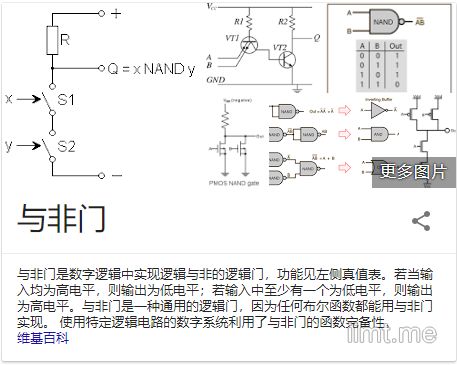
什么是Nand2Tetris
Nand就是与非门电路:
Tetris就是俄罗斯方块。
我们知道计算机就是由各种门电路组成的,所以作者的这个课程就是从最基础的与非门电路开始,构建一个计算机,在计算机上实现操作系统,然后在操作系统中玩俄罗斯方块。是不是很有意思?
开始
开始之前,要做点准备工作:
1. 下载初始代码与测试工具
2. 下载JDK
作者给我们提供了一个硬件模拟工具,我们通过编辑.hdl文件来描述一个门电路的逻辑,然后使用测试工具就可以测试我们设计的门电路是否正确。由于测试工具是基于Java的,需要下载安装JDk,怎么安装请自行百度。
初始代码与测试工具都在这里下载:https://www.nand2tetris.org/software
第一周01
其实第一周应该是00,但是00其实是作者为了让学者熟悉环境用的,所以我就跳过了。
.hdl文件
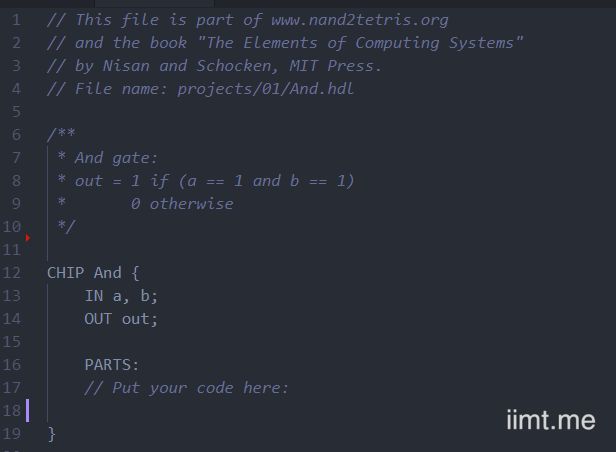
这个项目中,门电路是由.hdl文件来实现的,就是下面这样:
在中间的注释部分,告诉了你这个门的输入输出的关系,你需要完成PARTS。
下面的IN就是输入端,OUT就是输出端。PARTS中写上如何将信号a与b输出即可(具体怎么写继续看下去)。
目标
这一周主要是完成四个门电路,以及他们的多位复合电路:
1. Not 非门
2. And 与门
3. Or 或门
4. Xor 异或门
5. Mux 多路选择器/多路开关
6. DMux 数据分配器
7. And16 16位的与门
8. DMux4Way 4通道的数据分配器
9. DMux8Way 8通道的数据分配器
10. Mux16 16位多路选择器
11. Mux4Way16 4通道的16位多路选择器
12. Mux8Way16 8通道的16位多路选择器
13. Not16 16位的非门
14. Or16 16位的或门
15. Or8Way 8通道的或门
1. Not - 非门
我们现在只有一个门,就是Nand门,看一下这个东西的真值表:
| a | b | out |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
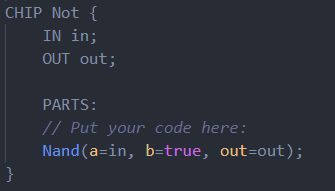
观察第二行与第四行,b为1的时候,out总是等于非a。
所以就这样实现非门了:
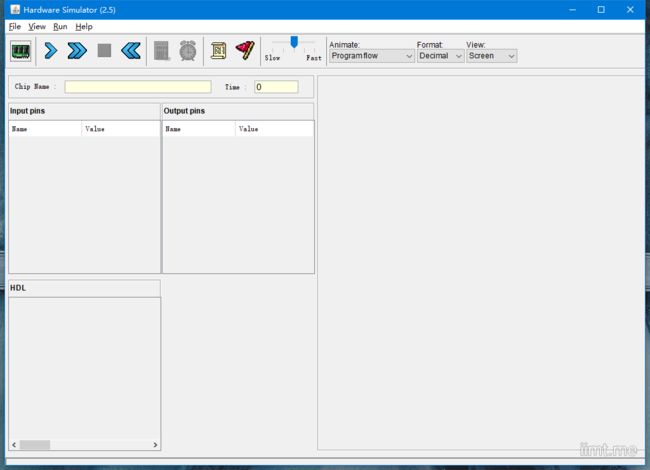
然后来测试一下,打开Tools文件夹下的 HardwareSimulator.bat (macOS下打开HardwareSimulator.sh, 如果打开不了检查java环境是否配好)
点击红色旗子旁边的脚本按钮,选择 nand2tetris > 01 > Not.tst,然后按左边的第三个前进按钮
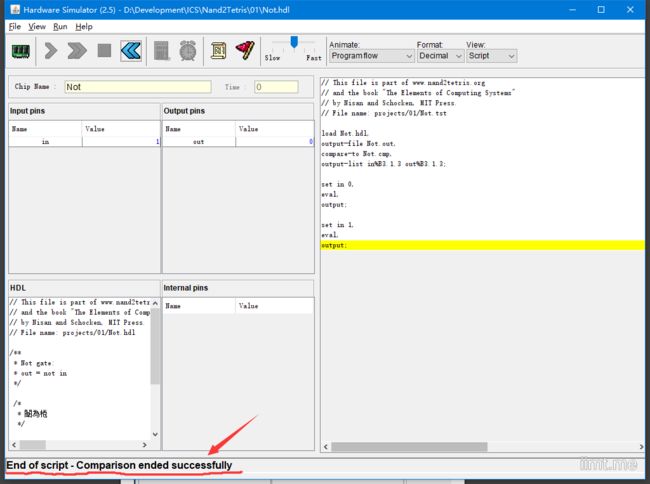
然后脚本就会自动导入你写的Not.hdl,然后测试这个门到底正不正确,如果输入1输出也是1的话,肯定就会错了。如果没有问题,就会一直跑完,这样:
这样就完成了一个门,然后我们现在有两个门了,Nand与非门与Not非门,再用这两个门来完成其他的门电路。
其他And、Or这几个门就不多说了自己做吧,直接来说Mux。
Mux 多路选择器
这个门有三个输入,a,b,sel。
当sel = false时,输出a,当sel=true时输出b。
这里我们可以自己想出一个公式,至于公式怎么出来的,可以百度一下卡诺图化简。
out = Or(
And(
Not(sel), a
),
And(
sel, a
)
)
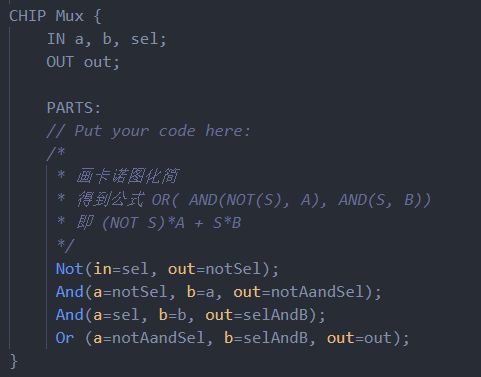
所以最后实现Mux:
基础门
基础门这里就详细写两个,其他的And,Or,Dmux都自己想办法通过已经实现的门来实现吧。如果遇到问题,可以在百度搜索卡诺图化简通过真值表化简出公式,再不济就去github上面搜索Nand2Tetris,看看别人都是怎么实现的。
复合多路门我这里也只详细介绍And16与DMux4Way,参考这两个实现其他的就好。
And16
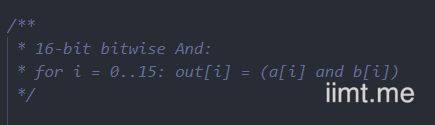
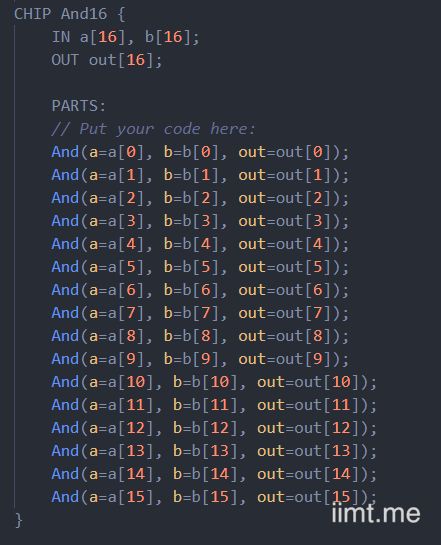
在And16.hdl中,它是这样描述的:
即: out[i] = And(a[i], b[i])
所以每个都写一遍出来就好了,不要想循环啊啥的,现在你手头只有Nand,And,Not,Or这几个门电路,所以只能手写。
最后实现方案:
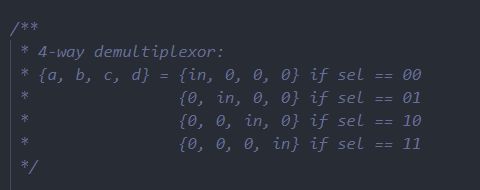
DMux4Way
看看介绍:
前面已经实现了DMux,当sel=0时输出{in, 0},sel=1时输出{0, in}。也就是说是sel来决定in在左边还是在右边。
在4Way中,可以看作两次选择:
PS: 在.hdl中,如果sel = 01,则sel[1] = 0,sel[0] = 1,也就是倒序的。
sel[1]决定in出现在前两个还是后两个的位置中。
sel[0]决定in出现在两个中的前一个还是后一个位置。
我们把输出{a, b, c, d}分成两部分{a, b}和{c, d},
先根据sel[1]将这两部分的元素都置为相同的in或0
DMux(in=in, sel=sel[1], a=left1, b=right1); ①
DMux(in=in, sel=sel[1], a=left2, b=right2); ②
这样的结果将会是{0, 0, in, in}或{in, in, 0, 0}
left1和left2肯定是相同的,right1和right2肯定是相同的。
然后根据sel[0]将前两个和后两个部分设置出来,:
DMux(in=left1, sel=sel[0], a=a, b=b);
DMux(in=right1, sel=sel[0], a=c, b=d);
OK
基础门和复合门都可以参照这几个有代表性的来做,写完之后使用工具测试一下写的对不对,测试都通过,这一周的门电路就算全部完成了。
结语
这一周实现的这些基础电路后面会再次封装,变成功能更强大的工具。