科学是人们敬崇的名词,那么科学的本质是什么呢?科学的本质是事物要素见得关联关系:1.圆周率是几何中圆的周长和直径的比叫做圆周率,通常用希腊字母π表示,圆周率是一个无限不循环小数,即为无理数,他的前十位小数位:π=3.1415926535…。我国古代的数学家对圆周率的研究有过很大贡献,其中以祖冲之的贡献最为突出,他算得π的值在3.1415926和3.1415927之间。并用22/7 和355/113 作为圆周率搞得近似值。2.黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。其比值是一个无理数,用分数表示为(√5-1)/2,取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。
这个分割点就叫做黄金分割点(golden section ratio),通常用Φ表示。这是一个十分有趣的数字,以0.618来近似表示,通过简单的计算就可以发现:(1-0.618)/0.618≈0.618,即一条线段上有两个黄金分割点。
计算公式:
向左转|向右转
向左转|向右转
扩展资料
黄金分割点美学价值:
因为它在造型艺术中具有美学价值,在工艺美术和日用品的长宽设计中,采用这一比值能够引起人们的美感,在实际生活中的应用也非常广泛,建筑物中某些线段的比就科学采用了黄金分割,舞台上的报幕员并不是站在舞台的正中央,而是偏在台上一侧,以站在舞台长度的黄金分割点的位置最美观,声音传播的最好。
就连植物界也有采用黄金分割的地方,如果从一棵嫩枝的顶端向下看,就会看到叶子是按照黄金分割的规律排列着的。在很多科学实验中,选取方案常用一种0.618法,即优选法,它可以使我们合理地安排较少的试验次数找到合理的西方和合适的工艺条件。
正因为它在建筑、文艺、工农业生产和科学实验中有着广泛而重要的应用,所以人们才珍贵地称它为"黄金分割"。黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值。应用时一般取0.618 ,就像圆周率在应用时取3.14一样。
并且人们认为如果符合这一比例的话,就会显得更美、更好看、更协调。在生活中,对“黄金分割”有着很多的应用。如:最完美的人体:肚脐到脚底的距离/头顶到脚底的距离=0.618;最漂亮的脸庞:眉毛到脖子的距离/头顶到脖子的距离=0.618。
黄金分割律,又名黄金率,即把已知线段分成两部分,使其中一部分对于全部的比等于其余一部分对于这部分的比。最基本的公式就是把1分割成0.618与0.382,尔后再依据实际情况变化,再演变成其他的计算公式。
黄金分割律是公元前六世纪,希腊的大数学家毕达哥拉斯发现的。它的基本内容可以这样解释:如果把一条线段分成两部分,长段和短段的长度之比是1:0.618,整条线段和长段的比也是1:0.618时,才是和黄金一样最完美的分割,进行分割的这个点就叫黄金分割点。
计算公式(5^0.5-1)/2=(2.236-1)/2=0.618
等的两部分是教程部分为原来线段和较短部分的比例中项呢?
这个就是我们在初中相似三角形中,所接触到的一个叫做黄金分割问题。今天小编想讲的是如何把一个线段进行黄金分割呢?下面小编在此分享一个方法给大家。
首先我们需要准备的工具是:圆规、直尺、铅笔和橡皮擦。这些工具准备好了之后,我们来按照下面的步骤,把一个线段进行黄金分割。
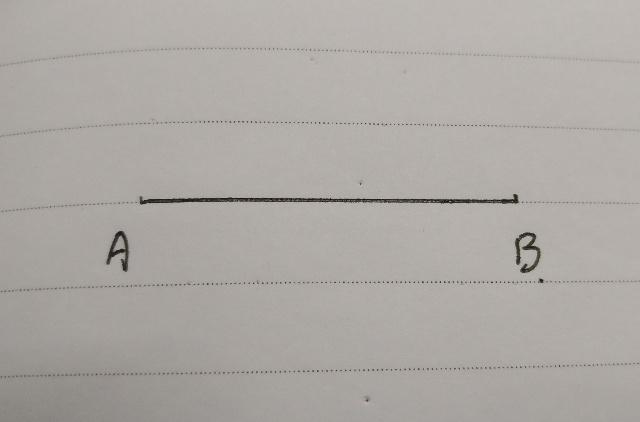
第一步:画一条线段AB,如下图所示:
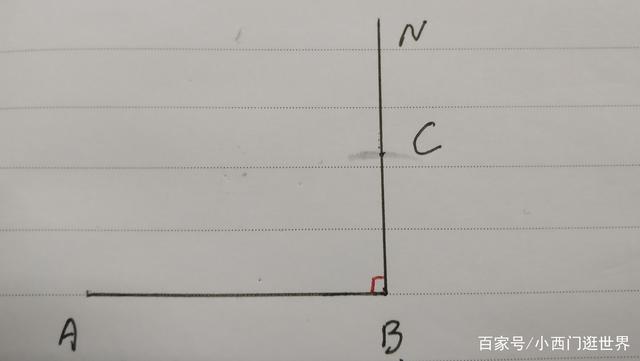
第二步:过B点作AB的垂线BN,并且在垂线BN上用圆规截取BC=1/2AB,如下图所示:
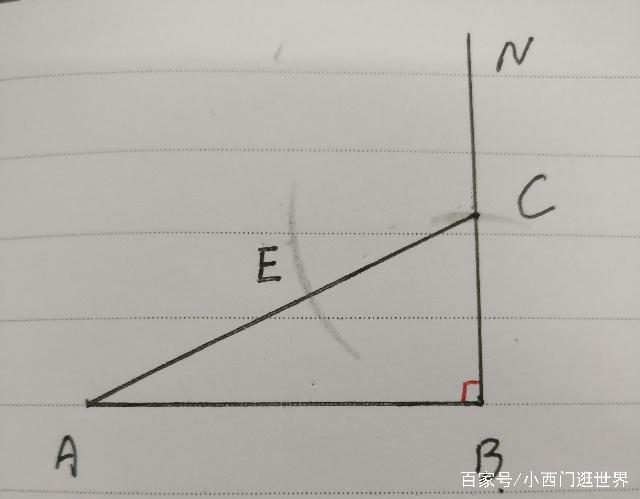
第三步:连接AC,以点C为圆心,BC长为半径画弧,交AE于点E,如下图所示:
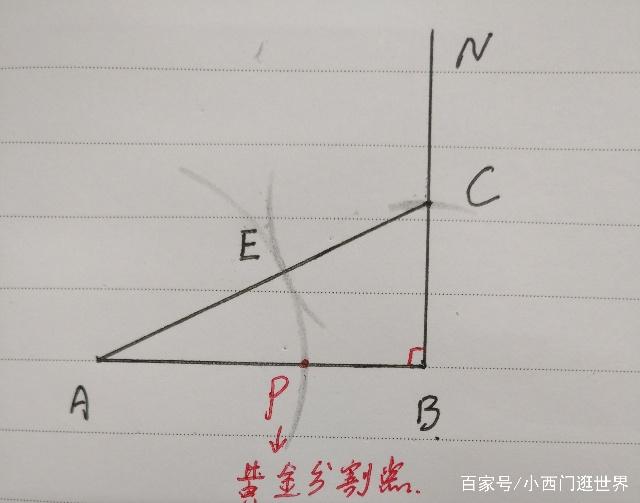
第四步:再以A为圆心,AE长为半径画弧,交AB于点P,此时的P点就是我们所要求的黄金分割点,如下图所示:
那么我们如何来说明我们所做的图是正确的呢?下面小编就给出证明的方法,如图所示:
我们也可以利用这个一元二次方程,他解出来这个比值的近似值为0.618,对于这个比值我们称之为黄金数。
0.618这个近似值在几何作图上有很多应用。比如说,如果我们要想画一个举行他的宽与长得比,也是近似于0.618,那我们就说这个矩形就是黄金矩形,如下图:
再比如我们画的五角星,它的各边也是按照黄金分割进行划分的。
黄金分割也经常被广泛运用在建筑设计,美术,音乐,艺术等方面。
比如我们家的门窗,它们的宽和长得比也经常设计为近似0.618,因为这样可以引起美感。
3.直角三角形的边角关系,也就是直角三角形要素间的关联关系:三边之间的关系a²+b²=c²(勾股定理)
锐角之间的关系∠A+∠B=90°
边角之间的关系sinA=a/ccosA=b/ctanA=a/b
能够正确认识事物就要认清要素间的关联关系,因为科学的本质是事物要素间的关联关系。
待续…: