质因数分解的复杂是公认,这也是我们将他作为 RSA (一种广泛使用的公钥加密算法)的数学难题的原因。
\(N=P*Q\) (P、Q是质数),n = length of N in bit
对于这么一个N,我们因数分解得到结果的时间复杂度是 \(2^n\) ,因为这个复杂,所以也有一堆的数学家在努力降低这个的时间复杂度,目前的优化结果的时间复杂度是 \(2^{ \sqrt[3]{n}}\) 。
那么量子是否能够有更好的结果呢?
在讲因数分解之前,需要先提周期查找算法。
周期查找 Period Finding
周期查找的基础是 量子傅里叶变换 。
Input :
\(f:(0,1,2,…,M-1) \rightarrow S\) for all x \(f(x)=f(x+r)\)
challenge :
find r
condition:
1) f is 1-1 on period 在周期内,f是一个一一对应的函数
2)\(M>>r\) \(M>2r^2\)
3)M能够被r整除 (这是一个简化条件,稍后会有不简化的怎么办)
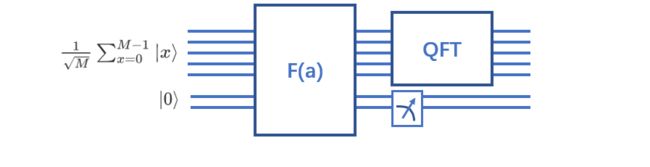
这个电路,我的输入是 $ \frac{1}{\sqrt M} \sum_{x=0}^{M-1} |x\rangle |0\rangle$
经过f(x)后,我的量子叠加态是 $ \frac{1}{\sqrt M} \sum_{x=0}^{M-1} |x\rangle |f(x)\rangle$
此时,如果测量了下面的 f(x),那么上面的量子态会坍缩,会变成只有f(x)等于测量结果的x,显而易见,这是一个周期函数。
在 量子傅里叶变换 中,我们提到过傅里叶变换的第一个特点,当输入shift了,结果是不会变的。
如果我们输入的量子态的概率幅为 \(\alpha_0 , \alpha_1, \alpha_2, \alpha_3,…, \alpha_{N-1}\) ,输出的量子态的概率幅为 \(\beta_0 , \beta_1, \beta_2, \beta_3,…, \beta_{N-1}\)
则,当我们将输入的概率幅变为:\(\alpha_{N-},\alpha_0 , \alpha_1, \alpha_2, …, \alpha_{N-2}\) 输出的概率不变。(这里写得是概率,不是概率幅,概率是概率幅的平方)
也就是说,我测量的随机结果可能是这个周期当中的i个值,我也能shift成在第一个位置。
即,把 [0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 ……] (每个周期五个,第三个为1,其余为0) 变成 [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 …… ] (每个周期五个,第三个为1,其余为0) 。
他们经过傅里叶变换后的结果是一样的。
其实到这里,我们发现,我们测不测量f(x)其实都没有关系,因为在这前面所有测量结果对应的x,都是同一个周期的周期函数,因为shift的原因,他们傅里叶变换后的结果都是一样的。
那么,这么做的意义是?
量子傅里叶变换还有第二个特点:傅里叶变换可以改变周期函数的周期。

他可以把周期为r的函数,变成周期为 \(\frac{M}{r}\) 的函数。
对最后的这个函数测量,得到的结果是 \(\frac{M}{r}\) 的倍数,多测量几次就知道了 \(\frac{M}{r}\) 的值。知道了这个值,很容易反推出r的值,周期查找完成。
如果没有简化条件呢?
即,M不是r的倍数。
那,假设测量结果为L,则找到一个最接近 \(\frac{L}{M}\) 的分数 \(\frac{t}{r}\) ,唯一的要求是 \(M>2r^2\) 最后通过一种叫做continued fraction的方法找到r。
因数分解
一个例子:
问题:找N=21的因数。
解法:
step 1:
\(2^0=1 (\mod 21)\) 除以21后余数为1
\(2^1=2 (\mod 21)\)
\(2^2=4 (\mod 21)\)
\(2^3=8 (\mod 21)\)
\(2^4=16 (\mod 21)\)
\(2^5=11 (\mod 21)\)
\(2^6=1 (\mod 21)\)
step 2:
\(2^6-2^0=0 (\mod 21)\)
\(2^6-1=0 (\mod 21)\)
\((2^3-1)(2^3+1)=0 (\mod 21)\)
到这一步,我们发现了什么?
\((2^3-1)(2^3+1)\)是21的倍数,那么他的两个因数 \((2^3-1)\) 和 \((2^3+1)\) 一定和21有公约数。
gcd(21,7)=7
gcd(21,9)=3
gcd求最大公约数大家还熟悉吗?
比如说,我们相找21和15的最大公约数。
\(21=15*1+6\)
\(15=6*2+3\)
\(6=3*2+0\)
最大公约数就是最后一个不为0的余数,这里就是3。求最大公约数的算法很快,大概是在 \(log N\) 的级别。
那么现在的问题其实就是step1 ,找到函数 \(f(a)=x^a \mod N\) 的周期,在上述例子中 \(2^0\) 和 \(2^6\) 取余相等,这就是一个周期,周期为6.
现在因数分解问题就全部转化为了周期查找问题。
而周期查找问题恰好,有量子加速的方法,前文已经提过了,不再累述,我们知道周期查找有一个前提条件是 \(M> 2r^2\) ,在这个例子中,我们不知道r是多少,这个是我们要求的,但是我们知道,r
变成电路图就是:
得到周期,然后经过 step 2 就是我们想要的因数分解。
参考资料:
Quantume Mechanics & Quantume Computation Lecture 10
