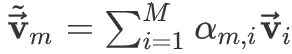一、简介
来自论文:《Attention is all you need》
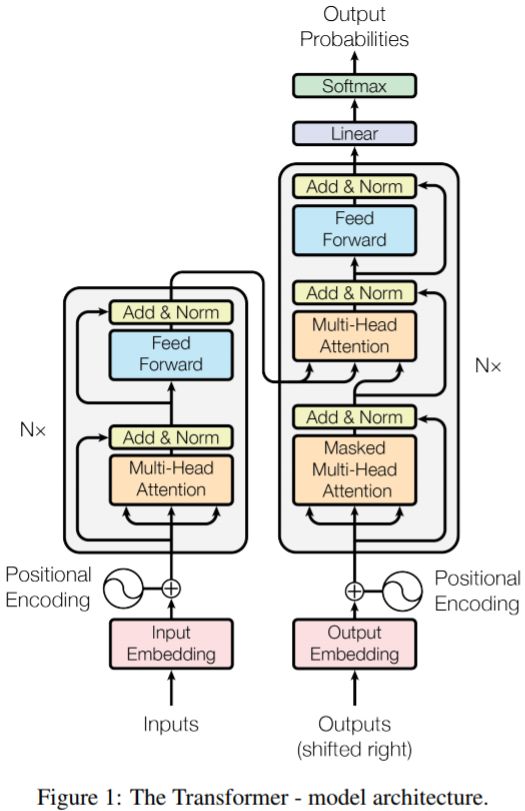
由google团队在2017年发表于NIPS,Transformer 是一种新的、基于 attention 机制来实现的特征提取器,可用于代替 CNN 和 RNN 来提取序列的特征。 在该论文中 Transformer 用于 encoder - decoder 架构。事实上 Transformer 可以单独应用于 encoder 或者单独应用于 decoder 。
Transformer相比较LSTM等循环神经网络模型的优点:
- 可以直接捕获序列中的长距离依赖关系;
- 模型并行度高,使得训练时间大幅度降低。
二、结构
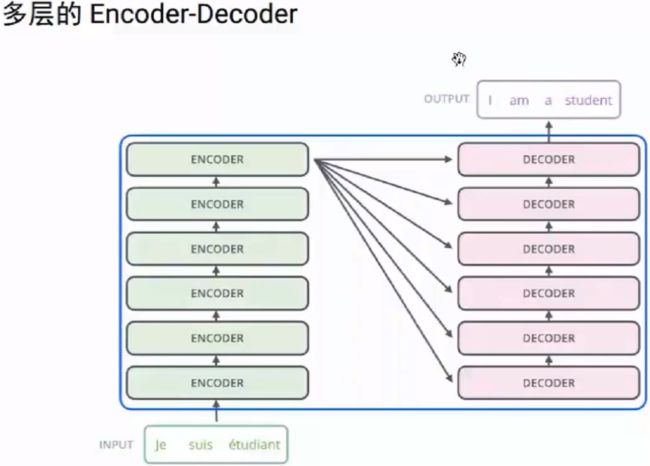
1.Transformer 包含一个编码器 encoder 和一个解码器 decoder 。
2.编码器 encoder 包含一组 6 个相同的层 Layer ,每层包含两个子层 SubLayer。
(1)第一个子层是一个多头自注意力multi-head self-attention层,第二个子层是一个简单的全连接层。
(2)每个子层都使用残差直连,并且残差直连之后跟随一个layer normalization:LN;假设子层的输入为h,则经过LN之后整体的输出为:LayerNorm(h+Sublayer(h));为了Add直连,论文将内部所有层的输入、输出的向量维度设置为$d_{model}=512$维。
3.解码器decoder也包含一组6个相同的层Layer,但是每层包含三个子层SubLayer。
(1)第一个子层也是一个多头自注意力multi-head self-attention层,但是,在计算位置i的self-attention时屏蔽掉了位置i之后的序列值,这意味着:位置i的attention只能依赖于它之前的结果,不能依赖它之后的结果。因此,这种self-attention也被称作masked self-attention。
(2)第二个子层是一个多头注意力multi-head attention层,用于捕获decoder output和encoder output之间的attention。第三个子层是一个简单的全连接层。
(3)和encoder一样:每个子层都使用残差直连,并且残差直连之后跟随一个layer normalization:LN;decoder所有层的输入、输出的向量维度也是$d_{model}=512$维。
(1)Encoder
self-Attenention计算每个x1时候,依赖其他所有的x,FNN不依赖其他的x
(2)Decoder
1.self-attention
1.1 self-Attention计算
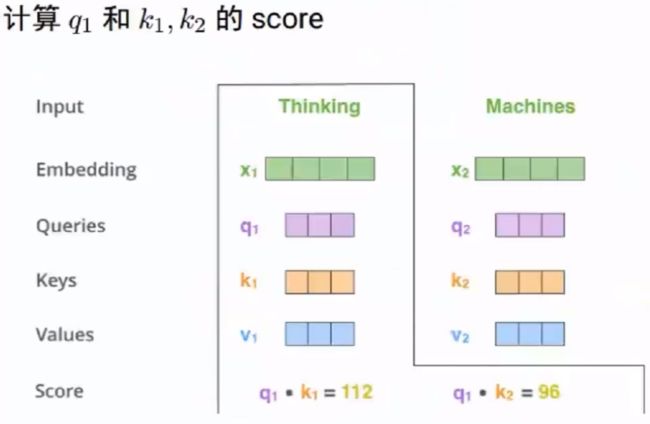
把每个词变换成三个向量Q、K和V
q1:表示为了编码x1,用来查询别人的向量
k1:表示被别人查询的向量
v1:表示该词真正的语义向量
普通Attention:
query是decoder的隐状态;
key是encoder的输出;
value是encoder的输出
普通Attention是self-attention的特例
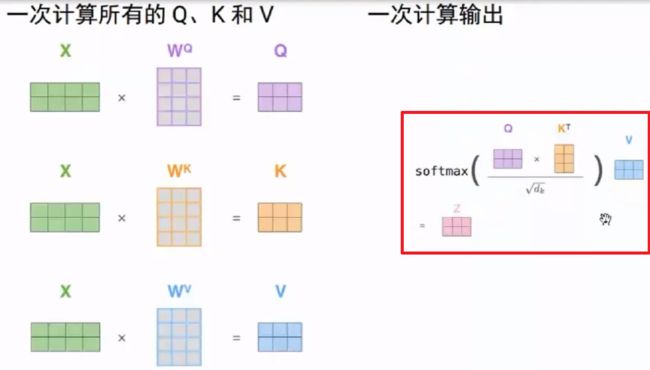
为什么要除以根号d:为了降低Q*K的数值,防止它落入到softmax函数的饱和区间。因为softmax函数的饱和区梯度几乎为0,容易发生梯度消失。
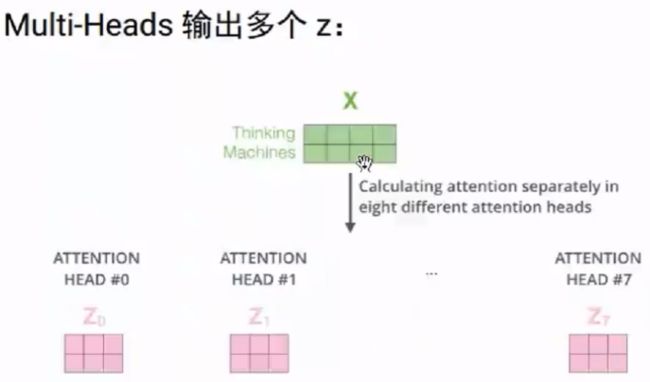
1.2 Multi-Heads attention
(1)多头attention将整个attention空间拆分成多个attention子空间(一个指代消解、一个上下位,...),其表达能力更强。从原理上看,multi-head相当于在整体计算代价几乎保持不变的条件下,引入了更多的非线性从而增强了 模型的表达能力。
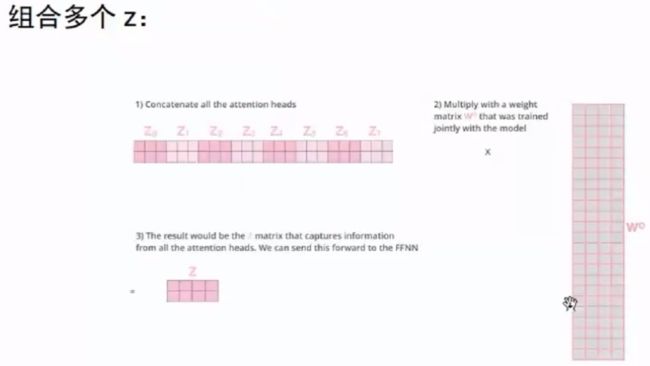
(2)多头注意力机制的三种实现方式:
encoder-decoder attention:query 来自前一个 decoder 层的输出,keys,values 来自 encoder 的输出。 其意义是: decoder 的每个位置去查询它与 encoder 的哪些位置相关,并用 encoder 的这些位置的 value 来表示。
encoder self-attention:query,key,value 都来自前一层 encoder 的输出。 这允许 encoder 的每个位置关注 encoder 前一层的所有位置。
decoder masked self-attention:query,key,value 都来自前一层 decoder 的输出。 这允许 decoder 的每个位置关注 encoder 前一层的、在该位置之前的所有位置。
2.全连接层
encoder 和 decoder 还包含有全连接层。对 encoder/decoder 的每个 attention 输出,全连接层通过一个 ReLU 激活函数以及一个线性映射:$o_m=W_2 max(0,W_1v_m+b_1)+b_2$
对于同一个 multi-head attention 的所有M个输出,采用相同的参数;对于不同的 multi-head attention 的输出,采用不同的参数。
输入和输出的维度保持为$d_{model}=512$ ,但是中间向量的维度是 2048 维 。这是为了扩充中间层的表示能力,从而抵抗 ReLU 带来的表达能力的下降。
3.embedding层
网络涉及三个 embedding 层:
encoder 输入 embedding 层:将 encoder 输入 token 转化为 维的向量。
decoder 输入 embedding 层:将 decoder 输入 token 转化为 维的向量。
decoder 输出 embedding 层:将 decoder 输出 token 转化为 维的向量。
在论文中这三个 embedding 矩阵是共享的,并且论文中在 embedding 层将该矩阵乘以一个常量$\sqrt{d_{model}}$ 来放大每个权重。
4.position embedding
(1)从 attention 的计算公式可以看到
调整输入的顺序对 attention 的结果没有任何影响。即:attention 的输出中不包含任何顺序信息。 事实上输入的顺序对于很多任务是非常重要的,比如 北京到上海的机票 与 上海到北京的机票 的语义完全不同。
(2)论文通过将位置编码添加到 encoder 和 decoder 底部的输入 embedding 来解决问题。即有:
其中$p_i$为位置i的position embedding,$\alpha_{m,i}^p$ attention权重与位置有关。对于同一个输入序列如果打乱序列顺序,则不同token的attention权重发生改变使得attention的结果不同。
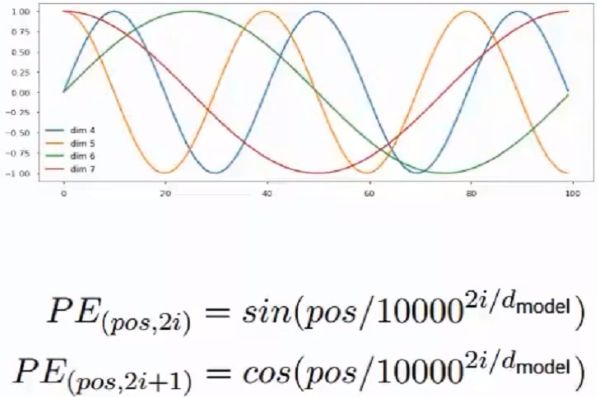
(3)位置编码有两种选择:
- 可以作为参数来学习,即:将encoder的每个输入的位置embedding、decoder的每个输入的位置embedding作为网络的参数,这些参数都从训练中学得;缺点:对于下面的例子,两个北京和上海的位置编码不同,例:北京到上海的机票 VS 你好,我要北京到上海的机票
- 也可以人工设定固定值
论文的实验表明:通过参数学习的position embedding 的效果和采用固定的position embedding 相差无几。 另外,固定方式的 position embedding 可以在测试阶段处理那些超过训练序列长度的测试序列。
三、Tips
1.使用multi-head attention的三个适用场景:
encoder-decoder attention:使用multi-head attention,输入为encoder的输出和decoder的self-attention输出,其中encoder的self-attention作为 key and value,decoder的self-attention作为query
encoder self-attention:使用 multi-head attention,输入的Q、K、V都是一样的(input embedding and positional embedding)
decoder self-attention:在decoder的self-attention层中,deocder 都能够访问当前位置前面的位置
2.位置编码
见第二章第4节
3.残差
每个encoder里面的每个sub-layer,都有残差连接,可以回传梯度
4.Layer Norm
每个sub-layer后面还有一步layer-normalization,可以加快模型收敛速度。
5.decoder的masked self-attention
注意encoder里面是叫self-attention,decoder里面是叫masked self-attention。
这里的masked就是要在做language modelling(或者像翻译)的时候,不给模型看到未来的信息。
6.优化
四、Transformer vs CNN vs RNN
1.假设输入序列长度为n,每个元素的维度为$d:\{x_1,...,x_n\}$,输出序列长度也为n,每个元素的维度也是d:$\{y_1,...,y_n\}$,从每层的计算复杂度、并行的操作数量、学习距离长度三个方面比较Transformer、CNN、RNN三个特征提取器:
1.每层的计算复杂度:
考虑到n个key和n个query两两点乘,因此self-attention每层计算复杂度为$O(n^2*d)$
考虑到矩阵(维度为$n*n$)和输入向量相乘,因此RNN每层计算复杂度为$O(n*d^2)$
对于k个卷积核经过n次一维卷积,因此CNN每层计算复杂度为$O(k*n*d^2)$,如果考虑深度可分离卷积,则计算复杂度下降为$O(k*n*d+n*d^2)$
因此:
当$n 当$n>d$时,可以使用受限self attention,即:计算attention时仅考虑每个输出位置附近窗口的r个输入。这将带来两个效果:每层计算复杂度降为$O(r*n*d)$ 最长学习距离降低为r,因此需要执行$O(n/r)$次才能覆盖到所有输入。 可以通过必须串行的操作数量来描述: 对于self-attention,CNN,其串行操作数量为O(1),并行度最大; 对于RNN,其串行操作数量为O(n),较难并行化。 覆盖所有输入的操作的数量 对于self-attention,最长计算路径为O(1);对于self-attention stricted,最长计算路径为O(n/r); 对于常规卷积,则需要O(n/k)个卷积才能覆盖所有的输入;对于空洞卷积,则需要$O(log_kn)$才能覆盖所有的输入; 对于RNN,最长计算路径为O(n) 通过检查模型中的注意力分布,可以展示与句子语法和语义结构相关的信息。 参考文献: 【1】BERT专题系列(二):Transformer (Attention is all you need)_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili 【2】NLP学习(5)----attention/ self-attention/ seq2seq/ transformer - Lee_yl - 博客园2.并行操作数量:
3.最长计算路径:
4.作为额外收益,self-attention可以产生可解释性的模型: