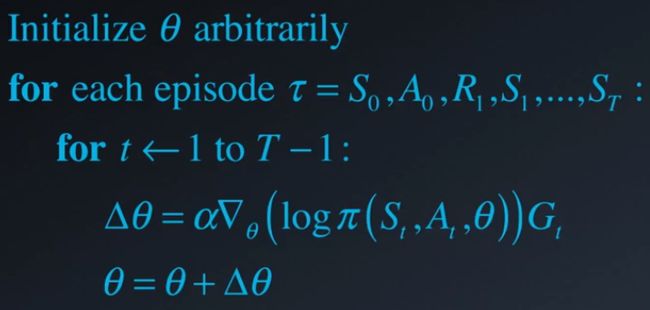Policy-Based methods
在上篇文章中介绍的Deep Q-Learning算法属于基于价值(Value-Based)的方法,即估计最优的action-value function $q_*(s,a)$,再从$q_*(s,a)$中导出最优的策略$\pi_*$(e.g., $\epsilon$-greedy)。但是有没有方法能不经过中间过程,直接对最优策略进行估计呢?这样做又有什么好处呢?该部分要介绍的就是这类方法,即基于策略(Policy-Based)的方法。下面先介绍一下这类方法的好处:
- 能够处理连续的动作空间(continuous action space)。在上篇文章中可以看出Value-Based方法适合离散有限的动作空间,但对于连续的动作空间就不能很好地处理。
- 能够得到最优的随机策略(stochastic policy)。尽管$\epsilon$-greedy等方式为策略选择加入了一定的随机性,但本质上Value-Based方法得到的最优策略是确定的,即对于同一状态$s$,对应同一动作$a$。举两个例子说明随机策略相对于确定策略的优势:
- 假设训练智能体玩石头、剪刀、布的游戏,最终的最优策略就是一个完全随机的策略,不存在确定的最优策略,因为任何固定的套路都可能会被对手发现并加以利用。
- 在和环境的交互过程中智能体常常会遇到同一种状态(aliased states),若对遇到的同一种状态都采用固定的动作有可能得不到最优的结果,特别是当智能体处在一个只能部分感知的环境(partially observable environment)中时。如下图所示,假设智能体的目标是吃到香蕉并且不吃到辣椒,但是它只能感知到与它相邻的格点的状况,在两个灰色的格点时智能体感知到的状况(即state)是相同的。假设智能体学习到的确定策略如箭头所示,则若智能体位置在黄框范围内时会出现来回地震荡,这显然不是最优的情况。
问题定义
假设策略$\pi$满足概率分布$\pi(s, a, {\theta})$,参数$\theta$控制着分布的形态,是需要进行优化的参数。首先定义目标函数$$J(\theta)=E_{\pi}[R(\tau)]\text{, }\tau=S_0,A_0,R_1,S_1,\cdots$$其中$R(\tau)$为score function, 用于评价策略的好坏,根据$R(\tau)$的不同形式可以有不同的目标函数,例如:$$\text{Average Action Value }J_{\bar{q}}(\theta)=E_{\pi}[q(s,a)]=\int_{s} \int_{a} \pi(s, a, {\theta}) q(s, a)dads$$
Policy Gradient
使用梯度上升的方式对参数进行求解: $\theta\leftarrow\theta+\alpha \nabla_{\theta}J(\theta)$,目标函数的梯度$\nabla_{\theta}J(\theta)$可写为如下形式:$$\nabla_{\theta}J(\theta)=\nabla_{\theta}E_{\pi}[R(\tau)]=E_{\pi}[\nabla_{\theta}(\log{\pi(s, a, {\theta})})R(\tau)]$$一种常用的计算方式是采用Monte Carlo方法对梯度进行估计:
下面举一个例子来进行说明,该例使用的是OpenAI的gym环境CartPole-v0,具体代码如下:
import tensorflow as tf import numpy as np import gym ### Create ENVIRONMENT env = gym.make('CartPole-v0') env = env.unwrapped env.seed(1) # Policy gradient has high variance, seed for reproducability ### ENVIRONMENT Hyperparameters state_size = 4 action_size = env.action_space.n ### TRAINING Hyperparameters max_episodes = 300 learning_rate = 0.01 gamma = 0.95 # Discount rate ### 计算一个episode中每个时间步的Gt并进行归一化处理 def discount_and_normalize_rewards(episode_rewards): discounted_episode_rewards = np.zeros_like(episode_rewards) cumulative = 0.0 for i in reversed(range(len(episode_rewards))): cumulative = cumulative * gamma + episode_rewards[i] discounted_episode_rewards[i] = cumulative # normalize mean = np.mean(discounted_episode_rewards) std = np.std(discounted_episode_rewards) discounted_episode_rewards = (discounted_episode_rewards - mean) / std return discounted_episode_rewards ### Create Policy Gradient Neural Network model tf.reset_default_graph() with tf.name_scope("PolicyNetwork"): input_ = tf.placeholder(tf.float32, [None, state_size], name="input_") actions = tf.placeholder(tf.int32, [None, action_size], name="actions") discounted_episode_rewards_ = tf.placeholder(tf.float32, [None,], name="discounted_episode_rewards") # Network Architechture fc1 = tf.contrib.layers.fully_connected(inputs = input_, num_outputs = 10, activation_fn=tf.nn.relu, \ weights_initializer=tf.contrib.layers.xavier_initializer()) fc2 = tf.contrib.layers.fully_connected(inputs = fc1, num_outputs = action_size, activation_fn=tf.nn.relu, \ weights_initializer=tf.contrib.layers.xavier_initializer()) fc3 = tf.contrib.layers.fully_connected(inputs = fc2, num_outputs = action_size, activation_fn=None, \ weights_initializer=tf.contrib.layers.xavier_initializer()) action_distribution = tf.nn.softmax(fc3, name='action_distribution') # Loss Function neg_log_prob = tf.nn.softmax_cross_entropy_with_logits_v2(logits = fc3, labels = actions) # -log(policy distribution) loss = tf.reduce_mean(neg_log_prob * discounted_episode_rewards_) # Optimizer train_opt = tf.train.AdamOptimizer(learning_rate).minimize(loss) ### Train the Agent allRewards = [] total_rewards = 0 maximumRewardRecorded = 0 episode = 0 episode_states, episode_actions, episode_rewards = [],[],[] saver = tf.train.Saver() #save model with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for episode in range(max_episodes): episode_rewards_sum = 0 state = env.reset() # Launch the game env.render() while True: # Choose action a from action distribution action_probability_distribution = sess.run(action_distribution, feed_dict={input_: state.reshape([1,4])}) action = np.random.choice(range(action_probability_distribution.shape[1]), p=action_probability_distribution.ravel()) # Perform action a new_state, reward, done, info = env.step(action) # Store s, a, r episode_states.append(state) action_ = np.zeros(action_size) action_[action] = 1 #one-hot encode for action episode_actions.append(action_) episode_rewards.append(reward) if done: ### Reward Info episode_rewards_sum = np.sum(episode_rewards) # Calculate sum reward for an episode allRewards.append(episode_rewards_sum) total_rewards = np.sum(allRewards) mean_reward = np.divide(total_rewards, episode+1) # Mean reward maximumRewardRecorded = np.amax(allRewards) print("==========================================") print("Episode: ", episode) print("Reward: ", episode_rewards_sum) print("Mean Reward", mean_reward) print("Max reward so far: ", maximumRewardRecorded) ### Calculate discounted accumulated reward Gt in each timestep discounted_episode_rewards = discount_and_normalize_rewards(episode_rewards) ### Feedforward, gradient and backpropagation loss_, _ = sess.run([loss, train_opt], feed_dict={input_: np.vstack(np.array(episode_states)), \ actions: np.vstack(np.array(episode_actions)), \ discounted_episode_rewards_: discounted_episode_rewards}) episode_states, episode_actions, episode_rewards = [],[],[] # clean episode info break state = new_state ### Save Model if episode % 100 == 0: saver.save(sess, "./models/model.ckpt") print("Model saved") ### Play the game using the trained agent with tf.Session() as sess: env.reset() rewards = [] saver.restore(sess, "./models/model.ckpt") # Load the model for episode in range(100): state = env.reset() step = 0 done = False total_rewards = 0 print("****************************************************") print("EPISODE ", episode) while True: ### Choose action a action_probability_distribution = sess.run(action_distribution, feed_dict={input_: state.reshape([1,4])}) action = np.random.choice(range(action_probability_distribution.shape[1]), p=action_probability_distribution.ravel()) new_state, reward, done, info = env.step(action) total_rewards += reward if done: rewards.append(total_rewards) print ("Score", total_rewards) break state = new_state env.close() print ("Score over time: " + str(sum(rewards)/len(rewards)))
Constrained Policy Gradient
参数$\theta$的更新可能会导致更新前后策略发生较大变化,使得训练过程不稳定,学习效率降低,因此考虑在目标函数中加入一个惩罚项(类似于机器学习中的正则项),防止策略的剧烈变化。$$J(\theta)=E_{\pi}[R(\tau)]-\beta D\left(\pi(\cdot, \cdot \theta), \pi\left(\cdot,\cdot,\theta^{\prime}\right)\right)$$其中$D$表示更新前后两种策略的变化,常用KL divergence来度量,即$$D\left(\pi(\cdot, \cdot \theta), \pi\left(\cdot,\cdot,\theta^{\prime}\right)\right)=D_{K L}\left(\pi\left(\cdot, \cdot, \theta^{\prime}\right) \| \pi(\cdot, \cdot, \theta)\right)=\int_s\int_a\pi(s, a, \theta^{\prime})\ln\frac{\pi(s, a, \theta^{\prime})}{\pi(s, a, \theta)}dads$$
Actor-Critic
基于策略的方法的难点在于如何评价策略的好坏,方法的主要缺点是收敛速度慢,训练花费时间长,并且容易收敛到局部最优值。例如在上一部分使用Monte Carlo进行计算的过程中由于不能直接计算action value $q(s,a)$,我们使用了$G_t$这个指标($G_t$、$q(s,a)$等概念的具体说明参考文章强化学习基础:基本概念和动态规划),因此需要等每个episode结束后才能开始更新$\theta$,并且$G_t$也不适用于continuing tasks。Actor-Critic结合了基于价值的方法和基于策略的方法,该方法通过Actor来计算并更新policy $\pi(s,a,\theta)$,通过Critic来计算并更新action value $\hat{q}(s,a,w)$:$$\text{Policy Update: }\Delta \theta=\alpha \nabla_{\theta}\left(\log \pi\left(S_{t}, A_{t}, \theta\right)\right) \hat{q}\left(S_{t}, A_{t}, w\right)$$
$$\text{Value Update: }\Delta {w}=\beta\left(R_{t+1}+\gamma \hat{q}\left(S_{t+1}, A_{t+1}, w\right)-\hat{q}\left(S_{t}, A_{t}, w\right)\right) \nabla_{w} \hat{q}\left(S_{t}, A_{t}, w\right)$$
Advantage Actor-Critic
在上篇文章介绍Deep Q-Learning算法的改进时提到了advantage value function $A(s,a)=Q(s,a)-V(s)$,这里使用该函数代替action value $Q(s,a)$,可以减少直接使用$Q(s,a)$带来的不稳定。$A(s,a)$的意义是用来度量在某个状态$s$下采取动作$a$相比在状态$s$的期望奖励额外多出的部分,若$A(s,a)>0$则参数朝着有利于该动作的方向更新,$A(s,a)<0$则朝着相反的方向更新。$A(s,a)$在实际应用时的公式如下所示:$$A(S_t,A_t)=R_{t+1}+\gamma{V(S_{t+1})}-V(S_t)$$因此Critic只需要更新和计算state value $\hat{v}(s,w)$即可。 具体计算公式如下:$$\text{Policy Update: }\Delta \theta=\alpha \nabla_{\theta}\left(\log \pi\left(S_{t}, A_{t}, \theta\right)\right) \left[R_{t+1}+\gamma{\hat{v}(S_{t+1},w)}-\hat{v}(S_t,w)\right]$$
$$\text{Value Update: }\Delta {w}=\beta\left[R_{t+1}+\gamma{\hat{v}(S_{t+1},w)}-\hat{v}(S_t,w)\right] \nabla_{w} \hat{v}\left(S_{t}, w\right)$$使用该算法的一个具体的例子可以参考该文件,文件使用的gym环境为MountainCarContinuous-v0。
DDPG
DDPG(Deep Deterministic Policy Gradients)方法是一种基于Actor-Critic框架的方法,该方法适用于连续的动作空间,得到的策略是一个确定性策略(i.e., $\pi(s)=a$),但是通过在动作上加入一些噪音产生一定的随机性,有利于对整个动作空间的探索。DDPG具有较高的学习和训练效率,常被用于机械控制等方面。Actor部分用来计算并更新策略$\pi(s,\theta)$,Critic部分用来计算并更新action value $\hat{q}(s,a,w)$,和上一部分中的Critic区别不大,但是使用了Fixed Q-targets这一技术(具体介绍见上篇文章):$$A_t=\pi(S_t,\theta)+\mathcal{N}_t\text{, }\mathcal{N}\text{ is a random process}$$
$$\Delta {w}=\beta\left(R_{t+1}+\gamma \hat{q}\left(S_{t+1}, \pi(S_{t+1},\theta^{\prime}), w^{\prime}\right)-\hat{q}\left(S_{t}, A_{t}, w\right)\right) \nabla_{w} \hat{q}\left(S_{t}, A_{t}, w\right)$$针对策略梯度的求解,令$J(\theta)=E_{\rho(s)}[\hat{q}(s,a,w)]=E_{\rho(s)}[\hat{q}(s,\pi(s,\theta),w)]$,其中$\rho(s)$为状态$s$的分布。利用链式法则,参数$\theta$的更新规则如下:$$\Delta \theta=\alpha \nabla_{a}\hat{q}(S_t,a,w)|_{a=\pi(S_t,\theta)}\nabla_{\theta}[\pi(S_t,\theta)]$$此外对target networks中的参数$w^{\prime},\theta^{\prime}$,使用soft update的策略,即每次更新$w,\theta$后,有$$w^{\prime}=\tau{w}+(1-\tau)w^{\prime}\text{, }\theta^{\prime}=\tau{\theta}+(1-\tau)\theta^{\prime}$$
代码实现
使用的环境是关于四轴飞行器的控制问题,飞行器共有四个马达来提供推力,它们之间的相互配合使得飞行器可以完成多种飞行动作,飞行器的控制代码如下:
import numpy as np import csv def C(x): return np.cos(x) def S(x): return np.sin(x) def earth_to_body_frame(ii, jj, kk): # C^b_n R = [[C(kk) * C(jj), C(kk) * S(jj) * S(ii) - S(kk) * C(ii), C(kk) * S(jj) * C(ii) + S(kk) * S(ii)], [S(kk) * C(jj), S(kk) * S(jj) * S(ii) + C(kk) * C(ii), S(kk) * S(jj) * C(ii) - C(kk) * S(ii)], [-S(jj), C(jj) * S(ii), C(jj) * C(ii)]] return np.array(R) def body_to_earth_frame(ii, jj, kk): # C^n_b return np.transpose(earth_to_body_frame(ii, jj, kk)) class PhysicsSim(): def __init__(self, init_pose=None, init_velocities=None, init_angle_velocities=None, runtime=5.): self.init_pose = init_pose self.init_velocities = init_velocities self.init_angle_velocities = init_angle_velocities self.runtime = runtime self.gravity = -9.81 # m/s self.rho = 1.2 self.mass = 0.958 # 300 g self.dt = 1 / 50.0 # Timestep self.C_d = 0.3 self.l_to_rotor = 0.4 self.propeller_size = 0.1 width, length, height = .51, .51, .235 self.dims = np.array([width, length, height]) # x, y, z dimensions of quadcopter self.areas = np.array([length * height, width * height, width * length]) I_x = 1 / 12. * self.mass * (height**2 + width**2) I_y = 1 / 12. * self.mass * (height**2 + length**2) # 0.0112 was a measured value I_z = 1 / 12. * self.mass * (width**2 + length**2) self.moments_of_inertia = np.array([I_x, I_y, I_z]) # moments of inertia env_bounds = 300.0 # 300 m / 300 m / 300 m self.lower_bounds = np.array([-env_bounds / 2, -env_bounds / 2, 0]) self.upper_bounds = np.array([env_bounds / 2, env_bounds / 2, env_bounds]) self.reset() def reset(self): self.time = 0.0 self.pose = np.array([0.0, 0.0, 10.0, 0.0, 0.0, 0.0]) if self.init_pose is None else np.copy(self.init_pose) self.v = np.array([0.0, 0.0, 0.0]) if self.init_velocities is None else np.copy(self.init_velocities) self.angular_v = np.array([0.0, 0.0, 0.0]) if self.init_angle_velocities is None else np.copy(self.init_angle_velocities) self.linear_accel = np.array([0.0, 0.0, 0.0]) self.angular_accels = np.array([0.0, 0.0, 0.0]) self.prop_wind_speed = np.array([0., 0., 0., 0.]) self.done = False def find_body_velocity(self): body_velocity = np.matmul(earth_to_body_frame(*list(self.pose[3:])), self.v) return body_velocity def get_linear_drag(self): linear_drag = 0.5 * self.rho * self.find_body_velocity()**2 * self.areas * self.C_d return linear_drag def get_linear_forces(self, thrusts): # Gravity gravity_force = self.mass * self.gravity * np.array([0, 0, 1]) # Thrust thrust_body_force = np.array([0, 0, sum(thrusts)]) # Drag drag_body_force = -self.get_linear_drag() body_forces = thrust_body_force + drag_body_force linear_forces = np.matmul(body_to_earth_frame(*list(self.pose[3:])), body_forces) linear_forces += gravity_force return linear_forces def get_moments(self, thrusts): # (thrusts[2] + thrusts[3] - thrusts[0] - thrusts[1]) * self.T_q]) # Moment from thrust thrust_moment = np.array([(thrusts[3] - thrusts[2]) * self.l_to_rotor,(thrusts[1] - thrusts[0]) * self.l_to_rotor, 0]) drag_moment = self.C_d * 0.5 * self.rho * self.angular_v * np.absolute(self.angular_v) * self.areas * self.dims * self.dims moments = thrust_moment - drag_moment # + motor_inertia_moment return moments def calc_prop_wind_speed(self): body_velocity = self.find_body_velocity() phi_dot, theta_dot = self.angular_v[0], self.angular_v[1] s_0 = np.array([0., 0., theta_dot * self.l_to_rotor]) s_1 = -s_0 s_2 = np.array([0., 0., phi_dot * self.l_to_rotor]) s_3 = -s_2 speeds = [s_0, s_1, s_2, s_3] for num in range(4): perpendicular_speed = speeds[num] + body_velocity self.prop_wind_speed[num] = perpendicular_speed[2] def get_propeler_thrust(self, rotor_speeds): ### calculates net thrust (thrust - drag) based on velocity of propeller and incoming power thrusts = [] for prop_number in range(4): V = self.prop_wind_speed[prop_number] D = self.propeller_size n = rotor_speeds[prop_number] J = V / n * D # From http://m-selig.ae.illinois.edu/pubs/BrandtSelig-2011-AIAA-2011-1255-LRN-Propellers.pdf C_T = max(.12 - .07*max(0, J)-.1*max(0, J)**2, 0) thrusts.append(C_T * self.rho * n**2 * D**4) return thrusts def next_timestep(self, rotor_speeds): self.calc_prop_wind_speed() thrusts = self.get_propeler_thrust(rotor_speeds) self.linear_accel = self.get_linear_forces(thrusts) / self.mass position = self.pose[:3] + self.v * self.dt + 0.5 * self.linear_accel * self.dt**2 self.v += self.linear_accel * self.dt moments = self.get_moments(thrusts) self.angular_accels = moments / self.moments_of_inertia angles = self.pose[3:] + self.angular_v * self.dt + 0.5 * self.angular_accels * self.angular_accels * self.dt ** 2 angles = (angles + 2 * np.pi) % (2 * np.pi) self.angular_v = self.angular_v + self.angular_accels * self.dt new_positions = [] for ii in range(3): if position[ii] <= self.lower_bounds[ii]: new_positions.append(self.lower_bounds[ii]) self.done = True elif position[ii] > self.upper_bounds[ii]: new_positions.append(self.upper_bounds[ii]) self.done = True else: new_positions.append(position[ii]) self.pose = np.array(new_positions + list(angles)) self.time += self.dt if self.time > self.runtime: self.done = True return self.done
接下来选取起飞动作做为需要训练飞行器完成的任务。飞行器的动作由四个发动机施加的推力$(v_1,v_2,v_3,v_4)$构成,为了保证飞行动作的连续性,将同一个动作重复三个时间步,飞行器的状态由这三步的空间坐标以及飞行角度构成:$(x_i,y_i,z_i,\phi_i,\theta_i,\psi_i),\text{ }i=1,2,3$,具体代码和奖励函数如下:
class Task(): ### Task (environment) that defines the goal and provides feedback to the agent def __init__(self, init_pose=None, init_velocities=None, init_angle_velocities=None, runtime=5., target_pos=None): """Initialize a Task object. Params ====== init_pose: initial position of the quadcopter in (x,y,z) dimensions and the Euler angles init_velocities: initial velocity of the quadcopter in (x,y,z) dimensions init_angle_velocities: initial radians/second for each of the three Euler angles runtime: time limit for each episode target_pos: target/goal (x,y,z) position for the agent """ # Simulation self.sim = PhysicsSim(init_pose, init_velocities, init_angle_velocities, runtime) self.action_repeat = 3 # repeat the same action for 3 timesteps self.state_size = self.action_repeat * 6 self.action_low = 0 self.action_high = 900 self.action_size = 4 # Goal self.target_pos = target_pos if target_pos is not None else np.array([0., 0., 10.]) def get_reward(self, done): ### Uses current pose of sim to return reward done_final = done #reward = zero for matching target z, <0 as you go farther, upto -20 reward = -min(abs(self.target_pos[2] - self.sim.pose[2]), 20.0) if done_final: reward -= 10.0 elif self.sim.pose[2] >= self.target_pos[2]: # agent has crossed the target height reward += 10.0 # bonus reward done_final = True return reward, done_final def step(self, actions): ### Uses action to obtain next state, reward, done reward = 0 pose_all = [] rotor_speeds = [a*(self.action_high-self.action_low)+self.action_low for a in actions] for _ in range(self.action_repeat): done = self.sim.next_timestep(rotor_speeds) # update the sim pose and velocities r,done_final = self.get_reward(done) reward += r pose_all = pose_all + list(self.sim.pose) next_state = np.array(pose_all) return next_state, reward, done_final def reset(self): ### Reset the sim to start a new episode self.sim.reset() pose_all = list(self.sim.pose) * self.action_repeat state = np.array(pose_all) return state
对于随机过程$\mathcal{N}$,采用Ornstein-Uhlenbeck过程,此外在训练过程中还使用了上篇文章中介绍的Experience Replay,具体代码如下:
class OUNoise: ### Ornstein-Uhlenbeck process def __init__(self, size, mu, theta, sigma): """Initialize parameters and noise process.""" self.mu = mu * np.ones(size) self.theta = theta self.sigma = sigma self.reset() def reset(self): """Reset the internal state (= noise) to mean (mu).""" self.state = copy.copy(self.mu) def sample(self): """Update internal state and return it as a noise sample.""" x = self.state dx = self.theta * (self.mu - x) + self.sigma * np.random.randn(len(x)) self.state = x + dx return self.state class ReplayBuffer: ### Fixed-size buffer to store experience tuples def __init__(self, buffer_size, batch_size): """Initialize a ReplayBuffer object. Params ====== buffer_size: maximum size of buffer batch_size: size of each training batch """ self.memory = deque(maxlen=buffer_size) # internal memory (deque) self.batch_size = batch_size self.experience = namedtuple("Experience", field_names=["state", "action", "reward", "next_state", "done"]) def add(self, state, action, reward, next_state, done): ### Add a new experience to memory e = self.experience(state, action, reward, next_state, done) self.memory.append(e) def sample(self, batch_size=64): ### Randomly sample a batch of experiences from memory return random.sample(self.memory, k=self.batch_size) def __len__(self): ### Return the current size of internal memory return len(self.memory)
接下来对Actor、Critic以及DDPG建立模型:
- Actor
 View Code
View Codeimport copy import random from collections import namedtuple, deque from keras import layers, models, optimizers, initializers, regularizers from keras import backend as K class Actor: ### Actor (Policy) Model def __init__(self, state_size, action_size): """Initialize parameters and build model. Params ====== state_size (int): Dimension of each state action_size (int): Dimension of each action """ self.state_size = state_size self.action_size = action_size self.build_model() # Initialize any other variables here def build_model(self): ### Build an actor (policy) network that maps states -> actions states = layers.Input(shape=(self.state_size,), name='states') # Define input layer (states) # Add hidden layers net = layers.Dense(units=400, activation='relu')(states) net = layers.Dense(units=300, activation='relu')(net) # Add final output layer with sigmoid activation actions = layers.Dense(units=self.action_size, activation='sigmoid', bias_initializer='zeros', name='actions', \ kernel_initializer=initializers.RandomUniform(minval=-0.0001, maxval=0.0001))(net) # Create Keras model self.model = models.Model(inputs=states, outputs=actions) # Define loss function using action value (Q value) gradients action_gradients = layers.Input(shape=(self.action_size,)) loss = K.mean(-action_gradients * actions) # Define optimizer and training function optimizer = optimizers.Adam(lr=0.0001) updates_op = optimizer.get_updates(params=self.model.trainable_weights, loss=loss) self.train_fn = K.function(inputs=[self.model.input, action_gradients, K.learning_phase()], \ outputs=[], updates=updates_op)
- Critic
 View Code
View Codeclass Critic: ### Critic (Value) Model def __init__(self, state_size, action_size): """Initialize parameters and build model. Params ====== state_size (int): Dimension of each state action_size (int): Dimension of each action """ self.state_size = state_size self.action_size = action_size self.build_model() # Initialize any other variables here def build_model(self): ### Build a critic (value) network that maps (state, action) pairs -> Q-values states = layers.Input(shape=(self.state_size,), name='states') # Define input layers actions = layers.Input(shape=(self.action_size,), name='actions') # Add hidden layer(s) for state pathway net_states = layers.Dense(units=400, activation='relu')(states) net_states = layers.Dense(units=300)(net_states) # Add hidden layer(s) for action pathway net_actions = layers.Dense(units=300)(actions) # Combine state and action pathways net = layers.Add()([net_states, net_actions]) net = layers.Activation('relu')(net) # Add final output layer to prduce action values (Q values) Q_values = layers.Dense(units=1, name='q_values')(net) # Create Keras model self.model = models.Model(inputs=[states, actions], outputs=Q_values) # Define optimizer and compile model for training with built-in loss function optimizer = optimizers.Adam(lr=0.01) self.model.compile(optimizer=optimizer, loss='mse') # Compute action gradients (derivative of Q values w.r.t. to actions) action_gradients = K.gradients(Q_values, actions) # one element list:[tensor shape=(batch_size,4)] # Define an additional function to fetch action gradients (to be used by actor model) self.get_action_gradients = K.function(inputs=[*self.model.input, K.learning_phase()], \ outputs=action_gradients)
- DDPG
 View Code
View Codeclass DDPG(): ### Reinforcement Learning agent that learns using DDPG def __init__(self, task): self.task = task self.state_size = task.state_size self.action_size = task.action_size # Actor (Policy) Model self.actor_local = Actor(self.state_size, self.action_size) self.actor_target = Actor(self.state_size, self.action_size) # Critic (Value) Model self.critic_local = Critic(self.state_size, self.action_size) self.critic_target = Critic(self.state_size, self.action_size) # Initialize target model parameters with local model parameters self.critic_target.model.set_weights(self.critic_local.model.get_weights()) self.actor_target.model.set_weights(self.actor_local.model.get_weights()) # Noise process self.exploration_mu = 0 self.exploration_theta = 1.0 self.exploration_sigma = 0.01 self.noise = OUNoise(self.action_size, self.exploration_mu, self.exploration_theta, self.exploration_sigma) # Replay memory self.buffer_size = 1000000 self.batch_size = 64 self.memory = ReplayBuffer(self.buffer_size, self.batch_size) # Algorithm parameters self.gamma = 0.99 # discount factor self.tau = 0.0002 # for soft update of target parameters def reset_episode(self): self.noise.reset() state = self.task.reset() self.last_state = state return state def step(self, action, reward, next_state, done): # Save experience self.memory.add(self.last_state, action, reward, next_state, done) # Learn, if enough samples are available in memory if len(self.memory) > self.batch_size: experiences = self.memory.sample() self.learn(experiences) # Roll over last state self.last_state = next_state def act(self, state, mode='train'): ### Returns actions for a given state as per current policy state = np.reshape(state, [-1, self.state_size]) #(1,state_size) action = self.actor_local.model.predict(state)[0] # add some noise for exploration return list(np.clip(action+self.noise.sample(), 0.01, 1)) if mode=='train' else list(np.clip(action, 0.01, 1)) def learn(self, experiences): ### Update policy and value parameters using given batch of experience tuples # Convert experience tuples to separate arrays for each element (states, actions, rewards, etc.) states = np.vstack([e.state for e in experiences if e is not None]) actions = np.array([e.action for e in experiences if e is not None]).astype(np.float32).reshape(-1, self.action_size) rewards = np.array([e.reward for e in experiences if e is not None]).astype(np.float32).reshape(-1, 1) dones = np.array([e.done for e in experiences if e is not None]).astype(np.uint8).reshape(-1, 1) next_states = np.vstack([e.next_state for e in experiences if e is not None]) # Get predicted next-state actions and Q values from target models # Q_targets_next = critic_target(next_state, actor_target(next_state)) actions_next = self.actor_target.model.predict_on_batch(next_states) Q_targets_next = self.critic_target.model.predict_on_batch([next_states, actions_next]) # Compute Q targets for current states and train critic model (local) Q_targets = rewards + self.gamma * Q_targets_next * (1 - dones) #set Q_targets_next=0 if done self.critic_local.model.train_on_batch(x=[states, actions], y=Q_targets) #在一个 batch 的数据上进行一次参数更新 # Train actor model (local) action_gradients = np.reshape(self.critic_local.get_action_gradients([states, actions, 0]), (-1, self.action_size)) self.actor_local.train_fn([states, action_gradients, 1]) # custom training function # Soft-update target models self.soft_update(self.critic_local.model, self.critic_target.model) self.soft_update(self.actor_local.model, self.actor_target.model) def soft_update(self, local_model, target_model): ### Soft update model parameters local_weights = np.array(local_model.get_weights()) target_weights = np.array(target_model.get_weights()) assert len(local_weights) == len(target_weights), "Local and target model parameters must have the same size" new_weights = self.tau * local_weights + (1 - self.tau) * target_weights target_model.set_weights(new_weights)
智能体的训练和测试过程如下所示:
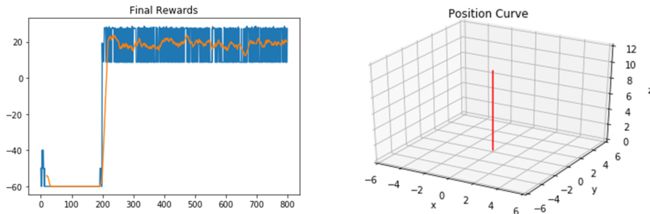
import sys import Task import DDPG from collections import defaultdict import pandas as pd import matplotlib.pyplot as plt ### Initialize the agent init_pose = np.zeros(6) target_pos = np.array([0., 0., 10.]) task = Task(init_pose=init_pose, target_pos=target_pos) agent = DDPG(task) ### Train num_episodes = 800 rewards = defaultdict(list) positions = defaultdict(list) actions = defaultdict(list) for i_episode in range(1, num_episodes+1): state = agent.reset_episode() # start a new episode positions[i_episode].append(state) while True: action = agent.act(state) next_state, reward, done = task.step(action) agent.step(action, reward, next_state, done) state = next_state #roll state actions[i_episode].append(action) rewards[i_episode].append(reward) positions[i_episode].append(next_state) if done: print("\rEpisode = {:4d}, Final Reward = {:7.3f}, Final Position = {}" \ .format(i_episode, rewards[i_episode][-1], positions[i_episode][-1][-6:-3]), end="") break sys.stdout.flush() ### Plot the final reward of each episode def plot_rewards(rewards, rolling_window=20): # Plot rewards and optional rolling mean using specified window plt.plot(rewards) plt.title("Final Rewards"); rolling_mean = pd.Series(rewards).rolling(rolling_window).mean() plt.plot(rolling_mean) rewards_p = np.array([rewards[i][-1] for i in range(1, num_episodes+1)]) plot_rewards(rewards_p) #左图 ### Simulate using the deterministic policy positions_sim = [] rewards_sim = [] actions_sim = [] state = agent.reset_episode() # start a new episode positions_sim.append(state) while True: action = agent.act(state, mode='test') next_state, reward, done = task.step(action) state = next_state #roll state actions_sim.append(action) rewards_sim.append(reward) positions_sim.append(next_state) if done: break ### Plot the position curve . from mpl_toolkits.mplot3d import Axes3D def plot_positions(xs,ys,zs): fig = plt.figure() ax = fig.gca(projection='3d') ax.set_title("Position Curve") ax.set_xlabel("x"); ax.set_xlim(-6,6) ax.set_ylabel("y"); ax.set_ylim(-6,6) ax.set_zlabel("z"); ax.set_zlim(0,12) ax.plot(xs, ys, zs, c='r') positions_p = np.array(positions_sim) plot_positions(positions_p[:,-6], positions_p[:,-5], positions_p[:,-4]) #右图 final_p = [round(p,3) for p in positions_p[-1,-6:-3]] print("The Final Reward = {:7.3f}".format(rewards_sim[-1])) #8.794 print('The Final Position is {}'.format(final_p)) #[-0.001, 0.0, 10.126]