持续优化中~~~
研究背景:
中国制酒历史源远流长,品种繁多,名酒荟萃,享誉中外。其中,黄酒跟白酒是两种主要的酒类。它们渗透于中华民族的源远流长的文明史中,对文学创作、文化娱乐、饮食文化的影响更是起到一个重要作用。但是,随着全球化的脚步,我们的生活中渐渐出现了红葡萄酒、白葡萄酒。喝葡萄酒渐渐成为一种时尚。百度了一下葡萄酒的功能,有如下:
1)葡萄酒中含有抗氧化成分和丰富的酚类化合物,可防止动脉硬化和血小板凝结,保护并维持心脑血管系统的正常生理机能,起到保护心脏、防止中风的作用;
2) 饮用葡萄酒对女性有很好的美容养颜的功效,可养气活血,使皮肤富有弹性。
好像还很不错的样子。在 UCI数据库中,发现一个关于葡萄酒质量评分的数据集,于是决定来探讨一下影响葡萄酒口感的因素是什么。
目的:
从UCI下载数据集:Wine Quality Data Set ,里面包含红葡萄酒和白葡萄酒的2个样本数据集。里面均包含葡萄酒的11个物理化学方面的因素,还有1个对葡萄酒质量的测评平均分数(0-10分)。现采用其白葡萄酒数据,对该数据集进行一定的数据分析:
(1)建立回归模型,研究这些性质是怎样影响白葡萄酒的质量评价
(2)找出影响较大的前三因素
(3)这些物理化学性质之间是否存在一定的关系
目录:
一.数据探索分析&数据预处理
二.建模分析
三.总结与建议
一.数据探索分析&数据预处理
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["font.sans-serif"]=["SimHei"] #正常显示中文标签
plt.rcParams["axes.unicode_minus"]=False #正常显示负号
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
#导入数据
data = pd.read_csv(r"G:\data\UCI data\Wine Quality\winequality-white.csv", sep=";")
下面先观察一下白葡萄酒数据:
data.head()
| fixed acidity | volatile acidity | citric acid | residual sugar | chlorides | free sulfur dioxide | total sulfur dioxide | density | pH | sulphates | alcohol | quality | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.0 | 0.27 | 0.36 | 20.7 | 0.045 | 45.0 | 170.0 | 1.0010 | 3.00 | 0.45 | 8.8 | 6 |
| 1 | 6.3 | 0.30 | 0.34 | 1.6 | 0.049 | 14.0 | 132.0 | 0.9940 | 3.30 | 0.49 | 9.5 | 6 |
| 2 | 8.1 | 0.28 | 0.40 | 6.9 | 0.050 | 30.0 | 97.0 | 0.9951 | 3.26 | 0.44 | 10.1 | 6 |
| 3 | 7.2 | 0.23 | 0.32 | 8.5 | 0.058 | 47.0 | 186.0 | 0.9956 | 3.19 | 0.40 | 9.9 | 6 |
| 4 | 7.2 | 0.23 | 0.32 | 8.5 | 0.058 | 47.0 | 186.0 | 0.9956 | 3.19 | 0.40 | 9.9 | 6 |
data.info()
RangeIndex: 4898 entries, 0 to 4897
Data columns (total 12 columns):
fixed acidity 4898 non-null float64
volatile acidity 4898 non-null float64
citric acid 4898 non-null float64
residual sugar 4898 non-null float64
chlorides 4898 non-null float64
free sulfur dioxide 4898 non-null float64
total sulfur dioxide 4898 non-null float64
density 4898 non-null float64
pH 4898 non-null float64
sulphates 4898 non-null float64
alcohol 4898 non-null float64
quality 4898 non-null int64
dtypes: float64(11), int64(1)
memory usage: 459.3 KB
1.数据集基本情况探索:
(1)数据集中总共有4898个白葡萄酒的样本数据。其中,包含11个物理化学的特征和1个葡萄酒质量评分。
分别为:
- fixed acidity 非挥发性酸
- volatile acidity 挥发性酸
- citric acid 柠檬酸
- residual sugar 剩余糖分
- chlorides 氯化物
- free sulfur dioxide 游离二氧化硫
- total sulfur dioxide 总二氧化硫
- density 密度
- pH 酸碱性
- sulphates 硫酸盐
- alcohol 酒精
- quality 质量
(2)数据完整,无缺失值。注意到,有些数值小于0.1,有些数值大于100。在做回归模型时,我们常用MSE(均方误差)来衡量模型的好坏,如果数据量纲不一样,可能影响我们对模型的评估,所以后面我们将对数据进行归一化处理,排除量纲带来的影响。
(3)11个因素均为浮点型数据,最后的质量评分为整型数据。
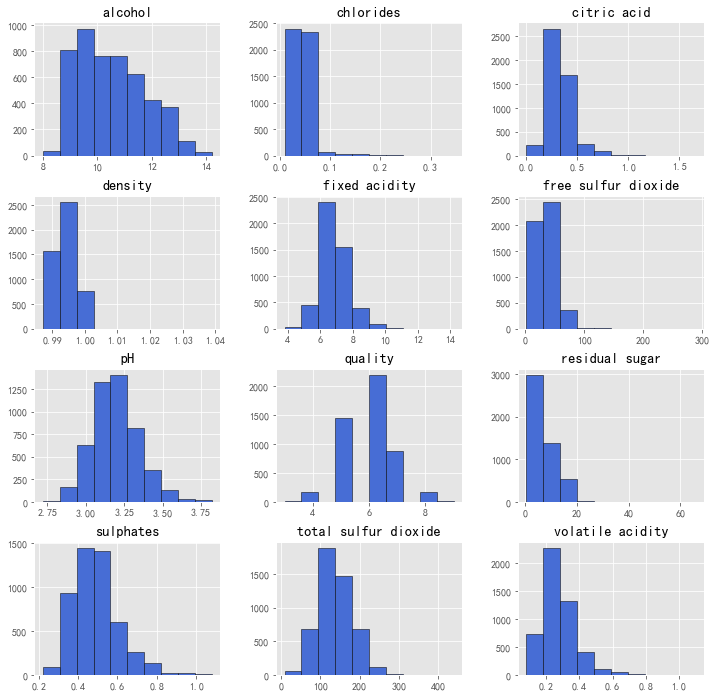
下面通过计算均值、方差、最小最大值等,配合数据的分布直方图来看数据的大致分布:
data.describe()
| fixed acidity | volatile acidity | citric acid | residual sugar | chlorides | free sulfur dioxide | total sulfur dioxide | density | pH | sulphates | alcohol | quality | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 | 4898.000000 |
| mean | 6.854788 | 0.278241 | 0.334192 | 6.391415 | 0.045772 | 35.308085 | 138.360657 | 0.994027 | 3.188267 | 0.489847 | 10.514267 | 5.877909 |
| std | 0.843868 | 0.100795 | 0.121020 | 5.072058 | 0.021848 | 17.007137 | 42.498065 | 0.002991 | 0.151001 | 0.114126 | 1.230621 | 0.885639 |
| min | 3.800000 | 0.080000 | 0.000000 | 0.600000 | 0.009000 | 2.000000 | 9.000000 | 0.987110 | 2.720000 | 0.220000 | 8.000000 | 3.000000 |
| 25% | 6.300000 | 0.210000 | 0.270000 | 1.700000 | 0.036000 | 23.000000 | 108.000000 | 0.991723 | 3.090000 | 0.410000 | 9.500000 | 5.000000 |
| 50% | 6.800000 | 0.260000 | 0.320000 | 5.200000 | 0.043000 | 34.000000 | 134.000000 | 0.993740 | 3.180000 | 0.470000 | 10.400000 | 6.000000 |
| 75% | 7.300000 | 0.320000 | 0.390000 | 9.900000 | 0.050000 | 46.000000 | 167.000000 | 0.996100 | 3.280000 | 0.550000 | 11.400000 | 6.000000 |
| max | 14.200000 | 1.100000 | 1.660000 | 65.800000 | 0.346000 | 289.000000 | 440.000000 | 1.038980 | 3.820000 | 1.080000 | 14.200000 | 9.000000 |
plt.style.use("ggplot")
data.hist(figsize=(12,12), color="#476DD5", edgecolor="k")
array([[,
,
],
[,
,
],
[,
,
],
[,
,
]], dtype=object)
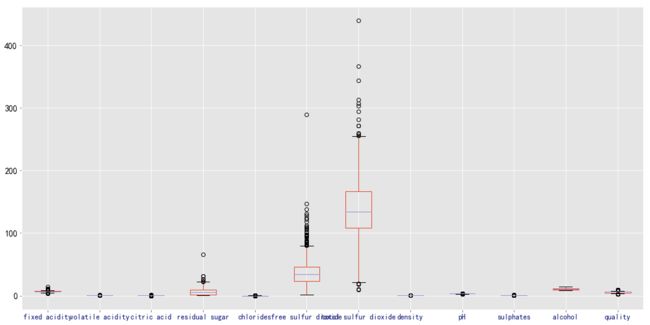
data.boxplot(figsize=(18,9))
plt.yticks(fontsize=14,color="k")
plt.xticks(fontsize=12,color="#081073")
(array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]),
)
sns.pairplot(data)
data.skew().sort_values(ascending=False)
chlorides 5.023331
volatile acidity 1.576980
free sulfur dioxide 1.406745
citric acid 1.281920
residual sugar 1.077094
density 0.977773
sulphates 0.977194
fixed acidity 0.647751
alcohol 0.487342
pH 0.457783
total sulfur dioxide 0.390710
quality 0.155796
dtype: float64
data.kurt().sort_values(ascending=False)
chlorides 37.564600
free sulfur dioxide 11.466342
density 9.793807
citric acid 6.174901
volatile acidity 5.091626
residual sugar 3.469820
fixed acidity 2.172178
sulphates 1.590930
total sulfur dioxide 0.571853
pH 0.530775
quality 0.216526
alcohol -0.698425
dtype: float64
(data.max()-data.min()).sort_values(ascending=False)
total sulfur dioxide 431.00000
free sulfur dioxide 287.00000
residual sugar 65.20000
fixed acidity 10.40000
alcohol 6.20000
quality 6.00000
citric acid 1.66000
pH 1.10000
volatile acidity 1.02000
sulphates 0.86000
chlorides 0.33700
density 0.05187
dtype: float64
2.从均值、标准差、四分位数等值,及直方图看到:
(1)所有的特征都不是正态分布,均呈现右偏。chlorides(氯化物)的右偏程度最大,为5.02,接着是volatile acidity(挥发性酸):1.58 、free sulfur dioxide(游离二氧化硫):1.41;右偏最小的三个特征为:total sulfur dioxide(总二氧化硫0.39)< PH(酸碱度0.46)< alcohol(酒精0.49)。
(2)每个特征的极差(最大值减去最小值的值)相差较大,最大的为total sulfur dioxide(总二氧化硫):431,最小的为density(密度),仅为0.05。后面将对数据进行归一化处理,消除量纲影响。
(3)从四分位数来看,可能存在异常值。从箱线图来看,存在较多的较大的值。为了便于观察,下面进行归一化,借用箱线图更细致来看数据的集中分布情况、异常值的情况。
(4)质量评分最小值为3,最大值为9。50%的评分为5或6分,看出大多数白葡萄酒质量处于中等水平,不会太差,也不会太好。
(5)看到大多数变量之间的关系较小,下面通过具体的数值及热力图做更深入探讨。
3.下面对数据进行标准化处理,让数据减去其均值再除以其对应的标准差:
from sklearn.preprocessing import scale
data_scaled = scale(data)
data_scaled
array([[ 1.72096961e-01, -8.17699008e-02, 2.13280202e-01, ...,
-3.49184257e-01, -1.39315246e+00, 1.37870140e-01],
[ -6.57501128e-01, 2.15895632e-01, 4.80011213e-02, ...,
1.34184656e-03, -8.24275678e-01, 1.37870140e-01],
[ 1.47575110e+00, 1.74519434e-02, 5.43838363e-01, ...,
-4.36815783e-01, -3.36667007e-01, 1.37870140e-01],
...,
[ -4.20473102e-01, -3.79435433e-01, -1.19159198e+00, ...,
-2.61552731e-01, -9.05543789e-01, 1.37870140e-01],
[ -1.60561323e+00, 1.16673788e-01, -2.82557040e-01, ...,
-9.62604939e-01, 1.85757201e+00, 1.26711420e+00],
[ -1.01304317e+00, -6.77100966e-01, 3.78559282e-01, ...,
-1.48839409e+00, 1.04489089e+00, 1.37870140e-01]])
plt.figure(figsize=(17,8))
columns = ["非挥发性酸","挥发性酸","柠檬酸","剩余糖分","氯化物","游离二氧化硫","总二氧化硫",
"密度","酸碱性","硫酸盐","酒精","质量"]
plt.boxplot(data_scaled,
showmeans=True,meanprops={"marker":"D","markerfacecolor":"red"},#设置均值点的属性,点的形状、填充色
labels=columns
)
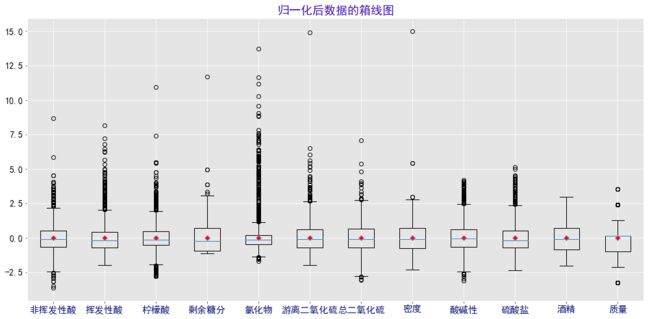
plt.title("归一化后数据的箱线图",color="#4013AF",size=18)
plt.yticks(fontsize=14,color="k")
plt.xticks(fontsize=14.5,color="#081073")
(array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]),
)
data_scaled = pd.DataFrame(data_scaled)
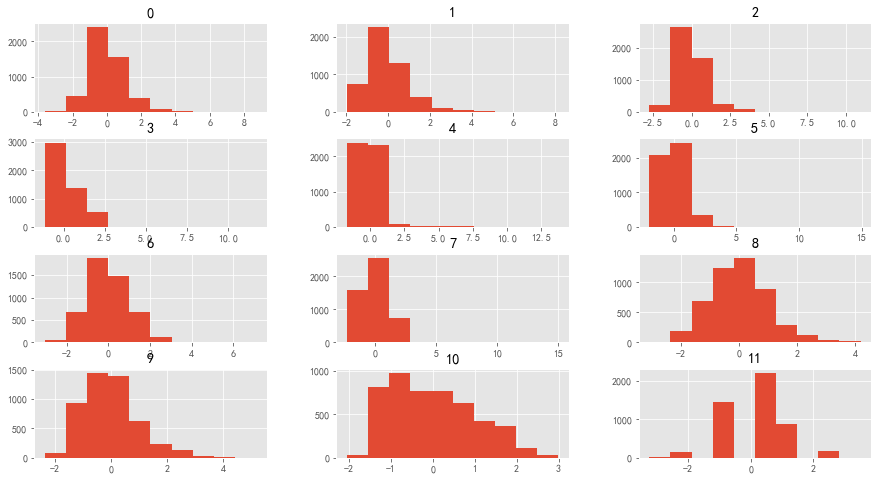
data_scaled.hist(figsize=(15,8))
array([[,
,
],
[,
,
],
[,
,
],
[,
,
]], dtype=object)
data_scaled.skew().sort_values(ascending=False)
4 5.023331
1 1.576980
5 1.406745
2 1.281920
3 1.077094
7 0.977773
9 0.977194
0 0.647751
10 0.487342
8 0.457783
6 0.390710
11 0.155796
dtype: float64
data_scaled.kurt().sort_values(ascending=False)
4 37.564600
5 11.466342
7 9.793807
2 6.174901
1 5.091626
3 3.469820
0 2.172178
9 1.590930
6 0.571853
8 0.530775
11 0.216526
10 -0.698425
dtype: float64
(data_scaled.max()-data_scaled.min()).sort_values(ascending=False)
7 17.344336
5 16.876991
4 15.426350
2 13.718164
3 12.856056
0 12.325457
6 10.142674
1 10.120628
9 7.536311
8 7.285483
11 6.775464
10 5.038623
dtype: float64
4.对数据进行归一化后:
绘制箱线图后发现,除了酒精,其余的变量都存在异常值,且普遍存在较多较大的异常值。
(1)其中,氯化物的箱体最扁,说明50%的数据在均值附近波动,但是存在大量较大的异常值,偏离均值分布。
(2)而剩余糖分、总二氧化硫、密度、质量评分的异常值相对其他特征来说,比较少,且普遍远大于平均值。
(3)非挥发性酸、柠檬酸、酸碱性这三个特征都存在大量较大的异常值,但也同时存在部分较小的异常值。
(4)挥发性酸、氯化物、游离二氧化硫、硫酸盐这四个特征的异常值普遍较大,只有氯化物存在少量较小的异常值。
(5)酒精特征不存在异常值,也与归一前所做的直方图对应得上。
(6)归一化后数据的偏度、峰度均没有改变,但是它将数据按照一定的规则缩小了,使得采用MSE来评价更有参考意义。
5.下面探究一下,各特征间、各特征与质量评分之间的关系:
data_df_scaled = pd.DataFrame(data_scaled)
data_df_scaled.columns = columns
data_df_scaled.sample(4) #随机抽取5个归一化后的样本数据
| 非挥发性酸 | 挥发性酸 | 柠檬酸 | 剩余糖分 | 氯化物 | 游离二氧化硫 | 总二氧化硫 | 密度 | 酸碱性 | 硫酸盐 | 酒精 | 质量 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 819 | -0.301959 | 2.795664 | -0.943673 | 0.494640 | -0.538886 | -0.488556 | -0.126152 | 0.910393 | 0.077712 | 0.176605 | -1.149348 | -0.991374 |
| 905 | 1.831293 | -0.875545 | 0.709117 | -0.944765 | 0.056196 | -1.547043 | -0.879204 | -0.009154 | -0.849531 | 1.403446 | 0.476014 | -2.120618 |
| 4391 | 0.527639 | -0.577879 | 0.295920 | 1.796020 | 0.101972 | 2.040053 | 1.521150 | 1.659406 | 0.408870 | 2.455025 | -0.905544 | -0.991374 |
| 2314 | 0.172097 | -0.875545 | -0.034638 | -0.018025 | -0.630437 | 0.393517 | -0.267349 | -0.738104 | 0.806260 | -0.962605 | 1.369963 | 0.137870 |
corr_df = data_df_scaled.corr()
corr_df
| 非挥发性酸 | 挥发性酸 | 柠檬酸 | 剩余糖分 | 氯化物 | 游离二氧化硫 | 总二氧化硫 | 密度 | 酸碱性 | 硫酸盐 | 酒精 | 质量 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 非挥发性酸 | 1.000000 | -0.022697 | 0.289181 | 0.089021 | 0.023086 | -0.049396 | 0.091070 | 0.265331 | -0.425858 | -0.017143 | -0.120881 | -0.113663 |
| 挥发性酸 | -0.022697 | 1.000000 | -0.149472 | 0.064286 | 0.070512 | -0.097012 | 0.089261 | 0.027114 | -0.031915 | -0.035728 | 0.067718 | -0.194723 |
| 柠檬酸 | 0.289181 | -0.149472 | 1.000000 | 0.094212 | 0.114364 | 0.094077 | 0.121131 | 0.149503 | -0.163748 | 0.062331 | -0.075729 | -0.009209 |
| 剩余糖分 | 0.089021 | 0.064286 | 0.094212 | 1.000000 | 0.088685 | 0.299098 | 0.401439 | 0.838966 | -0.194133 | -0.026664 | -0.450631 | -0.097577 |
| 氯化物 | 0.023086 | 0.070512 | 0.114364 | 0.088685 | 1.000000 | 0.101392 | 0.198910 | 0.257211 | -0.090439 | 0.016763 | -0.360189 | -0.209934 |
| 游离二氧化硫 | -0.049396 | -0.097012 | 0.094077 | 0.299098 | 0.101392 | 1.000000 | 0.615501 | 0.294210 | -0.000618 | 0.059217 | -0.250104 | 0.008158 |
| 总二氧化硫 | 0.091070 | 0.089261 | 0.121131 | 0.401439 | 0.198910 | 0.615501 | 1.000000 | 0.529881 | 0.002321 | 0.134562 | -0.448892 | -0.174737 |
| 密度 | 0.265331 | 0.027114 | 0.149503 | 0.838966 | 0.257211 | 0.294210 | 0.529881 | 1.000000 | -0.093591 | 0.074493 | -0.780138 | -0.307123 |
| 酸碱性 | -0.425858 | -0.031915 | -0.163748 | -0.194133 | -0.090439 | -0.000618 | 0.002321 | -0.093591 | 1.000000 | 0.155951 | 0.121432 | 0.099427 |
| 硫酸盐 | -0.017143 | -0.035728 | 0.062331 | -0.026664 | 0.016763 | 0.059217 | 0.134562 | 0.074493 | 0.155951 | 1.000000 | -0.017433 | 0.053678 |
| 酒精 | -0.120881 | 0.067718 | -0.075729 | -0.450631 | -0.360189 | -0.250104 | -0.448892 | -0.780138 | 0.121432 | -0.017433 | 1.000000 | 0.435575 |
| 质量 | -0.113663 | -0.194723 | -0.009209 | -0.097577 | -0.209934 | 0.008158 | -0.174737 | -0.307123 | 0.099427 | 0.053678 | 0.435575 | 1.000000 |
corr_df["质量"].sort_values(ascending=False)
质量 1.000000
酒精 0.435575
酸碱性 0.099427
硫酸盐 0.053678
游离二氧化硫 0.008158
柠檬酸 -0.009209
剩余糖分 -0.097577
非挥发性酸 -0.113663
总二氧化硫 -0.174737
挥发性酸 -0.194723
氯化物 -0.209934
密度 -0.307123
Name: 质量, dtype: float64
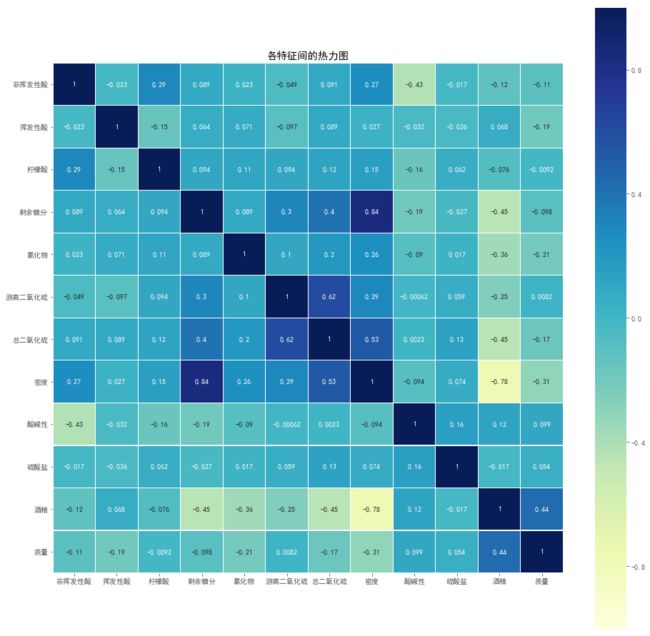
plt.figure(figsize=(16,16))
sns.heatmap(corr_df,linewidths=0.1,square=True,linecolor="white",annot=True,cmap='YlGnBu',vmin=-1,vmax=1)
plt.title("各特征间的热力图")
6.可以看到:
(1)白葡萄酒的质量评分与酒精、酸碱性、硫酸盐、游离二氧化硫有正的线性相关关系,它们的含量越高,口感评分越高;而与其他特征都呈现负的线性相关关系,这些特征的含量越高,口感评分越低。关系强度最大为0.44,大部分关系强度的绝对值均小于0.2(线性关系强度在[0,1]之间)。
(2)白葡萄酒的质量评分跟酒精、密度、氯化物的线性关系较强。质量评分与酒精之间有正相关关系,关系强度为0.44,酒精含量越高,口感评分越高;而与密度、氯化物为负线性相关关系,分别为-0.31、-0.21,它们的含量越高,白葡萄酒的口感评分越低。
(3)从热力图看,颜色普遍较浅,说明各变量间的线性相关关系较弱。
(4)而密度跟剩余糖分、酒精线性相关关系比较强。密度与剩余糖分的线性关系为0.84,剩余糖分越多,白葡萄酒的密度越大;密度与酒精的线性关系为-0.78,酒精密度越大,白葡萄酒的密度越小。
二.建模分析
1.一般线性模型
from sklearn.model_selection import train_test_split
xx_train, xx_test, yy_train, yy_test = train_test_split(data_df_scaled.iloc[:,:11], data_df_scaled.iloc[:,-1], test_size=0.3,random_state=100)
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
LR = LinearRegression()
LR.fit(xx_train, yy_train)
print("1.线性回归方程的截距:", LR.intercept_)
print("2.线性回归方程的回归系数:\n", LR.coef_)
yy0_pred = LR.predict(xx_test)
print("3.均方误差: ", mean_squared_error(yy_test, yy0_pred))
1.线性回归方程的截距: -0.00695101212555
2.线性回归方程的回归系数:
[ 7.63074915e-02 -1.93903082e-01 7.78570075e-03 4.68097575e-01
-4.05515219e-04 9.52752806e-02 -2.27524242e-02 -5.00567332e-01
1.27837888e-01 9.45724618e-02 2.90086677e-01]
3.均方误差: 0.724247388354
Coef0_df = pd.DataFrame(LR.intercept_,index=columns[0:11],columns=["回归系数"])
Coef0_df.sort_values(by="回归系数",ascending=False)
| 回归系数 | |
|---|---|
| 非挥发性酸 | -0.006951 |
| 挥发性酸 | -0.006951 |
| 柠檬酸 | -0.006951 |
| 剩余糖分 | -0.006951 |
| 氯化物 | -0.006951 |
| 游离二氧化硫 | -0.006951 |
| 总二氧化硫 | -0.006951 |
| 密度 | -0.006951 |
| 酸碱性 | -0.006951 |
| 硫酸盐 | -0.006951 |
| 酒精 | -0.006951 |
从拟合出来的结果来看,每个自变量的回归系数都很小,而且均为负值,与现实意义不符,该模型可能存在过拟合。下面用Lasso回归和Ridge回归来改善过拟合现象。
2.套索模型(LassoCV)
2.1 部分数据做交叉验证
from sklearn.linear_model import LassoCV
L1_CV = LassoCV(cv=10).fit(xx_train, yy_train)
yy1_pred = L1_CV.predict(xx_test)
print("均方误差:",mean_squared_error(yy_test, yy1_pred))
均方误差: 0.723045110072
Coef1_df = pd.DataFrame(L1_CV.intercept_,index=columns[0:11],columns=["回归系数"])
Coef1_df.sort_values(by="回归系数",ascending=False)
| 回归系数 | |
|---|---|
| 非挥发性酸 | -0.007413 |
| 挥发性酸 | -0.007413 |
| 柠檬酸 | -0.007413 |
| 剩余糖分 | -0.007413 |
| 氯化物 | -0.007413 |
| 游离二氧化硫 | -0.007413 |
| 总二氧化硫 | -0.007413 |
| 密度 | -0.007413 |
| 酸碱性 | -0.007413 |
| 硫酸盐 | -0.007413 |
| 酒精 | -0.007413 |
回归系数依然全部为负值且很小,说明做交叉验证的效果不好。下面我们拿所有的数据来做交叉验证,并用里面的属性来评估效果。
2.2 所有数据做交叉验证
x = data_df_scaled.iloc[:,:11]
y = data_df_scaled.iloc[:,-1]
print("特征集:",x.shape)
print("标签集:",y.shape)
from sklearn.linear_model import LassoCV
Las_cv = LassoCV(cv=10).fit(x,y)
特征集: (4898, 11)
标签集: (4898,)
print("线性模型的截距:",Las_cv.intercept_)
print("线性模型的回归系数:\n",Las_cv.coef_)
线性模型的截距: 1.06646156739e-14
线性模型的回归系数:
[ 0.0098704 -0.21381849 0. 0.33369253 -0.01166061 0.06691956
-0.009035 -0.31407498 0.07341963 0.06597724 0.352643 ]
Coef2_df = pd.DataFrame(Las_cv.coef_,index=columns[0:11],columns=["回归系数"])
Coef2_df.sort_values(by="回归系数",ascending=False)
| 回归系数 | |
|---|---|
| 酒精 | 0.352643 |
| 剩余糖分 | 0.333693 |
| 酸碱性 | 0.073420 |
| 游离二氧化硫 | 0.066920 |
| 硫酸盐 | 0.065977 |
| 非挥发性酸 | 0.009870 |
| 柠檬酸 | 0.000000 |
| 总二氧化硫 | -0.009035 |
| 氯化物 | -0.011661 |
| 挥发性酸 | -0.213818 |
| 密度 | -0.314075 |
A.可以看到,基于归一化后的数据:
(1)我们构造的模型为:
y_scaled = 1.06646156739e-14 + 0.0098704 * x1_scaled - 0.21381849 * x2_scaled + 0.33369253 * x4_scaled -
0.01166061 * x5_scaled + 0.06691956 * x6_scaled - 0.009035 * x7_scaled - 0.31407498 * x8_scaled +
0.07341963 * x9_scaled + 0.06597724 * x10_scaled + 0.352643 * x11_scaled
(2)柠檬酸的回归系数为0,在LasscoCV模型里,没有对白葡萄酒的口感评价产生影响。酒精、剩余糖分、酸碱性、游离二氧化硫、硫酸盐、非挥发性酸这6个特征对提升口感评价有正向作用,其影响力依次递减;在一定程度上,这些成分含量越多,口感越好。另一方面,密度、挥发性酸、氯化物、总二硫化物对提升口感有负作用,其影响力依次递减;一定程度上,它们在白葡萄酒里的含量越高,口感越差。
(3)对提升白葡萄酒口感评价影响最大的三个特征为:酒精含量、剩余糖分、酸碱性。酒精含量、剩余糖分含量的回归系数分别为0.35、0.33,排名第三的酸碱性的回归系数为0.07,与前面个两个特征相比,该值较小。在实际生产中,为提升白葡萄酒口感,生产商应更多地关注、研究白葡萄酒中的酒精含量和剩余糖分含量。
(4)降低白葡萄酒口感的前三特征为:密度、挥发性酸、氯化物。其中密度的影响最大,为-0.31;挥发性酸的影响第二,为-0.21;氯化物的影响第三,为-0.01。可看到,密度和挥发性酸对降低口感评分的影响较大,氯化物相对较小。在实际生产工艺中,需要更多关注、合理控制白葡萄酒的密度大小与挥发性酸的含量。
(5)在热力图及相关关系计算中,我们得出密度跟剩余糖分(0.84)、酒精(-0.78)的线性相关关系比较强。所以在实际生产中,为了提升口感而不断地提升剩余糖分和酒精含量是不可行的。在提升糖分的同时,要注意密度也有所提升,这时候可适当加入酒精,提高酒精含量来降低密度对口感的影响。应多投入到调配这三个特征的比例,才能更有效地提升白葡萄酒口感,提升销量。
B.下面来看在十折试验中,MSE的一个变化情况:
plt.figure(figsize=(11,9))
plt.plot(Las_cv.alphas_,Las_cv.mse_path_,"-")
plt.plot(Las_cv.alphas_,Las_cv.mse_path_.mean(axis=-1),label="均方误差均值:MSE_mean",linewidth=3,color="b")
plt.axvline(Las_cv.alpha_,linestyle="--",label="10折预测最佳表现对应的alpha值")
plt.xlabel("alpha值",size=16)
plt.xticks(size=16)
plt.ylabel("均方误差(MSE)")
plt.legend(loc="best")
plt.semilogx()
ax = plt.gca()
ax.invert_xaxis()
均方误差随着alpha的减小,渐渐地趋于一定的值,处于基本稳定状态。
print("10折交叉验证中,最佳的惩罚系数:", Las_cv.alpha_)
print("10折交叉验证中,最小的MSE(均值):", min(Las_cv.mse_path_.mean(axis=0))) #均值来的,注意
10折交叉验证中,最佳的惩罚系数: 0.00467052490126
10折交叉验证中,最小的MSE(均值): 0.547575587951
- 在众多的拟合的惩罚系数里,表现最优的惩罚系数为0.0046705249012570426。在这个位置,均方误差MSE基本稳定下来。
- 十折交叉验证里,最小的MSE为0.548.十折的平均值见最粗的蓝色线,在0.73—0.74之间,比对上面的两种方法,效果较好。方程具备现实意义。
C.总的来说:
(1)各特征间存在一定的线性关系,但普遍关系强度不太大;最大的是密度与剩余糖分(0.84)、酒精浓度(-0.78)的线性关系。
(2)找出对白葡萄酒口感影响最大的前三因素:酒精、剩余糖分、密度;
(3)针对给出的11个特征,我们用LassoCV来建模,并给出了最终的模型:
y_scaled = 1.06646156739e-14 + 0.0098704 * x1_scaled - 0.21381849 * x2_scaled + 0.33369253 * x4_scaled -
0.01166061 * x5_scaled + 0.06691956 * x6_scaled - 0.009035 * x7_scaled - 0.31407498 * x8_scaled +
0.07341963 * x9_scaled + 0.06597724 * x10_scaled + 0.352643 * x11_scaled
(4)在实际生产中,厂家应多尝试酒精、剩余糖分、密度的不同比例调配方式。酒精、剩余糖分的含量能提高葡萄酒的口感,而密度大小则会降低酒的口感。另外,要注意到密度跟剩余糖分(0.84)、酒精(-0.78)的相关关系。所以在实际生产中,根据二八定理,针对这三个特征多投入,会得到较大的收益。
3.岭回归:
3.1 部分数据做交叉验证
from sklearn.linear_model import RidgeCV
R1_CV = RidgeCV(cv=10).fit(xx_train, yy_train)
yyR1_pred = R1_CV.predict(xx_test)
print("均方误差:",mean_squared_error(yy_test, yyR1_pred))
Coef3_df = pd.DataFrame(R1_CV.coef_,index=columns[0:11],columns=["回归系数"])
Coef3_df.sort_values(by="回归系数",ascending=False)
均方误差: 0.724085117608
| 回归系数 | |
|---|---|
| 剩余糖分 | 0.436080 |
| 酒精 | 0.309095 |
| 酸碱性 | 0.118767 |
| 游离二氧化硫 | 0.096880 |
| 硫酸盐 | 0.091681 |
| 非挥发性酸 | 0.065386 |
| 柠檬酸 | 0.007297 |
| 氯化物 | -0.003010 |
| 总二氧化硫 | -0.024704 |
| 挥发性酸 | -0.194503 |
| 密度 | -0.454458 |
看到主要影响因素为密度、剩余糖分、酒精、挥发性酸。密度的影响强度最大。下面用全部数据做交叉验证,比对效果。
3.2 全部数据做交叉验证
from sklearn.linear_model import RidgeCV
R2_cv = RidgeCV(alphas=np.arange(0, 100), scoring='neg_mean_squared_error', cv=10).fit(x,y)
print("线性模型的截距:", R2_cv.intercept_)
print("线性模型的回归系数:\n", R2_cv.coef_)
print("最佳惩罚系数:", R2_cv.alpha_)
线性模型的截距: 1.26696321324e-14
线性模型的回归系数:
[ 0.03197363 -0.21165971 0.00223188 0.3755903 -0.01303913 0.0767687
-0.02080385 -0.3747941 0.09182727 0.07351966 0.3229347 ]
最佳惩罚系数: 48
Coef4_df = pd.DataFrame(R2_cv.coef_, index=columns[0:11], columns=["回归系数"])
Coef4_df.sort_values(by="回归系数", ascending=False)
| 回归系数 | |
|---|---|
| 剩余糖分 | 0.375590 |
| 酒精 | 0.322935 |
| 酸碱性 | 0.091827 |
| 游离二氧化硫 | 0.076769 |
| 硫酸盐 | 0.073520 |
| 非挥发性酸 | 0.031974 |
| 柠檬酸 | 0.002232 |
| 氯化物 | -0.013039 |
| 总二氧化硫 | -0.020804 |
| 挥发性酸 | -0.211660 |
| 密度 | -0.374794 |
A.可以看到,基于归一化后的数据:
(1)我们构造的模型为:
y_scaled = 1.26696321324e-14 + 0.03197363 x1_scaled - 0.21165971 x2_scaled + 0.00223188x3_scaled + 0.3755903 x4_scaled - 0.01303913 x5_scaled + 0.0767687 x6_scaled - 0.02080385 x7_scaled - 0.3747941 x8_scaled + 0.09182727 x9_scaled + 0.07351966 x10_scaled + 0.3229347 x11_scaled
(2)剩余糖分、酒精、酸碱性、游离二氧化硫、硫酸盐、非挥发性酸、柠檬酸这7个特征对提升口感评价有正向作用,其影响力依次递减;在一定程度上,这些成分含量越多,口感越好。另一方面,密度、挥发性酸、总二硫化物、氯化物对提升口感有负作用,其影响力依次递减;一定程度上,它们在白葡萄酒里的含量越高,口感越差。
(3)对提升白葡萄酒口感评价影响最大的三个特征为:剩余糖分、酒精含量、酸碱性。剩余糖分、酒精含量含量的回归系数分别为0.38、0.32,排名第三的酸碱性的回归系数为0.09,与前面个两个特征相比,该值较小。在实际生产中,为提升白葡萄酒口感,生产商应更多地关注、研究白葡萄酒中的剩余糖分含量和酒精含量,跟上面LassoCV的结论一致。
(4)降低白葡萄酒口感的前三特征为:密度、挥发性酸、总二氧化硫。其中密度的影响最大,为-0.37;挥发性酸的影响第二,为-0.21;总二氧化硫的影响第三,为-0.02。可看到,密度和挥发性酸对降低口感评分的影响较大,总二氧化硫相对较小。在实际生产工艺中,需要更多关注、合理控制白葡萄酒的密度大小与挥发性酸的含量,与LasscoCV一致。
(5)最佳惩罚系数为48。
三.总结与建议
我们用了一般线性回归、Lasso回归和岭回归,来为白葡萄酒的口感评分建模。模型参见上面结论。
发现:
(1)跟质量评分线性相关程度较强的是:酒精、密度和氯化物,最弱的是柠檬酸。
(2)按正负影响划分因素: 提升质量的因素:酒精、剩余糖分、酸碱性、游离二氧化硫、硫酸盐、非挥发性酸、柠檬酸。 降低质量因素:密度、挥发性酸、氯化物、总二氧化硫。
(3)按影响强度划分因素: 关键影响因素:酒精、剩余糖分、密度、挥发性酸。 次级影响因素:酸碱性、游离二氧化硫、硫酸盐、非挥发性酸、氯化物、总二氧化硫。 最弱影响因素:柠檬酸
(4)为生产质量好的白葡萄酒,生产商应把主要的经历、资金投入到酒精、剩余糖分、密度、挥发性酸这四个主要因素的比例中,提高投入产出比。注意剩余糖分越多,密度同时也增高;而酒精与密度呈负相关关系,可适度多加酒精
(5)在考虑推出新品时,可考虑推出少量极高端、质量一般般的产品,主要推出质量中等、甚至偏上的产品。中等价位的产品更受到消费者青睐。 如果在中等的基础上,对品质提高一个段位,与其他销售产品划开一个层次,可利用价格溢价来提高营收。
(6)做用户分层: 在产品的消费群体中,可针对他们的购买行为(消费时间、消费次数量、消费总金额、消费频次、最近一次消费时间、单次购买金额、单次购买品类等等)作用户分层,分成高中低消费群体,然后针对他们购买的产品、消费的金额、消费的次数来找出这类人群最喜欢什么类型的产品。在后续生产中,可针对不同群体,推出对应的产品。