字符串匹配算法---KMP

在开始正文前先了解两个概念

前缀：

　　除了字符串的最后一个字符外，一个字符串的全部头部组合

后缀：

　　除了字符串的第一个字符外，一个字符串的全部尾部组合

例： 

　　abcd 的全部前缀为： a, ab, abc

　　abcd 的全部后缀为： d, cd, bcd

正文部分：

字符串匹配算法的姊妹篇---BF算法中讲解了如何利用BF算法暴力匹配。

但是在实际执行过程中这种算法却显得很笨重，每一次遇到不匹配的字符时，i与j都要同时回退。

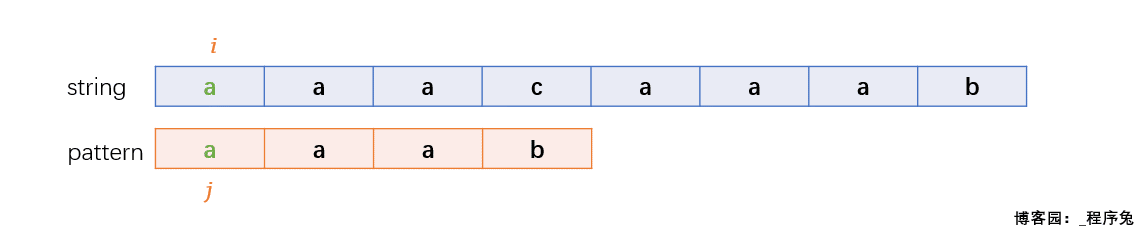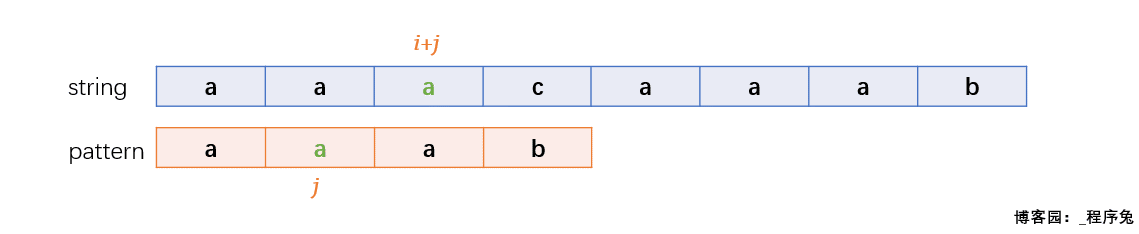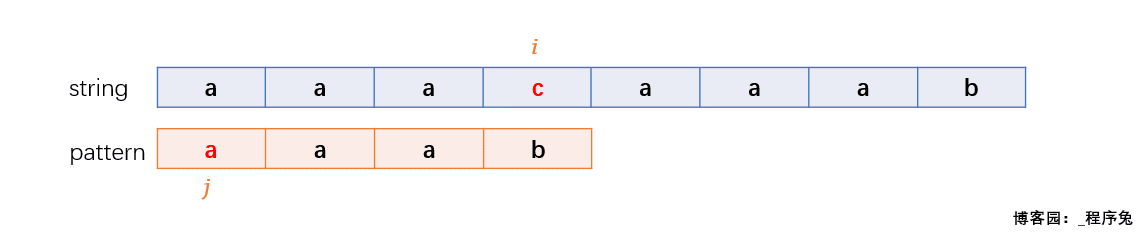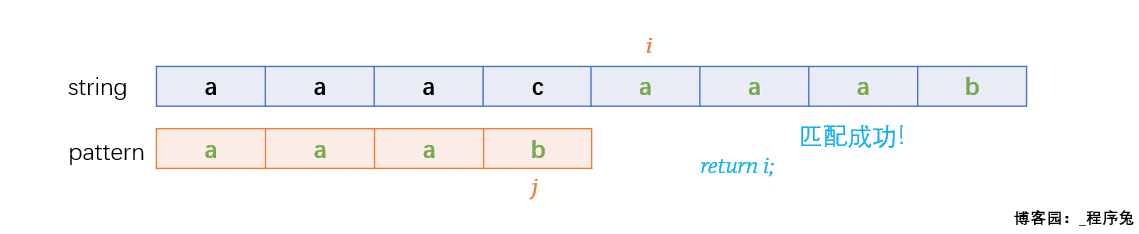
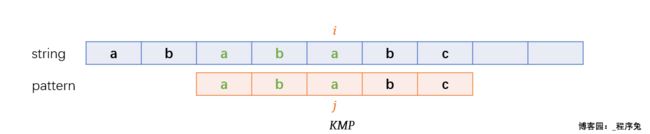
第一次比较到pattern中的b与string中的c时，匹配失败，i和j同时回退，但是很显然，在pattern中并没有字符c，因此我们只需要i移动到c的下一个字符a上，而让j移动到pattern中第一个字符a再次进行匹配。

KMP算法永不回退string的指针i（不重复扫描string），而是借助next数组将pattern指针j移动到正确的位置。

如何找到正确的位置就比较重要，所以先来看个例子思考一下怎样将指针j正确移动以避免重复匹配：

 

当匹配进行到上面这个状态时，前面四个字符均以匹配，到第五个字符 c 与 a 不匹配，这里我们将这种状态称为失配，将string[i]称为失配字符。那么 j 该如何移动才能保证匹配次数尽可能少呢？

经过观察我们发现，pattern中有两个子串很类似，分别是 aba 和 abc ，它们都有共同的前缀ab，唯一区别就是最后一个字符一个为a一个为c；

没错，KMP也发现了这个规律，于是KMP就开始偷懒啦：我现在这个位置若是将j回退到起始位置，有点亏，因为这里有两个前缀相同的子串 aba 和 abc，j当前处于失配字符c，如果我偷个懒只让j回退到aba中最后一个a位置，万一string中失配字符刚好是 a ，那我不就可以继续匹配了。

 

 

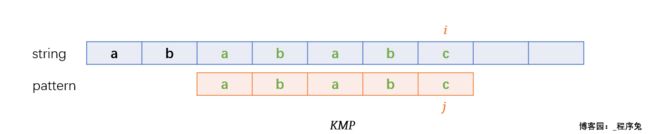
 于是就产生了下面的移动， j 移动到 pattern[2]，i 依旧指向失配字符 a ， 哇，移动之后，太巧了吧，刚好匹配！KMP：还好没有全部回退，我可真是个机灵鬼。

 

 

 OK，继续干活

 

 

 匹配成功！

在上面这个例子中当匹配到字符 c 时，发生了失配现象，这个时候 KMP 的做法并不是像BF那样笨笨的将 j 全部回退 ，i + 1，然后重新从 i 开始一个个的与 j 匹配。而是 找到了aba 和 abc这两个有公共前缀的子串，并让 j 移动到了 aba中最后一个a 位置（与abc中c等价的位置），然后继续将失配字符与 指针 j 字符进行匹配。

在上面这个过程中，pattern为 ababc，当 j 从 0 开始遍历时，遍历过的字符都会组成pattern的一个个子串。

例如：当 j = 0 时，当前子串为 a

　　   当 j = 1时，当前子串为 ab

          ....

          当 j = 4时，当前子串为 ababc

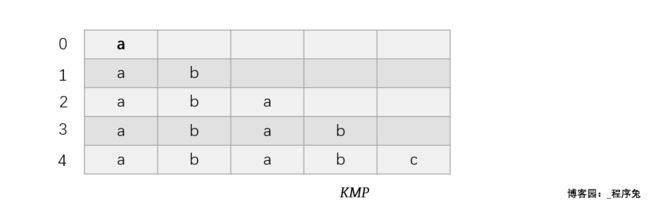
先列出 j 从 0 到 strlen(pattern)的所有经过的子串

 

 

 当 pattern[j] = 'c' 时，当前子串为 ababc，那么就有两种情况：字符'c'匹配成功 或 字符 'c' 失配（事实上，当 j 遍历 pattern中任意一个字符时，都会产生这两种情况，失配或匹配）；匹配成功 i++, j++；这里主要考虑失配后 j 的去向。

本例中，字符 'c' 失配，j 由4变为了 2，如果将pattern中 j 遍历到每一个字符失配后 j 的去向用一个数组存储就产生了next。很显然这里，next[4] = 2，即失配后执行的操作为  j = next[j];（j = 4时，若pattern[j]失配则 j 移动到 2 继续匹配）

假设我们已经求得了next数组，知道 j 每一步失配后应该去哪里，那么我们就产生了如下代码：

int KMP(char pattern[], char str[]) // pattern 为模式串  str为待搜索string串
{
    int *next = next_arr(pattern);  // next_arr 为 获取 next数组函数；int i = 0; 
    int j = 0; // 从第一个字符开始比较
    while(str[i]){
        if(j == -1 || str[i] == pattern[j]){ // 从头重新匹配 或 匹配成功
            ++i;++j;
        }else{  // 失配
            j = next[j]; 
        }
        if(j == strlen(pattern)){ // 判断是否全部匹配正确
            return i - j;  // 匹配正确返回 str 串中起始index
        }
    }
    return -1; // 匹配失败
}

还有一个问题是：next数组如何产生？

还记得在例子中我们提到的 有公共前缀 ab 的两个子串 aba 和 abc 吗？

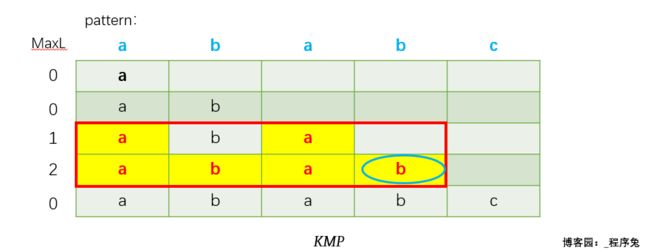
当前 j = 4，形成子串为 ababc，字符'c'失配。我们说这里发现了 “公共前缀”ab，那这个ab是怎么得来的？在没有任何知识储备之前，我是拿眼睛看出来的。

在有了知识储备之后，ab在abab（注意是abab而不是ababc）这个子串中被称作前缀后缀公共元素，其长度被称为前缀后缀公共元素的最大长度。什么意思呢？

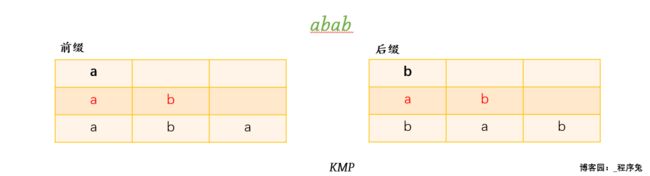
让我们先列出abab的所有前缀和后缀。

 

 

 将前缀后缀一一对比，发现 ab 为前缀后缀公共元素，其长度为2，其余一个元素的前后缀与三个元素的前后缀均不相等。

因此我们例子中瞎编的名词 “公共前缀”ab 就是这么得来的。

那得出这个 ab 有什么用呢？而且这个 ab 是在子串 abab中得来的，和 已经遍历到 字符 'c'的子串 ababc 又有什么关系呢？

为了简洁起见，我们将 abab 这个子串中前缀ab 简称 p-ab，后缀 ab 简称 s-ab。

无论 s-ab的下一个字符是什么，只要失配则 j 需要回退，此时 j 仅仅只需要回退到 p-ab的下一个字符 a 即可，因为 p-ab 与 s-ab完全相同。

因此在 遍历至子串 ababc 时， j 的回退位置(  next[j]  )实际是 它的前一个子串abab产生的前后缀公共元素最大长度的值。

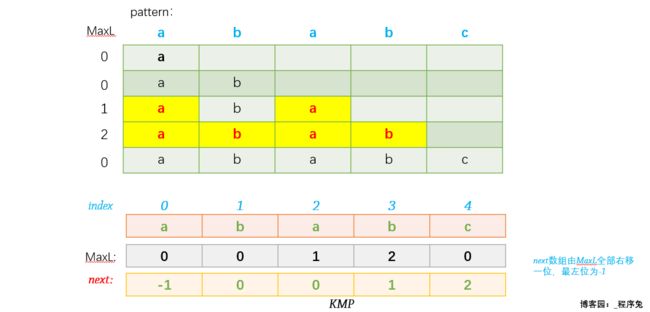
故 想要知道当 j 遍历到每一个pattern元素时失配后如何回退就必须得到 next 数组的值，因此就必须对 pattern 的每个子串求其前后缀公共元素最大长度，记为 MaxL; 

next 数组的值即是 MaxL 数组整体向右移动一位，最左边next[0] 为 -1。

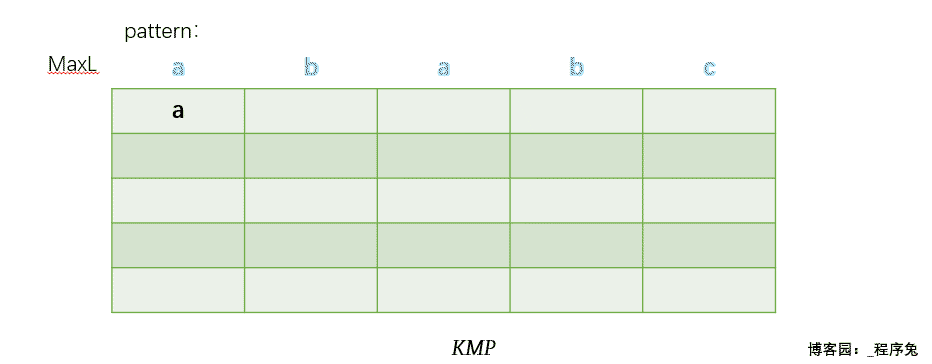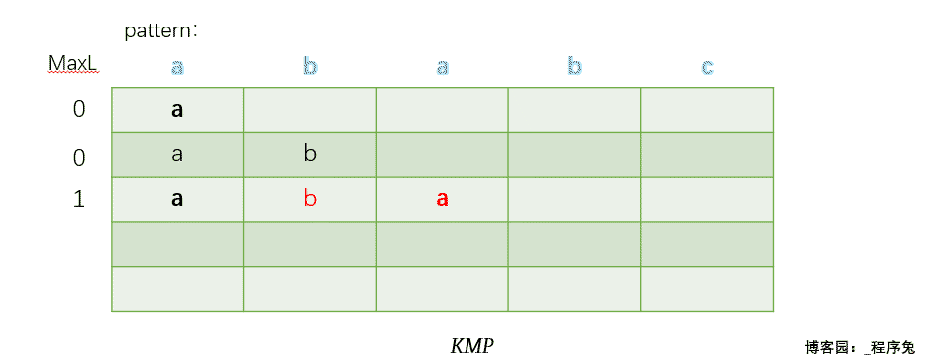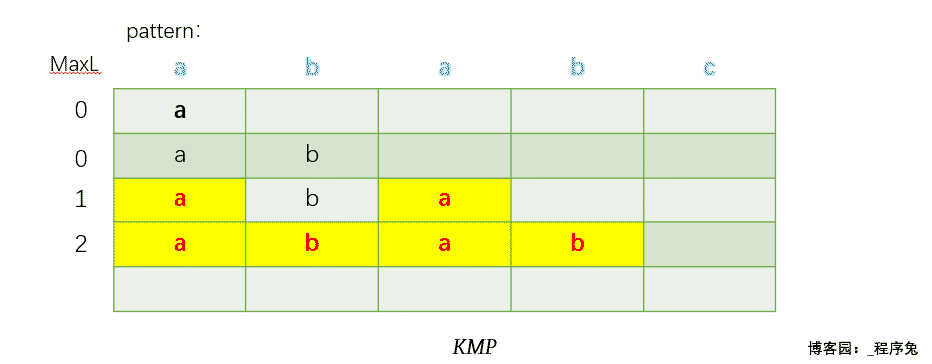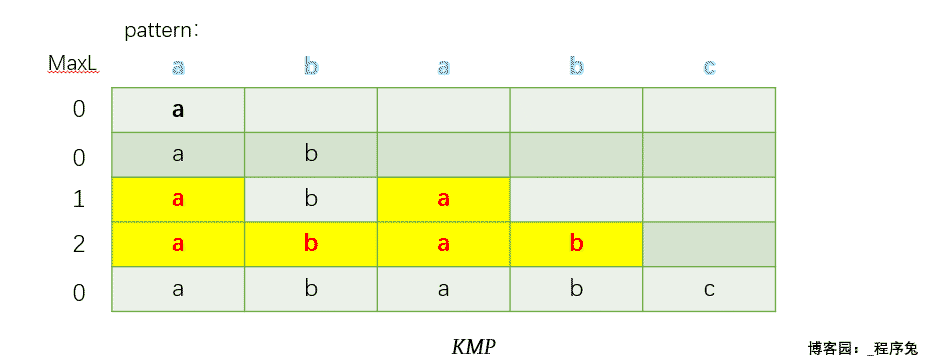
给出一张动态图感受一下MaxL以及前后缀公共元素的求解过程。（每一行代表一个子串，最左边一列为该行子串对应的前后缀公共元素最大长度，最终用黄色标注出的部分为前后缀公共元素）

 

 

 

 

  这样我们就成功得出了next数组。其代码实现有两种方式，一种是直接求取，一种是递推求取。

1.直接求取

  伪码描述

int *next_arr(char pattern[])
{
    int len = strlen(pattern);
    int *next = new int[len];
    // next数组为 MaxL元素右移一位,next[0] = -1
    // 因此next数组 next[i]的值为/***当前子串的前一个子串***/的前后缀公共元素最大长度
    for(int j = 0; j < len; ++j){ 
        // j 遍历pattern，j处当前子串pattern[0...j]长度为 j+1
        //                j处前一个子串pattern[0...j-1]长度为 j
        //                j处前一个子串的最长前后缀长度为 j-1
        // j == 0, next[j] = -1
        // j == 1, 当前子串长度2,前一个子串长度1，无前后缀，next[j] = 0
        // j > 1
        　　int p; // p动态表示前后缀长度 
        　　// p由最大开始递减（最短前后缀1 <= p <= 最长前后缀 j-1），
        　　//      直到前后缀相等break跳出循环，所得长度即是pattern[0...j-1]的前后缀公共元素最大长度
        　　for(p = j-1; p > 0; --p){ 
          　　  // 前后缀相等break退出循环
        　　}
        　　// 若 p == 0，则没有发现前后缀公共元素，next[j] = 0 
    }
    return next;
}

代码实现

bool IsEqual(char*,int,int);
int *next_arr(char pattern[])
{
    int len = strlen(pattern);
    int *next = new int[len];
    for(int j = 0; j < len; ++j){ // j标识当前子串，j值为前一个子串长度
        if(j == 0){  // next[0] = -1
            next[j] = -1;
        }else if(j == 1){ // 一个元素的子串无前后缀
            next[j] = 0; 
        }else{
            int p;
            for(p = j-1; p > 0; --p){ // p 标定所求子串前后缀长度，从最长j-1 开始递减至 最短1
                if(IsEqual(pattern, p, j)){ // IsEqual判断前缀pattern[0...p-1]后缀pattern[j-p,j-1]是否相等
                    next[j] = p;
                    break;
                }
            }
            if(p == 0){ // 当前子串没有前后缀公共元素
                next[j] = 0;
            }
        }
    }
    return next;
}

bool IsEqual(char pattern[], int ps_len, int subPattern)
{
    // ps_len为前后缀长度，subPattern为子串长度
    // 判断从 pattern[0...ps_len-1] 及 pattern[subPattern-ps_len...subPattern-1]的串是否相等
    for(int i = 0; i < ps_len; ++i){
        if(pattern[i] != pattern[subPattern - ps_len + i]){
            return false;
        }
    }
    return true;
}

直接求取模仿了依次从子串中求取前后缀公共元素的过程，时间复杂度较高

递推求取则利用了一定的规律

2.递推求取

先看一下为什么可以采用递推求取

 

 

 

 容易发现，在求取aba子串和abab子串的MaxL值时，abab这个子串就做的很不聪明，很明显，abab这个子串比aba子串刚好多出一个 b，这就让abab中恰好有一个p-ab和一个s-ab，MaxL值为2，如果不利用这个可能出现的巧合，那么就只能将abab子串的所有前后缀列出一一比较求取，是不是很浪费时间。

 由于这是个递推，代码行数很少光看代码不是很容易理解，所以我准备将整个过程过一遍方便理解：

先看一遍代码

int *next_arr(char pattern[])
{
    int *next = new int[strlen(pattern)];
    int i = 0;
    int j = -1;
    next[0] = -1;
    while(i < strlen(pattern)-1){
        if(j == -1 || pattern[i] == pattern[j]){
            ++i;
            ++j;
            next[i] = j;
        }else{
            j = next[j];
        }
    }
    return next;
}

动态图演示

 

 

 

解释：

　　next[0] = -1；

　　假设next[i] = j;  则  pattern[0...j-1] == pattern[i-j...i-1];

　　　　此时若 pattern[j] == pattern[i] ， 则 pattern[0...j] == pattern[i-j, i];  即 next[i+1] == j+1

　　　　若  pattern[j] != pattern[i] ，发生失配，此时只需要将 j 移动到正确的位置继续判断。即 j = next[j]; （这一部分思想与我们前面讲过的在 string中 匹配 pattern串相似，str[i] != pattern[j]即失配， j = next[j] 继续匹配）