【数据结构】02 字符串匹配&KMP算法
字符串匹配
有如下两个字符串S和P,需要判断出P是否为S的子串。

简单的方法是以S的每个字符为匹配串的首个字符,将其与P串进行匹配。这个算法的时间复杂度为O(mn),若遇到较大的字符串,耗时长。
实现方法如下:
//传入s起始
bool comparep_s(int j, char* p, char* s)
{
int k = 0;
while (s[k] != '\0') {
if (s[j + k] != p[k]) {
return false;
}
k++;
}
return true;
}
int comparechar(char* p, char* s) {
int i = 0;
int slen = strlen(s);
for (i = 0; i < slen; i++) {
//s[i]开始的长为plen的字符串与p匹配是否成功
if (comparep_s(i, p, s) == true) {
return i;
}
}
return -1;
}
int main() {
char s1[] = "actgpactgkactgpacy";
char s2[] = "actgpacy";
int result = comparechar(s2, s1);
printf("result: %d\n", result);
}
KMP算法
分析
我们发现,事实上,通过第一轮匹配,我们可以知道S的前长度为P的字符串的内容,这时候我们需要考虑下一轮匹配时从S的字符串的哪个地方开始匹配子串。这时候可能会想到,是不是在上一轮S匹配的末尾开始进行新一轮的全面比较就可以了呢?但是,我们可能会忽略掉在上一轮终止位置的前面可能存在正确的字符匹配这种情况。那如何能让S的指针不回溯呢?
我们会很容易看到,如下图所示的地方j是S字串在上一次匹配后,P的首字符A首次出现的位置,我们这时只需要从A这个地方,以A为首个匹配字符开始比较。此外,还可以注意到,是不是能够依旧之前扫描过的后几位来帮助我们匹配新字符串除了首字符A之外的字符与P的其余字符的匹配程度。即j处所指向的A->C 与 P首字符的A->C相匹配。那么在下一次匹配时,我们就只用从P的T位置与S的上一次比较位开始匹配,这些特点都是由第一次匹配就可以得到的。故而,我们要想保持S的指针j不回溯,需要记录在前面查询过的字符串中是否会存在能把S匹配首字符提前的情况,我们只用记录下一次匹配时P要匹配的初始位置即可。由此,产生了KMP算法。
KMP算法

KMP算法设置了两个指针,指针i指向P的下一轮应该开始匹配的位置,指针j指向S的比较位。具体表现如下:
当我们第一次比较时,i,j的指向情况如下图所示:

我们发现P的前2个字符AC在S已比较的字符中二次出现了,这时,保持j不变,只用将指针i拨回到下方位置即可开始下一轮比较。

接下来进行正常比较,i++,j++,比较到这个地方发现不匹配。

在这里,回看前面S已经比较过的字符串,不存在有与P的前几个字符一致但没经比较的的字符,所以j往后走可以正常的与P的整个字符串相比较,即要把整个P与S从j开始的字符串相比较,i=0。
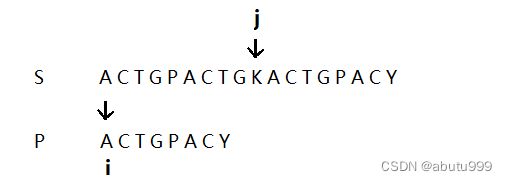
这时比较,发现首字符都不匹配,j++,直到j的位置指向A,这时再继续字符串的匹配。

这时,进行新一轮的匹配,发现匹配成功!
在这个过程中,我们并没有将j做回溯,但是需要把i做回溯,至于i应该回到哪个地方,我们使用next数组进行决定。
next数组大小与子串P的大小一致,next[0,1,…,n-1],next[i]取值为P[0,1,…,i-1]的的最长公共前缀后缀长度。
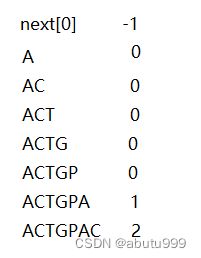
对于P串:ACTGPACY
规定next[0]=-1。
则next=[-1,0,0,0,0,0,1,2]
代码实现
算法构造:
- 计算字串P的next数组
- 遍历主串S,j++,直到S[j]=‘\0’
- 开始字符串匹配:每次字符串匹配后,返回匹配结果:i下一轮应该所指向的位置以及是否匹配成功。若未匹配成功,且S[j]!=P[i],j++,直到S[j]==P[i]。此时开始下一次的匹配。一直到匹配成功。
匹配函数:传入S,P,以及i,j
next数组
对于字符串 abcba:
前缀:它的前缀包括:a, ab, abc, abcb,不包括本身;
后缀:它的后缀包括:bcba, cba, ba, a,不包括本身;
最长公共前缀后缀:abcba 的前缀和后缀中只有 a 是公共部分,字符串 a 的长度为 1。
现在已知字符串abcabdd,next[0]=-1,next[1]=0。
如何从next[i]求取next[i+1]
next[1] = 0, next[2] ?
设置指针j,表示相同字符串的匹配终止位置。
已知当next [i= 1] 时,截取的字符串a, j =0, 指向首字符a, 表示没有公共前后缀。
下一次next[ i+1 = 2]时 , i指向c, p[i-1] !=p[j], 此时j=0,前方没有公共部分,next[i] =0;
下一次next[i=3],i指向a, p[i-1] !=p[j], 此时j=0,前方没有公共部分,next[i] =0;
下一次next[i=4],i指向b, p[i-1] =p[j],表示有一个字符匹配上了,next[i] ++; j++;
下一次next[i=5],i指向d, p[i-1] =p[j],表示有一个字符匹配上了,next[i] ++; j++;
下一次next[i=6],i指向d, p[i-1] !=p[j],表示字符没有匹配上了,查看j=2不为0,说明起始有2个字符时匹配的,将j = next[j],得到j=0; 查看此时,p[i-1] !=p[j],表示字符没有匹配上,又j=0,所以next[i]=0;
综上:
- 初始化next[0] = -1, next[1] =0; i =2; j =0;
- while i < len ( p ):
- if(p[i-1] == p [j]) do : next[i]++; i++; j++;
- else if( j =0) do: next[i] = 0; i++
- else do: j=next[j];
int* renext(char* p) {
int plen = strlen(p);
int* next = (int*)malloc(sizeof(int) * plen);
next[0] = -1;
next[1] = 0;
int i = 2, j=0;
while (i < plen) {
if (p[i - 1] == p[j]) {
next[i] = j+1;
i++;
j++;
}
else if (j > 0) {
j = next[j];
}
else {
next[i] = 0;
i++;
}
//printf("next[%d] : %d\n", i-1, next[i-1]);
}
return next;
}
KMP算法主体
bool comparekmp(int* next, int *i, int *j, char* p, char* s) {
while (p[*i] != '\0') {
if (p[*i] != s[*j]) {
break;
}
(*i)++;
(*j)++;
}
printf("i: %d, j: %d\n", *i, *j);
if (*i == strlen(p)) {
return true;
}
*i = next[*i];
printf("i: %d\n", *i);
return false;
}
int kmp(char* p, char* s) {
int* next = renext(p);
int j=0;
int i = 0;
while (s[j] != '\0') {
printf("比较后:\n");
bool flag = comparekmp(next, &i, &j, p, s);
printf("flag: %d\n", flag);
if (flag == 1) {
return j-strlen(p);
}
else{
if(i==-1){i++;j++;}
while (p[i] != s[j] && j<strlen(s)) {
j++;
}
}
printf("i: %d, j: %d\n",i, j);
}
return -1;
}
官方解答:
int* renext0(char* needle) {
int nlen = strlen(needle);
int* next = (int*)malloc(sizeof(int) * nlen);
next[0] = -1;
if(plen > 1){
next[1] = 0;
}
int i = 2;
int j = 0;
while (i < nlen) {
if (needle[i - 1] == needle[j]) {
next[i] = j + 1;
j++;
i++;
}
else if (j == 0) {
next[i] = 0;
i++;
}
else {
j = next[j];
}
}
return next;
}
int strStr0(char* haystack, char* needle) {
int* next = renext0(needle);
int hlen = strlen(haystack);
int nlen = strlen(needle);
int j = 0, i = 0;
while (j < hlen && i < nlen) {
if (i == -1 || haystack[j] == needle[i]) {
i++;
j++;
}
else {
i = next[i];
}
}
if (i == nlen) {
return j - i;
}
else {
return -1;
}
}