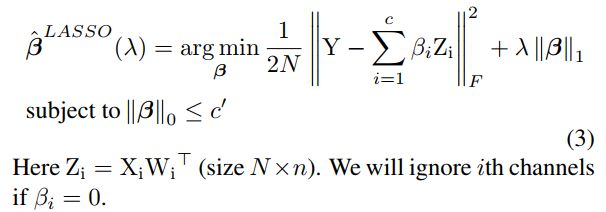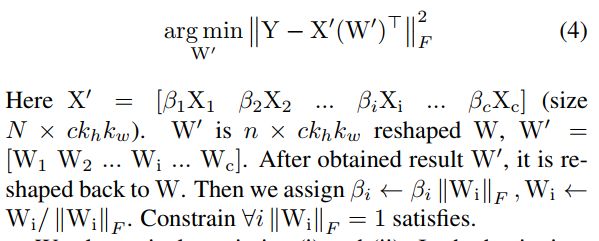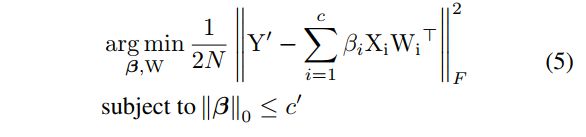CNN推理优化系列之三：Channel pruning

介绍

曾在‘CNN推理优化系列之一: Filter pruning’中讲过filter pruning在CNN inference时的优化。此篇同样也是致力于减少layer计算的channels数量，但其思路又与上篇文章不同。

单独考虑一个conv层的计算，即可以想着将它weight tensor里面的某些权重较轻的（L1-norm值较小）filters去掉以节省计算，也可以考虑减少输入feature maps中的若干channels信息，
然后通过调整weights使整体output feature map的信息不会丢失太多。本篇即是后一种思路。

Channel_pruning方法

Channel pruning方法

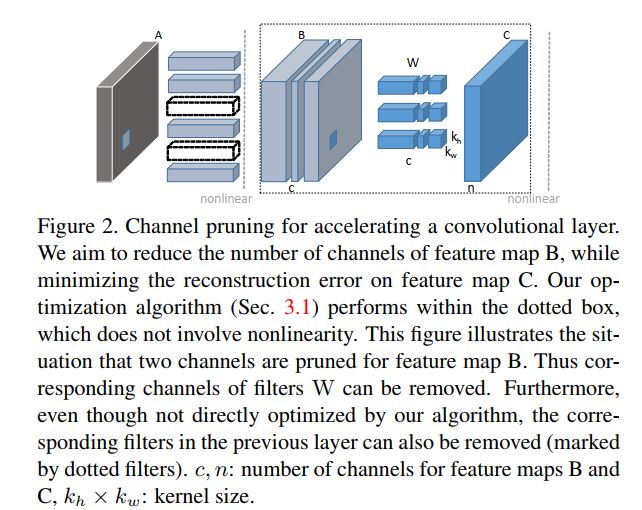
假设我们想试着减少某一单独conv层的计算。已知它的如下信息：

• Input feature map X的shape: N x c x IH X IW，其中N 为batch size，c为输入feature map数目，IH与IW分别为输入feature map的长与宽；
• convolutional filters W的shape: n x c x K_h x K_w，其中n与c分别为此conv层输入、输出feature map channels数目，K_h与K_w则为conv kernel的长与宽；
• Output feature map Y的shape: N X n x OH X OW，其中N为batch size，n为输入feature map数目，OH与OW分别为输出feature map的长与宽。

本文中，我们要解决的问题是如何在减少X某些channel信息的同时，保证Y的整体信息仍然不会损失太多。以下公式可表示此一优化问题。

整体优化问题

在此一l₀优化问题中，我们共有两个矢量参数需要求解，其一为β，它决定了我们从c个输入channels中选择啥些input channels，进而舍弃哪些。若β_i = 0，则第i
个channel将被舍弃，反之若β=1，则第i个input channel feature map信息将被保留。另外一个需要考虑的参数则是W（Conv weights），显然那些被舍掉的weight信息，我们
不需要再保留了，但不仅于此，我们还要考虑调整W的值使得选择后的减少的input feature map组合经过conv filter处理后依然得到与之前输出Y近似的信息即Y^'。

Channel pruning方法的分步骤施行

原始优化问题的放松变形

上述讨论过的l₀优化问题本质上是个NP-hard问题。我们给其多些约束，进而将它变为如下所示的l₁ norm优化问题。

Channel_pruning优化问题的放松变形

首先增加了参数β的normalization factor，从而让它向着我们关心的方向寻找合适的参数集合（即让β有尽量多的0，从而pruning掉一定的input channels信息）。
另外则增加了W的范数为1的强约束以让我们得到的W解不过于简单（这一点不太理解）。

进而我们再将它变为两个分步骤的子优化问题，分别由以下两小节内容来概述。

求参数β的子优化问题

首先，我们可固定W不变，寻求参数β的组合，即决定输入feature map的哪些input channels可以舍弃。这显然是个NP-hard的组合优化问题，作者使用了经典的启发式LASSO方式来
迭代寻找最优的β值，如下公式所示。

子优化问题其一

求参数W的子优化问题

然后我们再固定上面得到的β不变，再求解最优的W参数值，本质上就是求解如下的MSE问题。

子优化问题之二

整体求解方案

上面三小节中讲了使用channel pruning方法的理论方法。在实际操作时有如下两种可循的途径。

其一：交替着优化问题一与二，即最开始的时候用trained model weights来初始化W值，并设λ为0，即不设任何normalization penality factor，而||β||则为c，即保留所有的
input channels信息；然后随着迭代进行，逐渐增加λ的值；而每改变一次λ值，我们将会一直交替优化求解β与W，直至最终||β||稳定下来。等到最终||β||的值满足小
于或等于c^'的要求时，就停下来，然后就得到最终的W值为{β_iW_i}。

其二：分别进行两个优化问题。即先持续优化得到β值，使其满足||β|| <= c^'，然后再固定β，优化一次得到W值。

作者观察表明此两种方法的效果近似，而第二种计算量显然更小，更合乎实际，因此最终为本文大多实验所采用。

整个model的pruning

以上所介绍的方法为单个conv层pruning所使用的方法。而在将此方法应用于整个CNN model时，方法也类似，只需要sequentially将此它应用于每个层即可（当然某些特殊的多分支层需要稍稍特殊对待）。
以下为用于整个model时每个层所应用的优化pruning。

整个model的pruning

与公式一相比，它使用Y^'替换掉了Y，这里Y^'指的是原始model上的输出feature map，因此我们会在整个model weigth参数调整时考虑accumulated error的影响。

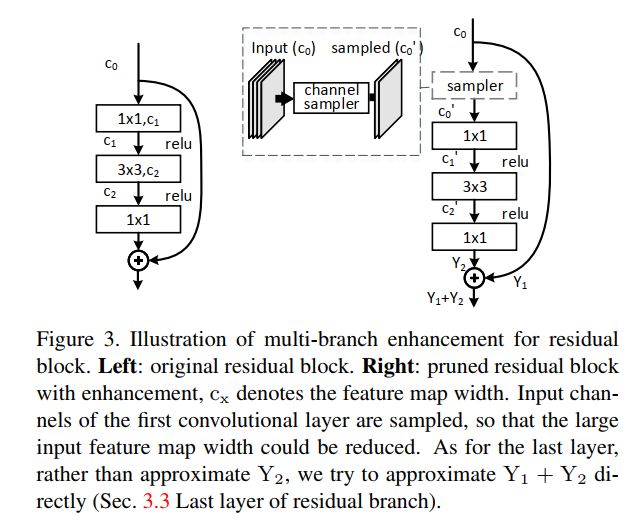
Multi-branch networks pruning

同之前讲过的filter pruning一样，channel pruning同样要考虑像Residual module那样multi-branch的情况。

Residual_modeul上面的channel_pruning

这里考虑一个典型的Resudal module的channel pruning的方法。显然中间的3x3 conv可以像正常的single branch conv上介绍的方法进行优化。
而第一个1x1 conv (bottleneck)以及第二个1x1 conv(expanding module)，则需要另外考虑。

Last layer的pruning

对于最后一个1x1 conv的pruning，我们不仅要考虑residual分支上的信息恢复，同样要考虑到identity maping分支上面的信息丢失。因此最终用于恢复的目标值并非是Y₂，而是Y₁ - Y'₁ + Y₂。
这样就可以在W的计算中考虑进去identity maping上信息的恢复了。

first layer的pruning

同样对于第一个1x1 conv，我们对input feature maps也不能妄加pruning，毕竟它是与identity maping分支共享input feature maps的。为了不对identity maping分支有影响，在这里加入了一个sampler op用于
从输入的feature maps上进行特征提取，这样就能将第一个1x1 conv变成一个正常的conv层了。

实验结果

以下为channel pruning方法在单个层pruning上与我们之前讲过的filter pruning方法的比较。看得出它的结果是要好上一些。毕竟在此方法里，我们真正会pruning掉的是那些inter-input-feature maps之间的冗余信息。

单个层pruning结果比较

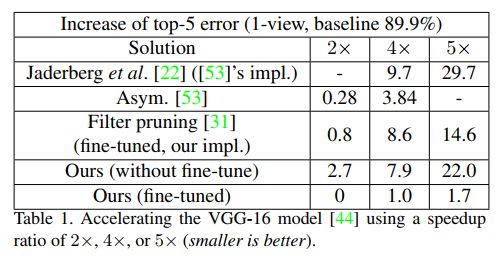
以下为在获得相同加速比的时候，channel pruning方法与其它inference加速方法在VGG loss上的损失比较。

Channel_pruning方法与其它加速方法在整个model_loss上的比较

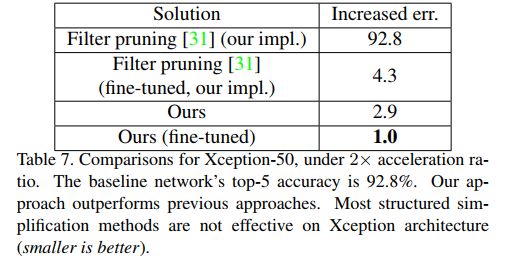
以下为在Xception上面的结果比较。

Xception上的结果比较

参考文献

• Channel Pruning for Accelerating Very Deep Neural Networks, Yihui-He, 2017