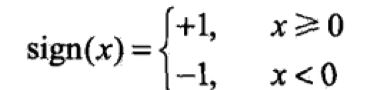【概述】
1、感知机模型特征:感知机对应于输入空间中将实例划分为正负两类的分离超平面,属于判别模型。
2、感知机策略:感知机学习的目标是求出将训练数据进行线性划分的分离超平面,导入基于误分类的损失函数,利用梯度下降法对损失函数进行最小化,求得感知机模型。
3、感知机学习算法:用学习得到的感知机模型对新的输入实例进行分类。
4、重点:感知机是神经网络和支持向量机的基础,所以一些核心概念要仔细理解和和掌握。
一、感知机模型(机器学习三要素之一)
1、定义2.1(感知机)
公式说明:W和b为感知机模型参数,称为权值(weight)或权值向量(weight vector),b称为偏置,一般b会以bx0的方式形成统一的权值向量w,w.x表示w和x的内积(内积的定义见附录1),sign(x)是符号函数,即:
图2.1:Sign符号函数的几何表示
2、感知机的几何解释
线性方程w.x+b=0对应于特征空间的一个超平面S,其中w是超平面的法向量(法向量和超平面的关系见附录2),b是超平面的截距。
该超平面将特征空间划分成两个部分,位于两部分的点(特征向量)分别被分成正、负两类,超平面S成为分离超平面。
3、感知机学习方法
由训练集(实例的特征向量及类别)T= {(x1,y1),(x2,y2),…,(xn,yn)},通过学习求得感知机模型(2.1),即求得模型参数w。
4、感知机应用举例(贷款申请)
每个申请贷款的人者有若干特征,包括年龄、性别、收入、负债情况,上述这些特征构成特征向量x(x1,x2,...xn)。《统计学习方法》中图2.1给出的是x的二维向量实例,在图2.1中,超平面简化为斜率为-w1/w2的分类直线。
申请者的数据,通过w加权取得总分,减去这个门槛值,总分超过门槛值(即大于等于0)就给+1,没超过(即小于0)就给-1 (另一个例子是“学生是否及格的判断”)
二、感知机学习策略(机器学习三要素之二)
1、数据集的线性可分性
如果存在某个超平面S,能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧,即对所有yi=+1的实例1,有w.xi+b>0;对所有yi=-1的实例i,有w.xi+b<0,则称数据集T为线性可分数据集。
否则,则称数据集T线性不可分。
注:从上文可看出:
1)如果找到合适的超平面,正确划分好的两个区域或空间中,yi和w.xi+b为同符号,同为正值或同为负值,即yi.(w.xi+b)>0;
2)对于没有完全正确区分的超平面,存在yi.(w.xi+b)<0的xi误分类点;
3)感知机的优化就是通过对xi误分类点到待优化超平面S的距离进行最小化调整。
2、感知机学习策略
为了找出这样的超平面,需要确定学习策略,定义(经验)损失函数并将损失函数最小化。
在此选取“误分类点到超平面S的总距离”作为损失函数。
首先写出输入空间R任一点x0到超平面S的距离(注:点到直线/平面的距离计算见附录3):
(基于符号函数中的yi特性)对于误分类的数据(xi,yi)来说,-yi(w.xi+b)>0成立。
因此,假设超平面S的误分类点集合为M,所有误分类点到超平面S的总距离为:
感知机损失函数的定义:
【小结】感知机学习的策略,就是在假设空间中选取使损失函数(2.4)最小的模型参数w,b,即感知机模型。
三、感知机学习算法(机器学习三要素之三)
感知机学习问题转化为求解损失函数(式2.4)的最优化问题(最小值min),最优化的方法是随机梯度下降法(Stochastic gradient descent)。
感知机学习算法是误分类点驱动的(注:这个在林轩田的视频中也反复提到,戏称“有错能改”算法)。
本节介绍具体算法,包括原始形式和对偶形式,并证明在训练数据线性可分条件下学习算法得收敛性(有限次数的优化步骤)。
1、感知机学习算法的原始形式
1)算法思路
采用误分类驱动方式,当一个实例点被误分类,即位于分类超平面的错误一侧是,则进行w、b值的调整,使分离超平面向该误分类点的一侧移动,以减少该误分类点跟超平面的距离,直到超平面越过该误分类点使其被正确分类。
2)梯度的计算方式,
采用偏导数方式,分别对L求变量w和变量b的偏导,计算损失函数L(w,b)的梯度。具体如下:
∇wL(w,b)=-∑yi.xi
∇bL(w,b)=-∑yi
上述就是,求得w和b的变化梯度,分别是yixi和yi
普遍性地,随机选取一个误分类点(xi,yi),对w和b进行更新
w<—w+ηyixi
b<—b+ηyi
这里,η是自变量的步长,统计学习中又称为学习率(learning rate)。
通过迭代可以期待损失函数L(w,b)不断减少,直到为0。
3)感知机学习算法的原始形式
通过上述分析,得到以下算法(算法2.1)
(1)输入:
训练集T={(x1,y1),(x2,y2),(x3,y3),...,(xn,yn)},其中xi∈X=Rn,yi∈Y={-1,1},i=1,2,...,N;学习率η(0<η≤1);
(2)输出:
w,b;感知机模型f(x)=sign(w.x+b)
第1步:选取初值w0、b0
第2步:在训练集中选取数据(xi,yi)
第3步:如果y(w.xi+b)≤0,则进行以下迭代
w<— w+ηyixi
b<— w+ηyi
(4)更新w值和b值,转到第(2)步,直到训练集中没有误分类点
注:算法2.1体现了误分类驱动
2、感知机学习算法的对偶形式
思路:将w和b表示为实例xi和Label标记yi的线性组合的形式,并通过求解系数求得w和b。
(1)在算法2.1中可假设初始值w0、b0均为0,对误分类点(xi,yi)通过
w<— w+ηyixi
b<— w+ηyi
(2)逐步修改w、b,假设修改n次,则w,b系数关于(xi,yi)的增量分别就是aiyixi和aiyi,这里ai=niη。
这样,从学习过程可以看出,最后学习到的w,b可以分别表示为
w=∑(I=1,N)aiyixi
b=∑(I=1,N)aiyi
通过上述分析,得到以下算法(算法2.2)
1)输入
训练集T={(x1,y1),(x2,y2),(x3,y3),...,(xn,yn)},其中xi∈X=Rn,yi∈Y={-1,1},i=1,2,...,N;学习率η(0<η≤1);
2)输出
a,b;感知机模型f(x)=yi(∑(j=1,N)ajyjxj.xi+b)≤0
其中,a=(a1,a2,...,aN)T
(1)a<—0,b<—0
(2)在训练集选取数据(xi,yi)
(3)如果yi(∑(j=1,N)ajyjxj.xi+b)≤0
ai<—ai+η
b<—b+ηyi
(4)更新a值和b值,转到第(2)步,直到训练集中没有误分类数据
例题2.2:正样本点是x1=(3,3)T,x2=(4,3)T,负样板点是x3=(1,1)T,以下试用感知机学习算法对偶形式求感知机模型
解:
按照算法2.2
1)取ai=0,i=1,2,3,b=0,步长η=1
2)计算Gram矩阵
目前训练集中有3个实例(3个样本,2个正样本,1个负样本),分别是a1=(3,3),a2=(4,3),a3=(1,1)三个向量
注2:3个实例形成一个Gram矩阵如下:
[A11,A12,A13
A21,A22,A23
A31,A32,A33]
行一列一元素A11=
行二列三元素A13=
行二列二元素A22=
行三列一元素A31的内积=3*1+3*1=6;行三列二元素A32的内积=4*1+3*1=7
行三列三元素A33的内积=1*1+1*1=2。
推出对应的Gram矩阵如下:
[18,21,6
21,25,7
6,7,2]
3)误分条件
yi(∑(j=1,N)ajyjxj.xi+b)≤0
参数更新
ai<--ai+1
b<--b+yi
4)迭代,形成以下表格
5)最后形成分离超平面(本章是线性分离直线)
w=2x1+0x2-5x3=(1,1)T(T是转置)
b=-3
x1+x2-3=0
W的系数都是1
6)得出感知机模型
f(x)=sign(x(1)+x(2)-3)
附录1 :关于内积的定义
两个向量的内积等于一个向量的模跟另一个向量在这个向量的方向上的正投影的数量的乘积。
内积的用途是判断两个向量的相似度:两个向量是否接近或相等,判断就是这两个向量的内积最大化
附录2:关于法向量的概念
空间直线L.Ax+By+Cz+D=0的法向量的法向量是(A,B,C)
证明:直线斜率是-A/B,向量斜率是B/A,斜率乘积是-1,所以Ax+By+Cz+D=0与向量(A,B,C,)垂直
附录3:关于点到平面的距离计算方式
附录4:为何感知机不能区分XOR函数