本章涉及知识点
1、数据场景
2、模型选择
3、数据探索
3.1、正负样本的占比
3.2、缺省值检测
3.3、单一特征在所有类别中的分布
3.4、每个特征在所有类别中的分布
3.5、彼此特征之间的相关性矩阵
3.6、高维特征空间在低维空间的分布
4、特征工程
4.1、特征标准化
4.2、特征选择
4.3、数据降维
5、模型训练和评估
5.1、处理训练集样本不平衡
5.2、训练模型
5.3、评估模型:混淆矩阵
6、模型调优
7、结果分析
一、数据场景
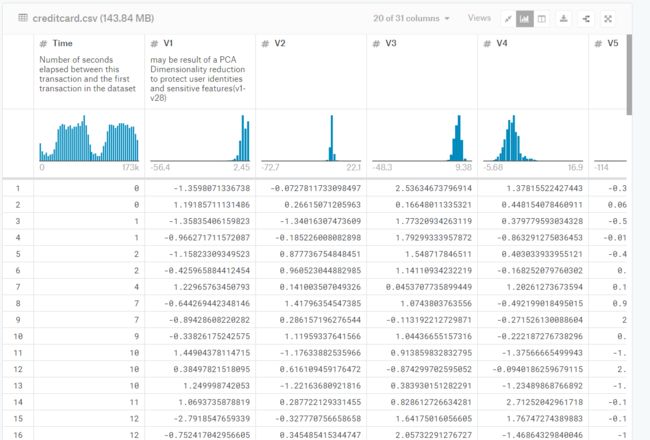
数据集来源于Kaggle平台,包含欧洲持卡人于2013年9月通过信用卡进行的交易,此数据集显示两天内发生的交易,其中284807笔交易中有492笔被盗刷。如果发生被盗刷,则取值1,否则为0
二、模型选择
原始数据集如下
通过观察数据集,我们可以分析出以下几点:
(1)每一笔刷卡交易都由28维特征加上时间和交易金额来表示,即30维向量
(2)V1到V28数值特征都经过PCA转化为结构化数据
(3)每一笔交易的标签均属于两类:正常交易为0,欺诈交易为1
数据场景本质是一个二分类问题,且每条数据都打好了标签,因此我们可以用监督式学习的二分类算法来建立场景模型
至此我们构建整个场景工程的步骤为:
(1)数据探索—EDA
(2)特征工程
(3)模型训练和评估
(4)模型调优
下面我们开始一步步构建整个场景工程
三、数据探索
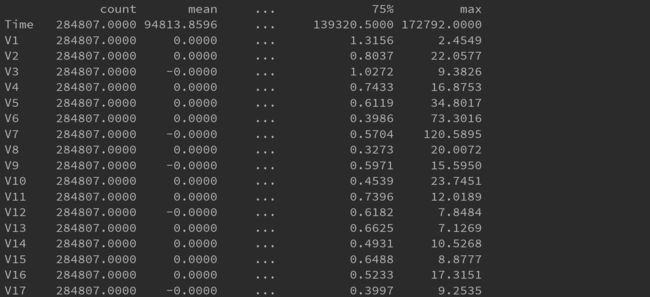
我们对数据初步查看和统计
通过查看数据信息得知,数据的类型基本是float64(PCA转换结果)
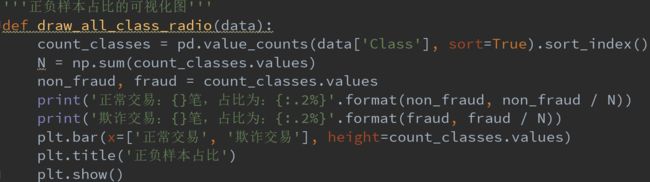
3.1、正负样本的占比
通过上图可知:可以看到正负样本极度失衡,且不在一个数量级上
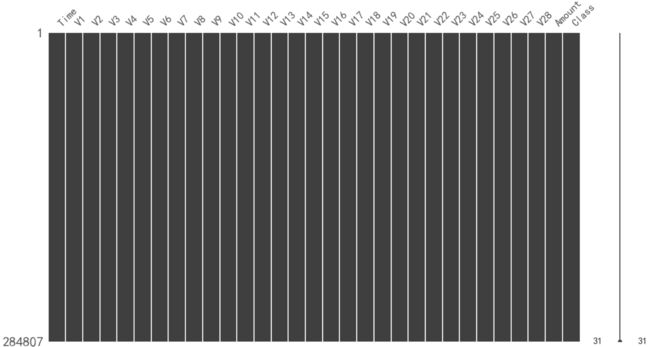
3.2、缺省值检测
通过上图可知:数据集不存在缺省值,因此不需作缺省值处理
3.3、单一特征在所有类别中的分布
我们可以观察某个特征(如Time或者Amount)在不同Class中的分布情况
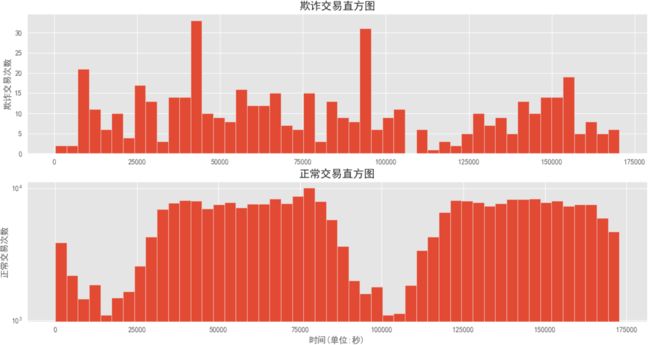
观察Time在不同Class中的分布情况:
通过上图可知:信用卡欺诈交易与时间不存在周期性,而正常的交易与时间存在类似双峰的周期性
从业务上也许说明:信用卡盗刷者为了不引起信用卡卡主的注意,更偏向选择信用卡卡住睡觉的时间或正常消费频率较高的时段来作案
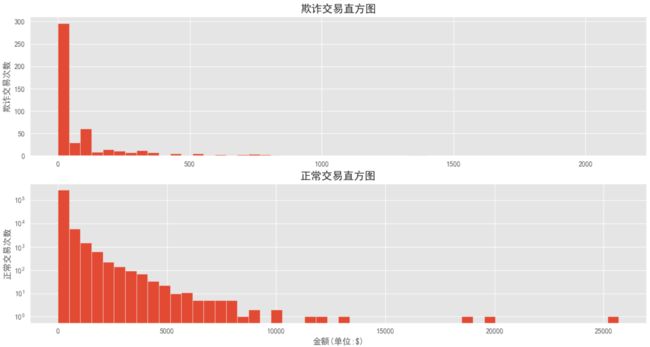
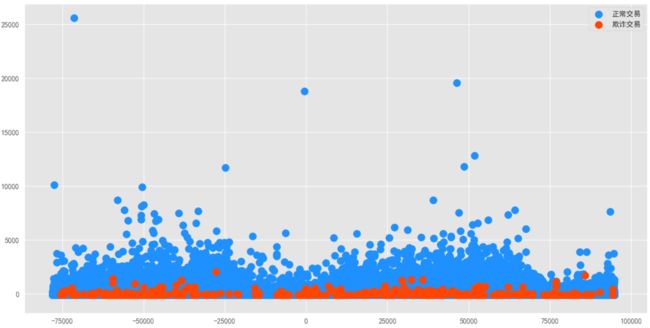
观察Amount在不同Class中的分布情况:
通过上图可知:信用卡欺诈交易的金额量比起正常交易要小的多
从业务上也许说明:信用卡盗刷者为了不引起信用卡卡主的注意,更偏向选择小金额消费来作案
3.4、每个特征在所有类别中的分布
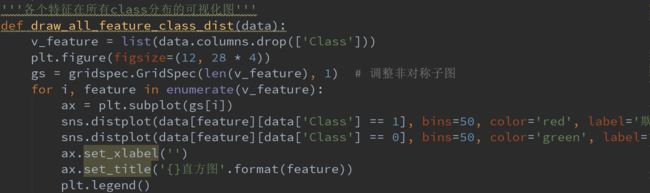
我们通过集成了分箱和核密度估计的displot来观察每个特征在所有类别中的分布
上图是不同特征分别在信用卡被盗刷和信用卡正常中的分布情况,其中:
(1)红色表示该特征在欺诈中的分布,绿色表示该特征在正常中的分布
(2)两个分布的交叉面积越大,则以该特征作为分类的区分度越小,如V15特征
(3)两个分布的交叉面积越小,则以该特征作为分类的区分度越大,如V14特征
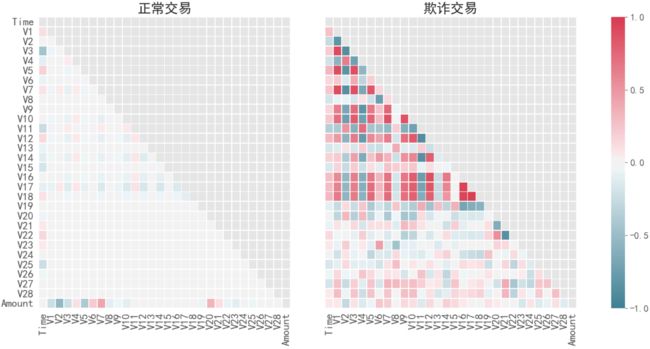
3.5、彼此特征之间的相关性矩阵
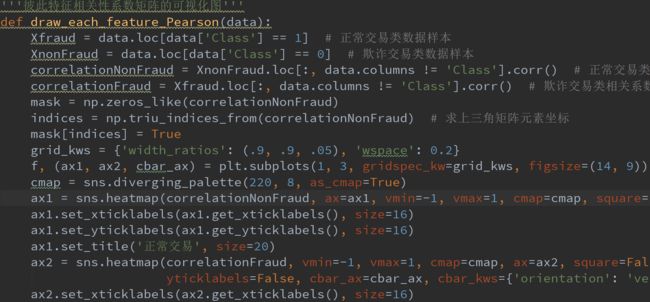
我们还可以分别观察彼此特征之间的相关性
通过上图可知:在欺诈交易中,一部分特征的相关性较为明显,如V12、V17、V18等
3.6、高维特征空间在低维空间的分布
我们也可将每个30维特征的样本降维到2维,即将高维度特征空间映射到低维度来观察其分布
通过上图可知:由于我们用PCA降维,欺诈点和正常点分布基本重合,分类分布丢失
因为PCA属于非监督学习且按照方差最大化来投影,其分类效果不好,为此在后续特征工程中,如果要对数据进行降维处理,我们会使用监督学习如LDA算法
四、特征工程
做完上述数据探索分析,接下来我们进入特征工程处理
4.1、特征标准化
由于特征Time和Amount的规格和其余特征差距较大,我们对它们进行标准化
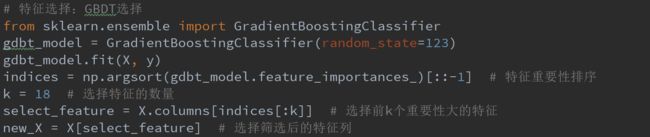
4.2、特征选择
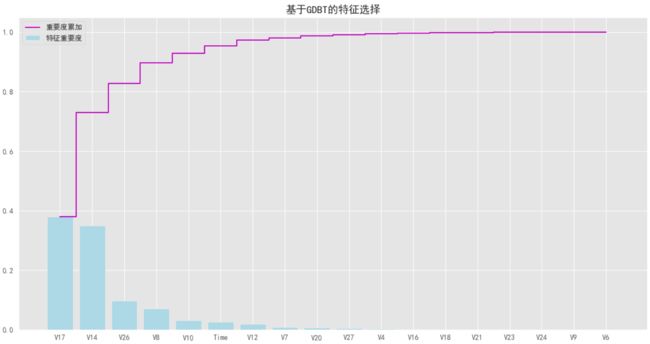
我们使用Embedded集成法的树模型—GBDT来完成特征选择
通过上图可知:我们通过GDBT将特征从31个缩减至18个
4.3、数据降维
由于数据均打上分类标签,我们对筛选后的特征样本使用LDA算法降维
五、模型训练和评估
做完上述特征工程后,接下来我们进入建模
5.1、处理训练集样本不平衡
在进行模型训练前,由于正负样本极度不平衡,会对模型学习造成困扰,因此我们需要解决样本不平衡问题
一般处理样本不平衡有上采样和下采样两种方法
(1)上采样:对样本中数量较少的那一类进行生成算法补齐,使之达到与较多的那一类样本相匹配的数量,如SMOTO算法
(2)下采样:从数量比较多的那类样本中,随机选出和与数量比较少的那类样本数量相同的样本,最终组成正负样本数量相同的样本集
这里我们选择上采样,对训练集使用SMOTO算法来平衡正负样本
PS:注意我们只对训练集进行过采样,测试集依然是真实数据
5.2、训练模型
接下来我们开始构建逻辑回归模型,用上采用平衡的训练集训练分类器
5.3、评估模型—混淆矩阵
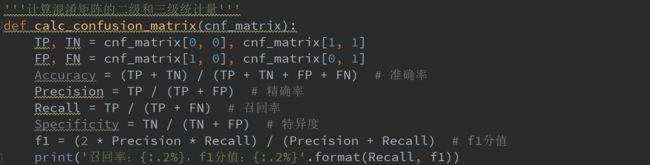
我们使用混淆矩阵来评估模型
这里需要知道几个一级统计量和二级统计量的统计定义
一级统计量:
(1)TP:真实值是positive,模型预测是positive的数量
(2)TN:真实值是negative,模型预测是negative的数量
(3)FP:真实值是negative,模型认为是positive的数量
(4)FN:真实值是positive,模型认为是negative的数量
二级统计量:
(1)准确率
准确率的统计意义是:在模型所有判断正确的结果中,占总观测值的占比
(2)精确率
精确率的统计意义是:在模型预测是positive的所有结果中,模型预测正确的占比
(3)召回率
召回率的统计意义是:在真实值是positive的所有结果中,模型预测正确的占比
(4)特异度
特异度的统计意义是:在真实值是negative的所有结果中,模型预测正确的占比
上面四个二级统计量一起呈现在表格中,就能得到如下这样一个矩阵,我们称它为混淆矩阵
我们用混淆矩阵在测试集上评估分类模型
其中F1分值是结合精确率Precision和召回率Recall的三级统计量
F1-Score的取值范围从0到1的,1代表模型的输出最好,0代表模型的输出结果最差
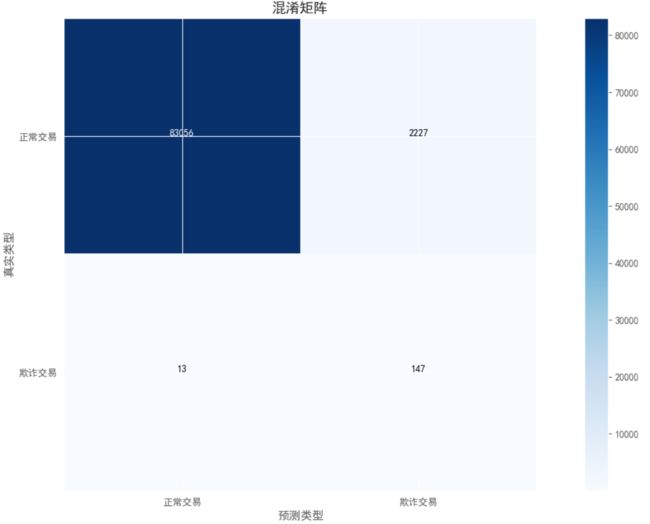
这个混淆矩阵的统计意义为:
(1)有13个欺诈交易,模型错误的预测成了正常交易(左下角)
(2)有2227个正常交易,模型错误的预测成了欺诈交易(右上角)
(3)有83056个正常交易,模型预测完全正确(上对角线)
(4)有147个欺诈交易,模型预测完全正确(下对角线)
六、模型调优
训练完模型,我们使用网格搜索在训练集上交叉验证对模型的超参数进行调优
场景模型里影响分类器的超参数的选择有以下几种情况:
(1)特征选择的数量和组合
(2)筛选后的特征数据是否降维
下面我们来观察在不同的操作情况和超参数下,模型在测试集上的评估结果
(1)18个特征 + 不降维处理
(2)14个特征 + 不降维处理
(3)18个特征 + 降维处理
(4)14个特征 + 降维处理
综合上述评估结果,我们可以看到:
(1)不同特征的组合影响模型的准确率
(2)如果特征数据不降维,则在测试集上,模型把正常交易判断错的概率大,而欺诈交易判断错的概率小
(3)如果特征数据降维,则在测试集上,模型把正常交易判断错的概率小,而欺诈交易判断错的概率大
七、总结
对于这个场景案例的整个建模工程,我们可以总结出:
(1)对于任意一份数据集,首先检查其数据类型和分布情况
(2)对于数据样例分布不平衡,应采取上采样或下采样使得数据样例达到平衡后,再进行模型的训练和调参
(3)模型的调参是一个痛苦的过程,不同的行为(如特征选择或降维算法)会产生不同的超参数组合,需要不断的试验来获取最佳参数
(4)模型的评估不该只依赖一个统计量(如准确率),而应该综合考虑召回率、F1值等混淆矩阵多个统计量
案例代码见:信用卡反欺诈消费预测模型