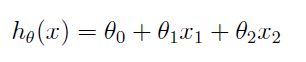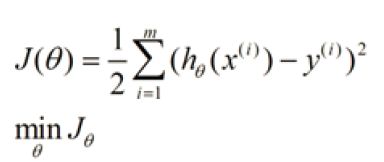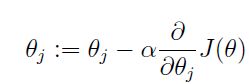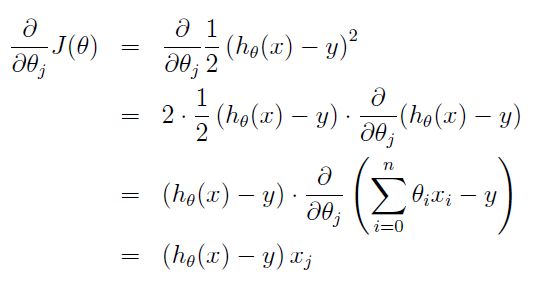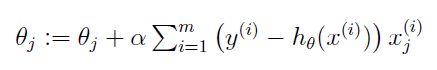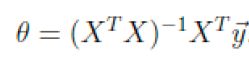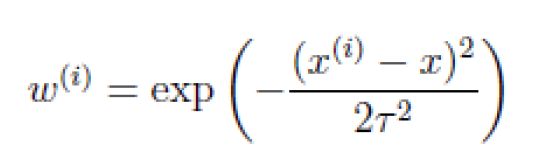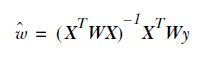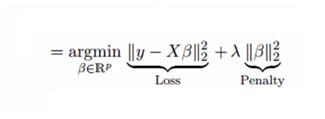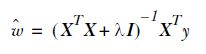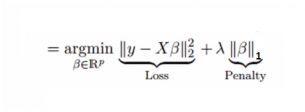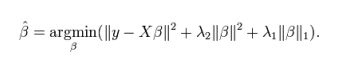线性回归
线性回归
** 令x0=1,方程转化为向量的方式: **
regression
** 损失函数或者错误函数： **
regression
** 求最小值，我们常用的方法有两种：梯度下降（又有批梯度下降BGD和随机梯度下降SGD） **
梯度下降
梯度下降
BGD
更新
SGD
** 批梯度下降的速度取决于α，另外批梯度下降每次的更新都要用到全部的训练数据，这会导致收敛的速度很慢，所以随机梯度下降只选择通过每个样本来更新迭代 **
SGD
最小二乘
*** 因为损失函数是一个凸函数，所以可以用最小二乘来求解最优解。求导，另导数为0，可得： ***
最小二乘
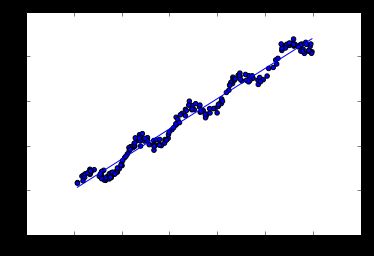
Python使用最小二乘求解线性方程（示例来自机器学习实战第8章）
%matplotlib inline
from numpy import *
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split('\t')) - 1
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = []
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
def standRegress(xArr,yArr):
xMat = mat(xArr)
yMat = mat(yArr).T
xTx = xMat.T*xMat
if linalg.det(xTx) == 0.0: #计算行列式 numpy.linalg.det
print "This matrix is singular,canot do inverse"
return
ws = xTx.I * (xMat.T*yMat)
return ws
xArr,yArr = loadDataSet('ex0.txt')
ws = standRegress(xArr,yArr)
import matplotlib.pyplot as plt
xMat = mat(xArr)
yMat = mat(yArr)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])
xCopy = xMat.copy()
xCopy.sort(0)
yHat = xCopy*ws
ax.plot(xCopy[:,1],yHat)
plt.show()
#相关系数
yHat = xMat*ws
corrcoef(yHat.T,yMat)
最小二乘
局部加权线性回归LWLR
** 基本假设： **
局部加权
wi
** 我们认为离x越近的样本权重越大，越远的权重越小。公式与高斯分布类似。 **
LWLR
def lwlr(testPoint,xArr,yArr,k = 1.0):
xMat = mat(xArr)
yMat = mat(yArr).T
m = shape(xMat)[0]
weights = mat(eye((m)))
for j in range(m):
diffMat = testPoint - xMat[j,:]
weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2))
xTx = xMat.T * (weights*xMat)
if linalg.det(xTx) == 0.0:
print "This matrix is singular,cannot do inverse"
return
ws = xTx.I * (xMat.T * (weights*yMat))
return testPoint * ws
def lwlrTest(testArr,xArr,yArr,k = 1.0):
m = shape(testArr)[0]
yHat = zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat
xArr,yArr = loadDataSet('ex0.txt')
yHat = lwlrTest(xArr,xArr,yArr,0.01)
import matplotlib.pyplot as plt
xMat = mat(xArr)
srtInd = xMat[:,1].argsort(0)
xSort = xMat[srtInd][:,0,:]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xSort[:,1],yHat[srtInd])
ax.scatter(xMat[:,1].flatten().A[0],mat(yArr).T.flatten().A[0],s = 2,c = 'red')
plt.show()
岭回归Ridge Regression
岭回归
Ridge
def ridgeRegres(xMat,yMat,lam = 0.2):
xTx = xMat.T * xMat
denom = xTx + eye(shape(xMat)[1])*lam
if linalg.det(denom) == 0.0:
print "This matrix is singular,cannot do inverse"
return
ws = denom.I * (xMat.T * yMat)
return ws
def ridgeTest(xArr,yArr):
xMat = mat(xArr)
yMat = mat(yArr).T
yMean = mean(yMat,0)
yMat = yMat - yMean
xMean = mean(xMat,0)
xVar = var(xMat,0)
xMat = (xMat - xMean)/xVar
numTestPts = 30
wMat = zeros((numTestPts,shape(xMat)[1]))
for i in range(numTestPts):
ws = ridgeRegres(xMat,yMat,exp(i - 10))
wMat[i,:] = ws.T
return wMat
xArr,yArr = loadDataSet('abalone.txt')
ridgeWeights = ridgeTest(xArr,yArr)
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(ridgeWeights)
plt.show()
Lasso回归
套索回归
前向逐步回归
def rssError(yArr,yHatArr):
return ((yArr - yHatArr)**2).sum()
def regularize(xMat):#regularize by columns
inMat = xMat.copy()
inMeans = mean(inMat,0) #calc mean then subtract it off
inVar = var(inMat,0) #calc variance of Xi then divide by it
inMat = (inMat - inMeans)/inVar
return inMat
def stageWise(xArr,yArr,eps=0.01,numIt = 100):
xMat = mat(xArr)
yMat = mat(yArr)
yMean = mean(yMat,0)
yMat = yMat - yMean
xMat = regularize(xMat)
m,n = shape(xMat)
returnMat = zeros((numIt,n))
ws = zeros((n,1))
wsTest = ws.copy()
wsMax = ws.copy()
for i in range(numIt):
print ws.T
lowestError = inf
for j in range(n):
for sign in [-1,1]:
wsTest = ws.copy()
wsTest[j] += eps*sign
yTest = xMat * wsTest
rssE = rssError(yMat.A,yTest.A)
if rssE < lowestError:
lowestError = rssE
wsMax = wsTest
ws = wsMax.copy()
returnMat[i,:] = ws.T
return returnMat
xArr,yArr = loadDataSet('abalone.txt')
stageWise(xArr,yArr,0.01,100)
ElasticNet回归
Lasso和Ridge回归技术的混合体。它会事先训练L1和L2作为惩罚项。这里尝试使用spark mllib：
Elastic Net
public class LinearRegressionExample {
/**
* 日志控制
*/
static{
LogSetting.setWarningLogLevel("org");
LogSetting.setWarningLogLevel("akka");
LogSetting.setWarningLogLevel("io");
LogSetting.setWarningLogLevel("httpclient.wire");
}
public static void main(String[] args) {
String resources = Thread.currentThread().getContextClassLoader().getResource("").getPath();
// PropertyConfigurator.configure(resources + "log4j.properties");
System.out.println(resources);
SparkConf conf = new SparkConf().setAppName("Logistic Regression with Elastic Net Example").setMaster("local[2]");
SparkContext sc = new SparkContext(conf);
SQLContext sql = new SQLContext(sc);
String path = resources + "libsvm_data.txt";
DataFrame training = sql.createDataFrame(MLUtils.loadLibSVMFile(sc, path).toJavaRDD(), LabeledPoint.class);
LinearRegression lr = new LinearRegression().setMaxIter(10).setRegParam(0.3).setElasticNetParam(0.8);
LinearRegressionModel lrModel = lr.fit(training);
System.out.println("Weights: " + lrModel.weights() + " Intercept: " + lrModel.intercept());
LinearRegressionTrainingSummary trainingSummary = lrModel.summary();
System.out.println("numIterations: " + trainingSummary.totalIterations());
System.out.println("objectiveHistory: " + Vectors.dense(trainingSummary.objectiveHistory()));
trainingSummary.residuals().show();
System.out.println("RMSE: " + trainingSummary.rootMeanSquaredError());
System.out.println("r2: " + trainingSummary.r2());
}
}