排序算法：Python 实现

import sys
print (sys.version)   # 3.5.2 |Continuum Analytics, Inc.| (default, Jul  5 2016, 11:41:13) [MSC v.1900 64 bit (AMD64)]

---

1. 交换排序 — 冒泡排序（Bubble Sort）

通过两两交换，小的先冒出来，大的后冒出来。O(N²)，稳定，排序过程如下：

代码如下：

def bubble_sort(num):
    n = len(num)
    for i in range(n):
        for j in range(i, n):
            if num[i] > num[j]:
                num[i], num[j] = num[j], num[i]
    return num

算法的稳定性定义为：对于待排序列中相同元素的原来次序不被排序算法改变，则称该算法稳定。

2. 交换排序 — 快速排序（Quick Sort）

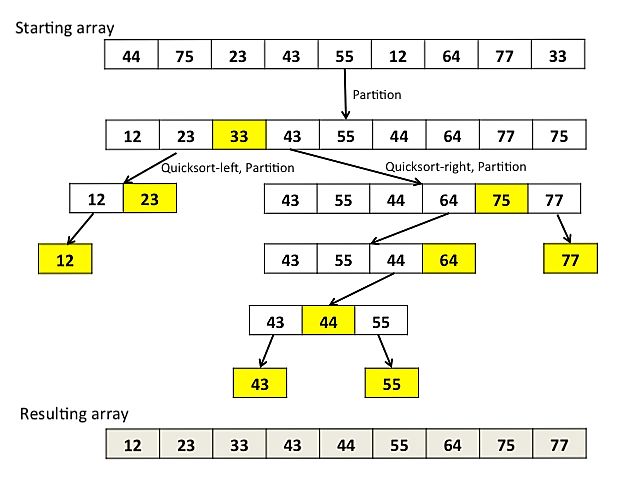
1). 首先选择一个基准元素，通常选择第一个元素或者最后一个元素。
2). 通过一轮排序，将待排序的数组分割成独立的两部分，其中一部分数组的元素值均比基准元素值小，另一部分数组的元素值比基准值大。
3). 然后分别对这两部分数组用同样的方法继续进行排序，直到整个数组有序。

O(NlogN)，不稳定，排序过程如下：

代码如下：

def quick_sort(num):
    if len(num) <= 1:
        return num
    larger = []
    smaller = []
    p = num.pop(random.randint(0, len(num)-1))   # 这里我们随机选择基准元素
    for i in num:
        if i <= p:
            smaller.append(i)
        else:
            larger.append(i)

    return quick_sort(smaller) + [p] + quick_sort(larger)

---

3. 选择排序 — 直接选择排序（Straight Selection Sort）

在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推。O(N²)，不稳定。

代码如下：

def selection_sort(num):
    n = len(num)
    for i in range(n):
        min = i
        for j in range(i, n):
            if num[min] > num[j]:
                min = j
        num[min], num[i] = num[i], num[min]

    return num

---

4. 选择排序 — 堆排序（Heap Sort）

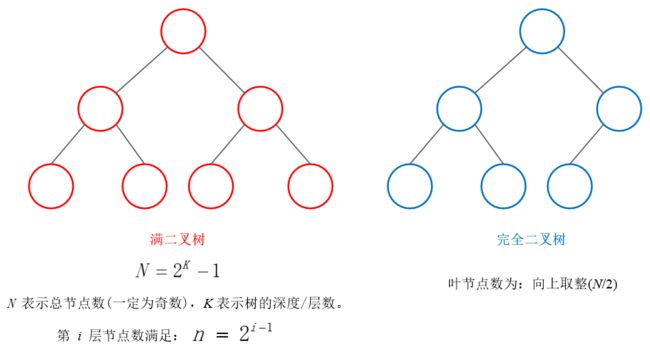
完全二叉树：叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点。

堆 是一种完全二叉树，堆排序是一种树形选择排序，利用了大顶堆堆顶元素最大的特点，不断取出最大元素，并调整使剩下的元素使之还是大顶堆，依次取出最大元素就实现了排序。O(NlogN)，不稳定。 举例如下：

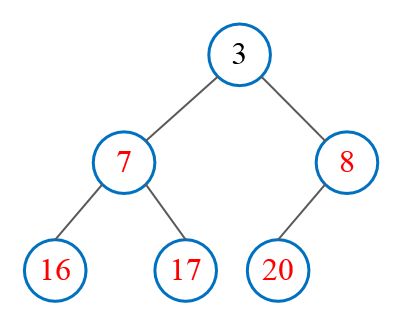
待排序列： [16, 7, 3, 20, 17, 8]
首先根据该序列构建一个完全二叉树，得到：

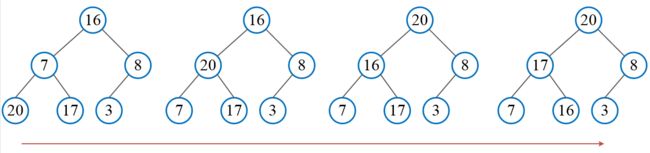
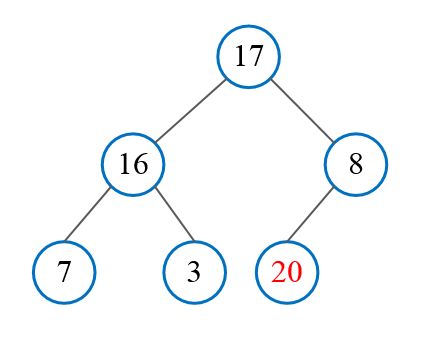
然后需要构造初始堆，从最后一个非叶节点开始调整（从右往左，从下至上），调整过程如下，得到 初始堆：

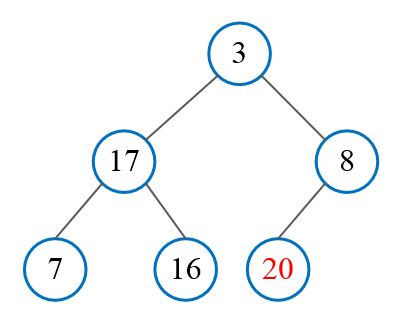
得到初始堆后，将堆顶元素与最后一个元素交换，得到：

此时3位于堆顶，不满足大顶堆的性质，需调整如下（忽略最后一个元素）：

然后继续将堆顶元素与倒数第二个元素交换，如此进行下去，最终得到：

代码如下：

def MAX_Heapify(heap,HeapSize,root):   #在堆中做调整使得父节点的值大于子节点
    left = 2*root + 1   # 左子节点
    right = left + 1    # 右子节点
    larger = root
    if left < HeapSize and heap[larger] < heap[left]:
        larger = left
    if right < HeapSize and heap[larger] < heap[right]:
        larger = right
    if larger != root:  #如果做了堆调整则larger的值等于左节点或者右节点，则对调值
        heap[larger], heap[root] = heap[root], heap[larger]
        MAX_Heapify(heap, HeapSize, larger)


def Build_MAX_Heap(heap):   # 构造一个堆，然后调整成最大堆
    HeapSize = len(heap)
    for i in range((HeapSize-2)//2,-1,-1):   # 从最后一个非叶节点往前开始调整
        MAX_Heapify(heap,HeapSize,i)


def HeapSort(heap):
    Build_MAX_Heap(heap)   # 得到初始(大顶)堆
    #print(heap)
    for i in range(len(heap)-1,-1,-1):
        heap[0], heap[i] = heap[i], heap[0]    # 堆顶元素与最后一个元素交换
        MAX_Heapify(heap, i, 0)
    return heap


if __name__ == '__main__':
    a = [16, 7, 3, 20, 17, 8]
    print (a)
    print (HeapSort(a))

---

5. 插入排序 — 直接插入排序（Straight Insertion Sort）

每次将一个待排序的元素与已排序好的元素进行逐一比较，直到找到合适的位置按大小插入。O(N²)，稳定。排序过程如下：

代码如下：

def insertion_sort(num):
    for i in range(1,len(num)):
        j = i
        tmp = num[i]
        while j > 0 and tmp < num[j-1]:
            num[j] = num[j-1]
            j -= 1
        num[j] = tmp

    return num

print (insertion_sort(num))

---

6. 插入排序 — 希尔排序（Shell Sort）

先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。O(N^1.3)，不稳定。

排序过程如下（下面希尔排序的步长选择都是从n/2开始，每次再减半，直到最后为1）：

代码如下：

def shell_sort(lists):
    count = len(lists)
    step = 2
    group = count // step
    while group > 0:
        for i in range(0, group):
            j = i + group
            while j < count:
                k = j - group
                key = lists[j]
                while k >= 0:
                    if lists[k] > key:
                        lists[k+group] = lists[k]
                        lists[k] = key
                    k -= group
                j += group
        group //= step
    return lists

print(shell_sort([49,38,65,97,26,13,27,49,55,4]))

---

7. 归并排序（Merge Sort）

归并排序是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。简单来讲，就是将待排序列不停的分为左边和右边两份，然后以此递归分下去。然后再将她们按照两个有序数组的样子合并起来。O(NlogN)，稳定。

举例如下（引自博文）：

代码如下：

def merge(left,right):
    i, j = 0, 0
    result = []
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1

    result += left[i:]
    result += right[j:]
    return result


def MergeSort(list):
    if len(list) <= 1:
        return list
    mid = len(list)//2
    left = MergeSort(list[:mid])
    right = MergeSort(list[mid:])
    return merge(left, right)


if __name__ == '__main__':
    a = [16, 7, 3, 20, 17, 8]
    print (a)
    print (MergeSort(a))