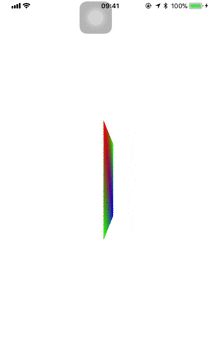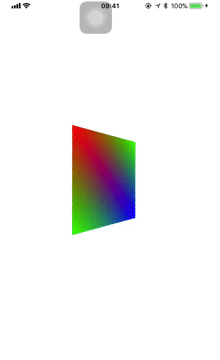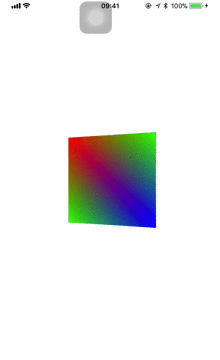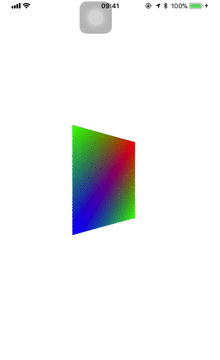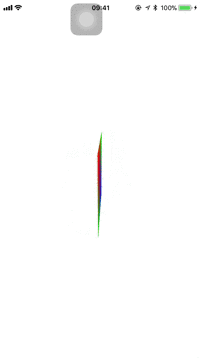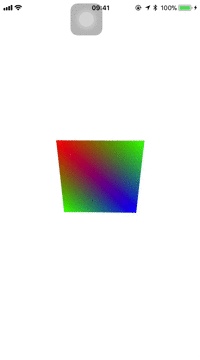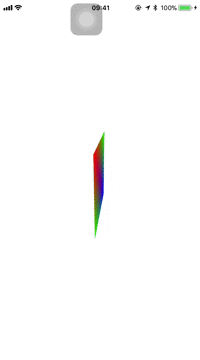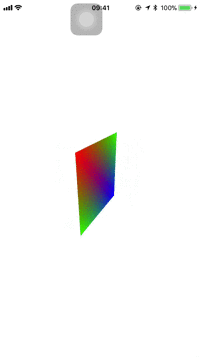iOS开发学习OpenGL ES系列 -- 摄像机

在讲摄像机之前先介绍一下3D渲染中的MVP：分别是模型矩阵（model）、观察矩阵（view）、投影矩阵（Projection）。其中模型矩阵操作的是单个3D模型，可以进行平移、缩放、旋转或者组合变换。观察矩阵可以理解为3D世界中的摄像机，当摄像机的位置发生改变，拍摄的角度不一样，呈现在屏幕上的效果自然会有变化。这一操作会改变物体的顶点位置。投影矩阵在上一篇讲过，分为正射投影和透视投影，透视投影有远小近大的效果，更为真实。这里大概了解一下MVP，接下来修改代码正式步入3D世界，这里引入了三个矩阵，所以顶点着色器中需要添加接受属性：

attribute vec4 position;
attribute vec4 color;

varying vec4 fColor;

uniform mat4 pMatrix;
uniform mat4 vMatrix;
uniform mat4 mMatrix;

void main(void) {
    fColor = color;
    mat4 mvp = pMatrix * vMatrix * mMatrix;
    gl_Position = mvp * position;
}

mMatrix、vMatrix、pMatrix分别是模型矩阵、观察矩阵、投影矩阵。这里将mvp直接相乘，结果再与position相乘。注意相乘的顺序先进行模型矩阵变换，再是观察矩阵，最后是投影矩阵变换。

相应的工程中添加三个属性：

GLKMatrix4 projectionMatrix; // 投影矩阵
GLKMatrix4 modelMatrix; // 模型矩阵
GLKMatrix4 cameraMatrix; // 观察矩阵

在viewDidLoad中进行初始化：

// projectionMatrix 投影矩阵。 呈现更为真实的3D效果这里设置投影矩阵为透视投影。
 float aspect = self.view.frame.size.width / self.view.frame.size.height;
 float fovyRadians =GLKMathDegreesToRadians(90);
 projectionMatrix = GLKMatrix4MakePerspective(fovyRadians, aspect, 0.0, 100.0);
 
 // modelMatrix 模型矩阵 初始化模型矩阵为单位矩阵
 modelMatrix = GLKMatrix4Identity;
 
 // cameraMatrix 观察矩阵
 cameraMatrix = GLKMatrix4MakeLookAt(0, 0, 2, 0, 0, 0, 0, 1, 0);

GLKit提供了创建观察矩阵的函数：
GLKMatrix4MakeLookAt(float eyeX, float eyeY, float eyeZ, float centerX, float centerY, float centerZ, float upX, float upY, float upZ)

参数float eyeX, float eyeY, float eyeZ定义摄像机的位置。float centerX, float centerY, float centerZ摄像机看向的点。光是这样还不行，相机还可以自转360.所以还需要float upX, float upY, float upZ三个参数确定相机向上的朝向。我们可以设置这9个参数以控制摄像机从不同的角度观察物体。

目前创建的观察矩阵是固定的不动的，我们把projectionMatrix、modelMatrix和cameraMatrix赋值到Vertex Shader:

GLuint modeLocation = glGetUniformLocation(program, "mMatrix");
glUniformMatrix4fv(modeLocation, 1, 0, modelMatrix.m);
    
GLuint projectionLocation = glGetUniformLocation(program, "pMatrix");
glUniformMatrix4fv(projectionLocation, 1, 0, projectionMatrix.m);
    
GLuint cameraLocation = glGetUniformLocation(program, "vMatrix");
glUniformMatrix4fv(cameraLocation, 1, 0, cameraMatrix.m);

运行效果:

这跟前面的透视投影没什么区别。上一篇中视点在（0，0，0）位置，可视区域在Z轴负方向，成像在（0，0，0）和可视区域之间。而这里设置相机在（0，0，2）位置，朝向（0，0，0）也就是Z的负方向，其余设置一样。所以这里创建观察矩阵其实就是代替了上一篇中的视点，所以展示效果是一样的。只不过前面的默认视点在（0，0，0）位置固定不动，而这里我们可以通过修改GLKMatrix4MakeLookAt的参数来控制相机位置与方向，以展示出物体不同角度的图像。下面我们重新定义观察矩阵：

// cameraMatrix = GLKMatrix4MakeLookAt(0, 0, 2, 0, 0, 0, 0, 1, 0);
cameraMatrix = GLKMatrix4MakeLookAt(0, 1, 2, 0, 0, 0, 0, 1, 0);

把相机的y轴改为1，看一下效果：

改变了相机的y值，朝向和向上不变，很明显有俯视向下看的感觉。

// cameraMatrix = GLKMatrix4MakeLookAt(0, 1, 2, 0, 0, 0, 0, 1, 0);
cameraMatrix = GLKMatrix4MakeLookAt(0, sin(change), 3, 0, 0, 0, 0, 1, 0);

这次让相机的y在[-1,1]之间变化，修改z为3，并去掉旋转，看下效果：

首先看到的图像肯定是变小了，这是因为相机的z修改为3，把距离拉远了1个单位。再观察感觉矩形是在绕着X轴自转，其实并不这样，因为我们改变相机的y是在[-1,1]之间，并且z是固定的，所以只能是直线性的上下移动，也就造成了这种最终效果。

这里还可以修改GLKMatrix4MakeLookAt的float upX, float upY, float upZ来控制相机的向上朝向。

// cameraMatrix = GLKMatrix4MakeLookAt(0, sin(change), 3, 0, 0, 0, 0, 1, 0);
cameraMatrix = GLKMatrix4MakeLookAt(0, sin(change), 3, 0, 0, 0, 1, 0, 0);

这里设置相机朝向为x正方向，效果图就不上传了，有兴趣的可以自己尝试修改这些参数来控制相机。当然需要注意的是物体的可视区域与相机位置。否则你有可能什么都看不到。

关于OpenGL ES的相机就说到这里了，如果文中有错误或者有补充的知识点欢迎留言讨论，谢谢！

本例源码：LearningOpenGL ES GitHub

如果修改相机的向上朝向为X正方向的话，屏幕上的 图像会逆时针旋转90度，而且再不是上下摆动，变成了左右摆动。这是因为相机向上朝向由Y的正方向变为X的正方向，相机旋转了90度，原来的右上角为绿色，旋转之后变为蓝色。原来是Y轴朝上，相机是上下滑动变为现在的X轴朝上而左右滑动。