前言
排序算法可能是你学编程第一个学习的算法,还记得冒泡吗?
当然,排序和查找两类算法是面试的热门选项。如果你是一个会写快排的程序猿,面试官在比较你和一个连快排都不会写的人的时候,会优先选择你的。那么,前端需要会排序吗?答案是毋庸置疑的,必须会。现在的前端对计算机基础要求越来越高了,如果连排序这些算法都不会,那么发展前景就有限了。本篇将会总结一下,在前端的一些排序算法。
正文
Array.sort
相信每个使用js的都用过这个函数,但是,这个函数本身有些优点和缺点。我们可以通过一个例子来看一下它的功能:
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 100, 50];
console.log(arr.sort()); // [ 1, 10, 100, 11, 12, 20, 22, 24, 30, 31, 50, 55, 88 ]
console.log(arr.sort((item1, item2) => item1 - item2)); // [ 1, 10, 11, 12, 20, 22, 24, 30, 31, 50, 55, 88, 100 ]
相信你也已经看出来它在处理上的一些差异了吧。首先,js中的sort会将排序的元素类型转化成字符串进行排序。不过它是一个高阶函数,可以接受一个函数作为参数。而我们可以通过传入内部的函数,来调整数组的升序或者降序。
sort函数的性能:相信对于排序算法性能来说,时间复杂度是至关重要的一个参考因素。那么,sort函数的算法性能如何呢?通过v8引擎的源码可以看出,Array.sort是通过javascript来实现的,而使用的算法是快速排序,但是从源码的角度来看,在实现上明显比我们所使用的快速排序复杂多了,主要是做了性能上的优化。所以,我们可以放心的使用sort()进行排序。
冒泡排序
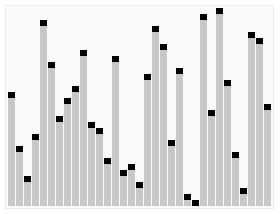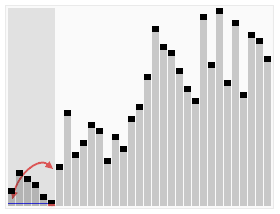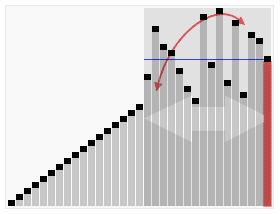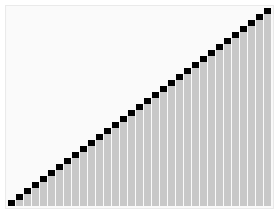
冒泡排序,它的名字由来于一副图——鱼吐泡泡,泡泡越往上越大。
思路:第一次循环,开始比较当前元素与下一个元素的大小,如果比下一个元素小或者相等,则不需要交换两个元素的值;若比下一个元素大的话,则交换两个元素的值。然后,遍历整个数组,第一次遍历完之后,相同操作遍历第二遍。
图例:
代码实现:
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 100, 50];
function bubbleSort(arr){
for(let i = 0; i < arr.length - 1; i++){
for(let j = 0; j < arr.length - i - 1; j++){
if(arr[j] > arr[j + 1]){
swap(arr, j, j+1);
}
}
}
return arr;
}
function swap(arr, i, j){
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
console.log(arr);
性能:
时间复杂度:平均时间复杂度是O(n^2)
空间复杂度:由于辅助空间为常数,所以空间复杂度是O(1);
改进:
我们可以对冒泡排序进行改进,使得它的时间复杂度在大多数顺序的情况下,减小到O(n);
1.加一个标志位,如果没有进行交换,将标志位置为false,表示排序完成。
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 100, 50];
function swap(arr, i, j){
const temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
for(let i = 0; i < arr.length - 1; i++){
let flag = false;
for(let j = 0; j < arr.length - 1 - i; j++){
if(arr[j] > arr[j+1]){
swap(arr, j, j+1);
flag = true;
}
}
if(!flag){
break;
}
}
console.log(arr); //[ 1, 10, 11, 12, 20, 22, 24, 30, 31, 50, 55, 88, 100 ]
2.记录最后一次交换的位置, 因为最后一次交换的数,是在这一次排序当中最大的数,之后的数都比它大。在最佳状态时,时间复杂度也会缩小到O(n);
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 100, 50 ,112];
function swap(arr, i, j){
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp
}
function improveBubble(arr, len){
for(let i = len - 1; i >= 0; i--){
let pos = 0;
for(let j = 0; j < i; j++){
if(arr[j] > arr[j+1]){
swap(arr, j, j+1);
pos = j + 1;
}
}
len = pos + 1;
}
return arr;
}
console.log(improveBubble(arr, arr.length)); // [ 1, 10, 11, 12, 20, 22, 24, 30, 31, 50, 55, 88, 100, 112 ]
选择排序
选择排序,即每次都选择最小的,然后换位置
思路:
第一遍,从数组中选出最小的,与第一个元素进行交换;第二遍,从第二个元素开始,找出最小的,与第二个元素进行交换;依次循环,完成排序
图例:
代码实现:
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 31, 88, 12, 100, 50];
function swap(arr, i, j){
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
function selectionSort(arr){
for(let i = 0; i < arr.length - 1; i++){
let index = i;
for(let j = i+1; j < arr.length; j++){
if(arr[index] > arr[j]){
index = j;
}
}
swap(arr, i, index);
}
return arr;
}
console.log(selectionSort(arr)); // [ 1, 10, 11, 12, 20, 22, 24, 30, 31, 50, 55, 88, 100 ]
性能:
时间复杂度:平均时间复杂度是O(n^2),这是一个不稳定的算法,因为每次交换之后,它都改变了后续数组的顺序。
空间复杂度:辅助空间是常数,空间复杂度为O(1);
插入排序
插入排序,即将元素插入到已排序好的数组中
图例:
代码实现:
const arr = [1, 20, 10, 30, 22, 11, 55, 24, 0, 31, 88, 12, 100, 50 ,112];
function insertSort(arr){
for(let i = 0; i < arr.length; i++){
let temp = arr[i];
for(let j = 0; j < i; j++){
if(temp < arr[j] && j === 0){
arr.splice(i, 1);
arr.unshift(temp);
break;
}else if(temp > arr[j] && temp < arr[j+1] && j < i - 1){
arr.splice(i, 1);
arr.splice(j+1, 0, temp);
break;
}
}
}
return arr;
}
console.log(insertSort(arr)); // [ 0, 1, 10, 11, 12, 20, 22, 24, 30, 31, 50, 55, 88, 100, 112 ]
性能:
时间复杂度:平均算法复杂度为O(n^2)
空间复杂度:辅助空间为常数,空间复杂度是O(1)
我们仨之间
其实,三个算法都是难兄难弟,因为算法的时间复杂度都是在O(n^2)。在最坏情况下,它们都需要对整个数组进行重新调整。只是选择排序比较不稳定。
快速排序
快速排序,从它的名字就应该知道它很快,时间复杂度很低,性能很好。它将排序算法的时间复杂度降低到O(nlogn)
思路:
首先,我们需要找到一个基数,然后将比基数小的值放在基数的左边,将比基数大的值放在基数的右边,之后进行递归那两组已经归类好的数组。
图例:
原图片太大,放一张小图,并且附上原图片地址,有兴趣的可以看一下:
代码实现:
const arr = [30, 32, 6, 24, 37, 32, 45, 21, 38, 23, 47];
function quickSort(arr){
if(arr.length <= 1){
return arr;
}
let temp = arr[0];
const left = [];
const right = [];
for(var i = 1; i < arr.length; i++){
if(arr[i] > temp){
right.push(arr[i]);
}else{
left.push(arr[i]);
}
}
return quickSort(left).concat([temp], quickSort(right));
}
console.log(quickSort(arr));
性能:
时间复杂度:平均时间复杂度O(nlogn),只有在特殊情况下会是O(n^2),不过这种情况非常少
空间复杂度:辅助空间是logn,所以空间复杂度为O(logn)
归并排序
归并排序,即将数组分成不同部分,然后注意排序之后,进行合并
思路:
首先,将相邻的两个数进行排序,形成n/2对,然后在每两对进行合并,不断重复,直至排序完。
图例:
代码实现:
//迭代版本
const arr = [3,44,38,5,47,15,36,26,27,2,46,4,19,50,48]
function mergeSort(arr){
const len = arr.length;
for(let seg = 1; seg < len; seg += seg){
let arrB = [];
for(let start = 0; start < len; start += 2*seg){
let row = start, mid = Math.min(start+seg, len), heig = Math.min(start + 2*seg, len);
let start1 = start, end1 = mid;
let start2 = mid, end2 = heig;
while(start1 < end1 && start2 < end2){
arr[start1] < arr[start2] ? arrB.push(arr[start1++]) : arrB.push(arr[start2++]);
}
while(start1 < end1){
arrB.push(arr[start1++]);
}
while(start2 < end2){
arrB.push(arr[start2++]);
}
}
arr = arrB;
}
return arr;
}
console.log(mergeSort(arr));
//递归版
const arr = [3,44,38,5,47,15,36,26,27,2,46,4,19,50,48];
function mergeSort(arr, seg = 1){
const len = arr.length;
if(seg > len){
return arr;
}
const arrB = [];
for(var start = 0; start < len; start += 2*seg){
let low = start, mid = Math.min(start+seg, len), heig = Math.min(start+2*seg, len);
let start1 = low, end1 = mid;
let start2 = mid, end2 = heig;
while(start1 < end1 && start2 < end2){
arr[start1] < arr[start2] ? arrB.push(arr[start1++]) : arrB.push(arr[start2++]);
}
while(start1 < end1){
arrB.push(arr[start1++]);
}
while(start2 < end2){
arrB.push(arr[start2++]);
}
}
return mergeSort(arrB, seg * 2);
}
console.log(mergeSort(arr));
性能:
时间复杂度:平均时间复杂度是O(nlogn)
空间复杂度:辅助空间为n,空间复杂度为O(n)
基数排序
基数排序,就是将数的每一位进行一次排序,最终返回一个正常顺序的数组。
思路:
首先,比较个位的数字大小,将数组的顺序变成按个位依次递增的,之后再比较十位,再比较百位的,直至最后一位。
图例:
代码实现:
const arr = [3221, 1, 10, 9680, 577, 9420, 7, 5622, 4793, 2030, 3138, 82, 2599, 743, 4127, 10000];
function radixSort(arr){
let maxNum = Math.max(...arr);
let dis = 0;
const len = arr.length;
const count = new Array(10);
const tmp = new Array(len);
while(maxNum >=1){
maxNum /= 10;
dis++;
}
for(let i = 1, radix = 1; i <= dis; i++){
for(let j = 0; j < 10; j++){
count[j] = 0;
}
for(let j = 0; j < len; j++){
let k = parseInt(arr[j] / radix) % 10;
count[k]++;
}
for(let j = 1; j < 10; j++){
count[j] += count[j - 1];
}
for(let j = len - 1; j >= 0 ; j--){
let k = parseInt(arr[j] / radix) % 10;
tmp[count[k] - 1] = arr[j];
count[k]--;
}
for(let j = 0; j < len; j++){
arr[j] = tmp[j];
}
radix *= 10;
}
return arr;
}
console.log(radixSort(arr));
性能:
时间复杂度:平均时间复杂度O(k*n),最坏的情况是O(n^2)
总结
我们一共实现了6种排序算法,对于前端开发来说,熟悉前面4种是必须的。特别是快排,基本面试必考题。本篇的内容总结分为六部分:
冒泡排序
选择排序
插入排序
快速排序
归并排序
基数排序
排序算法,是算法的基础部分,需要明白它的原理,总结下来排序可以分为比较排序和统计排序两种方式,本篇前5种均为比较排序,基数排序属于统计排序的一种。希望看完的你,能够去动手敲敲代码,理解一下
引文地址:https://segmentfault.com/a/1190000011294349