介绍哈夫曼编码之前先介绍一下哈弗曼树:
哈夫曼树:哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度 为叶结点的层数)。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+...+Wn*Ln) ,N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。
哈夫曼树的构造:
一、构成初始集合
对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,...,Ti,...,Tn},其中每棵二叉树Ti中只有一个权值为Wi的根结点,它的左右子树均为空。(为方便在计算机上实现算法,一般还要求以Ti的权值Wi的升序排列。)
二、选取左右子树
在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树,新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、删除左右子树
从F中删除这两棵树,并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步,
重复二和三两步,直到集合F中只有一棵二叉树为止。
构造过程如下:
(a) 有权值为1,2,3,4四棵树;
(b) 由于树1,2的权值处于最小和次最小,所以选中,并合成为一棵树,小的权值位于左边;
(c) 从3,4,(1,2 = 3)三棵树里面选择权值最小的和次小的,我们选中3和(1,2)
合成新树(3,(1,2)= 6);
(d) 最后选出新树(4,(3,(1, 2)))
哈夫曼树具体实现
需要考虑的问题:
(1) 用什么样的存储结构;
(2) 怎么选择选择最小和次小权值的树;
(3) 怎么存放合成的新树
如果我们采用
Struct node
{
Int key;
Struct node *l;
Struct node *r;
}
的存储结构的话,可以采用数组的链式结构,并设计标记数组如下:
(我们以4个初始树为例子)
标记数组:(有则标记为1,否则为0)
| Struct node n1 |
Struct node n1 |
Struct node n1 |
Struct node n1 |
存储数组
| Struct node n1 |
Struct node n1 |
Struct node n1 |
Struct node n1 |
第一次选择为1,2树,合成新树,我们可以统一放在最小树的位置上(也可以放在大树位置上),所以新树放于树1 的位置并更新其权值为两者之和,其状态为:
标记数组:(有则标记为1,否则为0)
| 1 |
0 |
1 |
1 |
存储数组
| Struct node n1 |
Free() |
Struct node n1 |
Struct node n1 |
这样存储结构的问题解决了,其实做到这里我们应该比较清楚后面怎么做了,当然选择出最小值和次小值为比较简单的算法了。
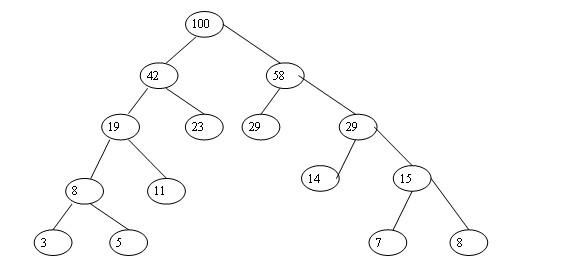
例:设有8个字符{A,B,C,D,E,F,G,H},其概率为{0.05,0.29,0.07,0.08,0.14,0.23,0.03,0.11},设其权值用整数表示为 {5,29,7,8,14,23,3,11},其哈夫曼树如图1所示。
实现代码如下:
1 #include2 #include 3 #include <string.h> 4 struct node 5 { 6 int key; 7 struct node *l; 8 struct node *r; 9 }; 10 typedef struct node *pnode; 11 int mark[100]; 12 struct node huffman[100]; 13 void PrintNode(const pnode node) 14 { 15 printf("key = %d \n", node->key); 16 } 17 void PreOrder(pnode T) 18 { 19 if(T) 20 21 { 22 PrintNode(T); 23 PreOrder(T->l); 24 25 PreOrder(T->r); 26 27 } 28 29 } 30 void Select(int *mark, struct node *huffman, int size, int *choose) 31 { 32 33 int i; 34 35 for(i = 0; i< size; i++) 36 { 37 if(mark[i]) 38 { 39 choose[0] = i; 40 i++; 41 break; 42 } 43 } 44 choose[1] = choose[0]; 45 for(; i < size; i++) 46 { 47 if(mark[i]) 48 { 49 if(huffman[choose[0]].key >= huffman[i].key) 50 { 51 choose[1] = choose[0]; 52 choose[0] = i; 53 54 55 } 56 else if(huffman[choose[1]].key > huffman[i].key) choose[1] = i; 57 58 59 } 60 61 } 62 } 63 void Choose(int *mark, struct node *huffman, int size, int *choose) 64 { 65 int i; 66 int minkey = 0; 67 int tkey = 0; 68 int temp = 0; 69 for(i = 0; i< size; i++) 70 { 71 if(mark[i]) 72 { 73 minkey = i; 74 i++; 75 break; 76 } 77 } 78 tkey = minkey; 79 for(; i< size; i++) 80 { 81 if(mark[i]) 82 { 83 if(huffman[i].key < huffman[minkey].key) 84 { 85 tkey = minkey; 86 minkey = i; 87 } 88 if(tkey == minkey) 89 tkey = i; 90 if(huffman[tkey].key > huffman[i].key && i != minkey) 91 { 92 tkey = i; 93 } 94 } 95 } 96 choose[0] = minkey; 97 choose[1] = tkey; 98 } 99 pnode HuffmanTree(int *mark, struct node *huffman, int size) 100 { 101 int choose[2]; 102 int i; 103 pnode mynode; 104 105 for(i = 0; i < size-1; i++) 106 { 107 Select(mark, huffman, size, choose); 108 mynode = (pnode)malloc(sizeof(struct node)); 109 mynode->key = huffman[choose[0]].key+huffman[choose[1]].key;//更新key值 110 mynode->l = (pnode)malloc(sizeof(struct node)); 111 mynode->l->key = huffman[choose[0]].key; 112 mynode->l->l = huffman[choose[0]].l; 113 mynode->l->r = huffman[choose[0]].r; 114 mynode->r = &huffman[choose[1]]; 115 huffman[choose[0]] = *mynode; 116 mark[choose[1]] = 0; 117 free(mynode); 118 } 119 return &huffman[choose[0]]; 120 } 121 int main(void) 122 { 123 int key[8] = {5,29,7,8,14,23,3,11}; 124 int i; 125 pnode huffmantree; 126 memset(mark, -1, sizeof(mark)); 127 memset(huffman, 0, sizeof(huffman)); 128 for(i = 0; i < 8; i++) 129 { 130 huffman[i].key = key[i]; 131 } 132 huffmantree = HuffmanTree(mark, huffman, 8); 133 PreOrder(huffmantree); 134 return 0; 135 }
哈夫曼编码:
思想:得到哈夫曼树后,自顶向下按路径编号,指向左节点的边编号0,指向右节点的边编号1,从根到叶节点的所有边上的0和1连接起来,就是叶子节点中字符的哈夫曼编码。
下图体现了哈夫曼编码的过程:
很晚了==拜拜。