目录
- 写在前面的
- 3594: [Scoi2014]方伯伯的玉米田
- Gym - 101350F Monkeying Around
- BZOJ2962: 序列操作
- 51NOD 1672
- BZOJ3747: [POI2015]Kinoman
- D. 【普转提七联测 Day 3】DAG
- 校内模拟赛T3
- BZOJ4247 挂饰
- bzoj 5124: [Lydsy1712月赛]波浪序列
- BZOJ 1003 [ZJOI2006]物流运输
- BZOJ1296 粉刷匠
- Codeforces314E
- BZOJ3709
- POJ3280
- POJ2955
- BZOJ1090
写在前面的
头文件:
#include
using namespace std;
#define gc getchar()
#define rep(i , x, y) for(int i = x;i <= y;++ i)
#define sep(i , x, y) for(int i = x;i >= y;-- i)
#define PII pair
#define fi first
#define se second
inline int gi() {
int x = 0,f = 1;char c = gc;
while(c < '0' || c > '9') {if(c == '-')f = -1;c = gc;}
while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = gc;}
return x * f;
} 3594: [Scoi2014]方伯伯的玉米田
首先有性质:若一个点被拔高,则后面点都被拔高是最优的。
设\(f[i][j]\)表示以第i个位置结尾用掉了j次机会的最长序列
\[f[i][j]=max(f[k][l]|k
后面柿子可以用二维树状数组维护。
Gym - 101350F Monkeying Around
题目大意:给定若干(Li, Ri, Ki)表示Li到Ri的人都得到一个标号为ki的球,依次进行。n个人每个人有一个状态0或者1,如果在这次操作前已经有过ki这种球了,那么状态会变成0,否则变成1.初始的时候都是0.求m次操作后有多少个0.
从后往前区间覆盖,然后差分分类讨论check。
BZOJ2962: 序列操作
好久以前看到了,就是不会做,今天终于想出了一半还是没做出来。
用线段树维护序列,每个节点维护\(f[x]\),其中\(f[x]\)表示表示区间选x个数字的答案
更新: (fa)f[x] = (lson)f[i] * (rson)f[i - x]
区间加:考虑值\(a_k*a_{k+1}*a_{k + 2}....\) 变成\((a_k + c)*(a_{k+1} + c)*(a_{k + 2})....\)
dp[p]*v^(k-p)对dp[k]有影响
区间取反只考虑f值的奇偶性
51NOD 1672
交集是区间。从小到大枚举答案的左端点,并且使得答案被至少k个区间覆盖。
然后暴力枚举r在哪,会发现r是单调的。
所以用树状数组维护二维偏序直接上就OK.
BZOJ3747: [POI2015]Kinoman
裸数点问题吧,明天再补
D. 【普转提七联测 Day 3】DAG
可以证明的是,最长路=最小染色数-1
证明思路:证明对于一个染色方案,最长路\(≦\)染色数-1
进而证明对于一个最长路,能构造出一个合法染色方案
所以最长路=最小染色数-1
最小染色数=最小独立集
代码:
rep(i , 0, (1 << n) - 1) {
ind[i] = 1;
for(int j = 1;j <= m;++ j) {
if((i & (1 << u[j] - 1) ) && (i & (1 << v[j] - 1))) {
ind[i] = 0;
break;
}
}
}
f[0] = 0;
for(int i = 1;i < (1 << n);++ i) {
for(int s = i;s;s = (s - 1) & i) {
if(!ind[s]) continue;
f[i] = min(f[i] , f[s ^ i] + 1);
}
}校内模拟赛T3
求一个生成树使得上面只有k条边被标号,且和最小
结论题?
二分一个值,然后使得所有被标号的边-mid,然后进行最小生成树。
BZOJ4247 挂饰
贪心的想,\(b_i\)在上面越优,然后按照\(b_i\)排序
设\(f[i][j]\)表示前i个挂饰还有j个挂钩的最大价值。
类似于背包的转移
const int maxN = 2e3 + 7;
struct Node{
int a , b;
}a[maxN];
int f[maxN][maxN];
bool cmp(Node a, Node b) {
return a.a > b.a;
}
signed main() {
int n = gi();
rep(i , 1, n) {
a[i].a = gi();
a[i].b = gi();
}
sort(a + 1,a + n + 1, cmp);
int ans = 0;
memset(f,-0x3f,sizeof(f));
f[0][1] = 0;
rep(i , 1, n) {
rep(j , 0, n) {
f[i][j] = max(f[i - 1][j] , f[i - 1][max(j - a[i].a , 0LL) + 1] + a[i].b);
}
}
for(int i = 0;i <= n;++ i) ans = max(ans , f[n][i]);
printf("%lld",ans);
return 0;
}
/*
5
0 4
2 -2
1 -1
0 1
0 3
*/bzoj 5124: [Lydsy1712月赛]波浪序列
BZOJ 1003 [ZJOI2006]物流运输
有m个码头和e条航线,每天航线有成本。有连续n天需要从1号码头到m
号码头运输货物。每个码头会在某些天数区间内不许经过。每更换一次
运输路线,要付出k的成本。
◦求这n天的最小总成本。
◦m<=20,n<=100
这道题太棒了
只想到了一半\(/dk\)
可以想到对于路径都是一段一段的。
然后设\(f_i\)表示时间为i的最小价值
从j转移表示时间(j,i]都是相同的路径
则\(f_i = min(f_j + (i - j) * w(1,n)) + k\)
显然这里的\(w(1,n)\)是最短路。
我们把在(i,j]的区间的点都加入图,然后跑dij.
复杂度:\(n^2 * (m * logm)\)
const int maxM = 1e5 + 7;
const int maxN = 10000 + 7;
const int inf = 1000000000;
struct Node{
int v , nex, w;
}Map[maxM];
int head[maxN] , num;
void add_Node(int u , int v, int w) {
Map[++ num] = (Node) {v , head[u], w};
head[u] = num;
}
PII a[maxN];
int b[maxN];
int f[maxN],d;
int n, m, k, e;
bool vis[maxN],v[maxN];
int dis[maxN];
queue q;
bool ok[1001][1001];
int cost(int l , int r) {
rep(i , 1, m) dis[i] = inf , v[i] = 0,vis[i] = true;
rep(i , 1, d) {
rep(j , l ,r) {
if(ok[b[i]][j]) {
vis[b[i]] = false;
break;
}
}
}
q.push(1);
dis[1] = 0;v[1] = 1;
while(!q.empty()) {
int now = q.front();q.pop();
v[now] = 0;
for(int i = head[now];i;i = Map[i].nex) {
int y = Map[i].v;
if(!vis[y]) continue;
if(dis[y] > dis[now] + Map[i].w) {
dis[Map[i].v] = dis[now] + Map[i].w;
if(!v[y]) {
v[y] = true;
q.push(y);
}
}
}
}
if(dis[m] == inf) return inf;
return dis[m] * (r - l + 1);
}
int main() {
memset(f , 0x3f, sizeof(f));
n = gi() , m = gi(), k = gi(), e = gi();
while(e --) {
int u = gi() , v = gi(), w = gi();
add_Node(u , v, w);
add_Node(v , u, w);
}
f[0] = 0;
d = gi();
for(int i = 1;i <= d;++ i) {
b[i] = gi(); int t1 = gi() , t2 = gi();
rep(j , t1, t2) ok[b[i]][j] = true;
}
rep(i , 1, n) {
f[i] = cost(1 , i);
rep(j , 1, i - 1) {
f[i] = min(f[j] + cost(j + 1, i) + k ,f[i]);
}
}
printf("%d",f[n]);
return 0;
} BZOJ1296 粉刷匠
有n条木板要被粉刷,每条木板分为m个格子,每个格子需要被刷成蓝色
或红色。
◦每次粉刷可以在一条木板上给连续的一段格子刷上相同的颜色。每个格
子最多被刷一次。
◦问若只能刷k次,最多正确粉刷多少格子。
的确做出来了,
设\(f_{i,j}\)表示前i个格子用j次刷板机会的最多正确染色数。
\(f_{i,j} = max(f_{k,j- 1} + w(k + 1,i))(k是与i在同一木板的格子)\)
\(w(i,j)\)表示区间\([i,j]\)出现最多的颜色。
这样转移是\(n^3\)的.
优化:
\(g{i,j}\)表示第i个木板用了\(j\)次刷板机会的最大值。
Codeforces314E
给定一个长度为n的仅包含左右括号和问号的字符串,将问号变成左括号
或右括号使得该括号序列合法,求方案总数。
◦例如(())与()()都是合法的括号序列。
◦n<=3000。
括号问题转化:把左括号看成\((\),右括号看成\()\),是一个括号序列的条件是,满足任意的前缀和都\(>=0\)
这样就可以序列DP了
\(f_{i,j}\)表示前i个位置,和为\(j\)的方案数
当i+1是\((\)时,\(f_{i,j}\)转移到\(f_{i,j + 1}\)
当i+1是\()\)时,\(f_{i,j}\)转移到\(f_{i,j -1}\)
当i+1是\(?\)时,\(f_{i,j}\)转移到\(f_{i,j -1}\)和\(f_{i,j + 1}\)
转移就是加和
最后\(f_{n,0}\)就是答案
BZOJ3709
在一款电脑游戏中,你需要打败n只怪物(从1到n编号)。为了打败第i只怪物,你需要消耗d[i]点生命值,但怪物死后会掉落血药,使你恢复a[i]点生命值。任何时候你的生命值都不能降到0(或0以下)。请问是否存在一种打怪顺序,使得你可以打完这n只怪物而不死掉
很经典的贪心了。
按照\(a_i - d_i\)是否\(>=0\)分类
若\(a_i - d_i >=0\),则按照\(d_i\)排序,依次打怪。
若\(a_i - d_i <0\),我们考虑最后的值是一个定值,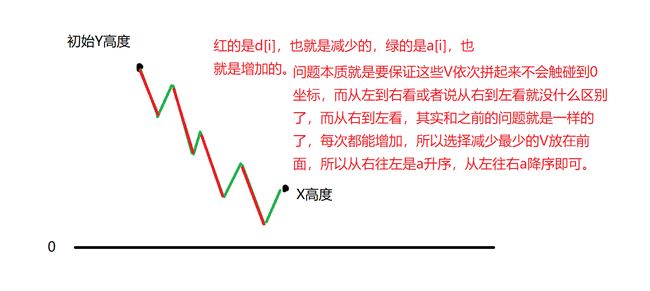
POJ3280
给你长度为m的字符串,其中有n种字符,每种字符都有两个值,分别是
插入这个字符的代价,删除这个字符的代价,让你求将原先给出的那串
字符变成一个回文串的最小代价。
◦M<=2000
区间DP,设\(f_{i,j}\)表示区间成为一个回文串的最小代价。
转移有三种。
POJ2955
给你一串()[]括号,要你求出这串括号的最大匹配个数,如'('与')'匹配,为
2个,'['与']'匹配,为2个,其他不能匹配.......
◦允许有杂质即( [ ( [ ] ] ) ] 应该是 [ ( [ ] ) ]//去掉杂质
◦就是选出一个最长合法子括号序列。
◦序列的长度小于等于100。
完美的括号序列条件:
1.空序列是一个完美的括号序列
2.若[l+1,r-1]是完美括号序列,且l和r能配对,则[l,r]也是完美的括号序列
3.两个并排的完美括号序列是一个完美的括号序列。
区间DP,\(f_{i,j}\)表示区间最长合法自括号的序列
和上道题一样,仍然考虑添加首位那个对状态什么影响。
若首位不被作为答案计入:\(f_{i,j} = f_{i,j - 1}\)
若首位作为答案计入:然后查找i+1~~j有木有与第i个括号匹配的。
BZOJ1090
折叠的定义如下: 1. 一个字符串可以看成它自身的折叠。记作S S 2. X(S)是X(X>1)个S连接在一起的串的折叠。记作X(S) SSSS…S(X个S)。 3. 如果A A’, BB’,则AB A’B’ 例如,因为3(A) = AAA, 2(B) = BB,所以3(A)C2(B) AAACBB,而2(3(A)C)2(B)AAACAAACBB 给一个字符串,求它的最短折叠。例如AAAAAAAAAABABABCCD的最短折叠为:9(A)3(AB)CCD。
字符串长度\(\ls 100\)
解法:
考虑序列DP,设\(f_i\)表示1~i区间最短的折叠。
但是有一个地方无法处理,即从\(f_j\)转移时,处理区间\([j + 1,i]\)字符串的最小循环节复杂度有点大(哈希+调和级数\(n log n\))
考虑区间DP,设\(f_{i,j}\)表示区间[i,j]最小折叠。