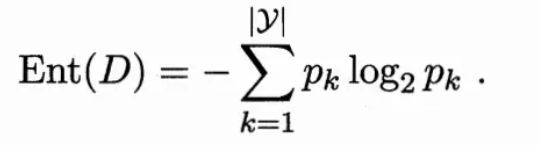关键字
信息增益:是特征选择中的一个重要指标,它定义为一个特征能够为分类系统带来多少信息,带来的信息越多,该特征越重要。
熵:那么如何衡量一个特征为分类系统带来的信息多少呢:对一个特征而言,系统有它和没它时信息量将发生变化,而前后信息量的差值就是这个特征给系统带来的信息量。所谓信息量,其实就是熵。信息熵可以衡量事物的不确定性,这个事物不确定性越大,信息熵也越大。
基尼指数:Gini是从数据集随机抽两个样本,不一致的概率。如果Gini越小,则数据集纯度越高。
剪枝处理:解决 “过拟合”的主要手段。有关“过拟合”(数据集匹配的太好)和“欠拟合”(数据集匹配的不好)之间的关系:http://www.cnblogs.com/nxld/p/6058782.html
分为: 预剪枝和 后剪枝
1、决策树的概念
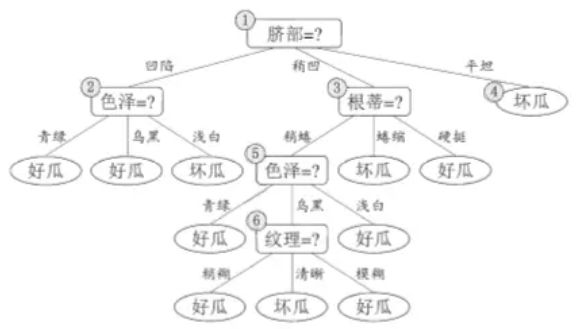
在机器学习中,决策树是一个预测模型,代表的是对象属性与对象值之间的一种映射关系。决策树是基于树结构来进行决策的。例如在西瓜问题中,对新样本的分类可看作对“当前样本属于正类吗”这个问题的“决策”过程。图4.1是西瓜问题的一棵决策树。
Entropy = 系统的凌乱程度,使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念。
C4.5算法是ID3算法的一个改进算法,在连续数值和不完整数值的吃力上都有了较好的改进。C4.5算法和ID3算法都最好在小数据集上使用,决策树分类一般只试用于小数据。当属性取值很多时最好选择C4.5算法,ID3得出的效果会非常差。而C5.0算法则是C4.5算法的修订版,适用于处理大数据集,采用Boosting方式提高模型准确率,又称为BoostingTrees,在软件上计算速度比较快,占用的内存资源较少。具体优缺点参考博客
2.决策树学习基本算法
从图中可以看到,决策树生成是一个递归过程。
有三种情形导致递归返回:1、当前结点包含的样本全属于同一类别,无需划分 2、当前属性集为空,或是所有样本在所有属性上取值相同,无法划分 3、当前结点包含的样本集合为空,不能划分。在第2种情形下,把当前结点标记为叶结点,但类别设定为该结点所含样本最多的类别。在第3种情形下,把当前结点标记为叶节点,但类别设定为其父结点所含样本最多的类别。它们的不同点是 ,第2种是利用当前结点的后验分布,第3种则是把父结点的样本分布作为当前结点的先验分布。
3.创建数据集和属性集合
用周志华老师西瓜数据集为例,创建西瓜的样式数据和色泽等属性集。
def createDataSet1(): # 创造数据集
dataSet = [['青绿' , '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
['乌黑' , '蜷缩' , '沉闷' , '清晰' , '凹陷' , '硬滑' , '好瓜'] ,
['乌黑' , '蜷缩' , '浊响' , '清晰' , '凹陷' , '硬滑' , '好瓜'] ,
['青绿' , '蜷缩' , '沉闷' , '清晰' , '凹陷' , '硬滑' , '好瓜'] ,
['浅白' , '蜷缩' , '浊响' , '清晰' , '凹陷' , '硬滑' , '好瓜'] ,
['青绿' , '稍缩' , '浊响' , '清晰' , '稍凹' , '软粘' , '好瓜'] ,
['乌黑' , '稍缩' , '浊响' , '稍糊' , '稍凹' , '软粘' , '好瓜'] ,
['乌黑' , '稍缩' , '浊响' , '清晰' , '稍凹' , '硬滑' , '好瓜'] ,
['乌黑' , '稍缩' , '沉闷' , '稍糊' , '稍凹' , '硬滑' , '好瓜'] ,
['青绿' , '硬挺' , '清脆' , '清晰' , '平坦' , '硬滑' , '坏瓜'] ,
['浅白' , '硬挺' , '清脆' , '模糊' , '平坦' , '软粘' , '坏瓜'] ,
['浅白' , '蜷缩' , '浊响' , '模糊' , '平坦' , '硬滑' , '坏瓜'] ,
['青绿' , '稍缩' , '浊响' , '稍糊' , '凹陷' , '软粘' , '坏瓜'] ,
['浅白' , '稍缩' , '沉闷' , '稍糊' , '凹陷' , '硬滑' , '坏瓜'] ,
['乌黑' , '稍缩' , '浊响' , '清晰' , '稍凹' , '软粘' , '坏瓜'] ,
['浅白' , '蜷缩' , '浊响' , '模糊' , '平坦' , '硬滑' , '坏瓜'] ,
['青绿' , '蜷缩' , '沉闷' , '稍糊' , '稍凹' , '硬滑' , '坏瓜'] ]
labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感'] #6个特征
return dataSet,labels
决策树的叶结点对应于决策结果,其他结点则对应于一个属性测试。
决策树学习的目的是为了产生一颗泛化能力强,即处理未见示例能力强的决策树,其基本流程遵循简单且直观的‘分而治之’策略。
4.计算数据划分属性方法
在决策树学习算法中,最重要的是选择最优划分属性。一般而言,随着划分过程不断进行,决策树的分支结点所包含的样本尽可能属于同一类别,即结点的‘纯度’越高越好。
为了度量样本纯度,在这里引入了‘信息熵’这个指标。
用熵来表示信息的复杂度,熵越大,则信息越复杂。公式如下:
假设有8个西瓜,3个好瓜,5个坏瓜。用色泽和触感这两个特征来判断是好瓜还是坏瓜。那么是先判断色泽好还是先触感好呢?需要通过计算比较两种信息增益的值更大,意味着用这个属性来进行划分所获得的“纯度提升”越大。过程如下:
正例占p1=5/8,反例占p2=3/8。
首先计算根节点的熵 :熵(总)=-5/8log2(5/8)-3/8log2(3/8)=0.9544
先按A色泽分类,分类后的结果为:青绿中有2好瓜2坏瓜。乌黑中有1好瓜3坏瓜。
熵(A青绿)=-2/4log2(2/4)-2/4log2(2/4)=1
熵(A乌黑)=-1/4log2(1/4)-3/4log2(3/4)=0.8113
熵(A)=4/8*0.8113+4/8*1=0.9057
信息增益(A)=熵(总)-熵(A)=0.9544-0.9057=0.0487
再按B触感分类,分类后的结果为:硬滑中有3好瓜3坏瓜。软粘中有0好瓜2坏瓜。
熵(B硬滑)=-3/6log2(3/6)-3/6log2(3/6)=1
熵(B软粘)=-2/2log2(2/2)=0
熵(B)=6/8*1+2/8*0=0.75
信息增益(B)=熵(总)-熵(B)=0.9544-0.75=0.2087
按B的方法,先按触感特征分类,信息增益更大,区分样本的能力更强,更具有代表性。
以下代码实现每一个特征的熵的计算
def calcShannonEnt(dataSet): # 计算数据的熵(entropy)
numEntries=len(dataSet) # 数据条数
labelCounts={}
for featVec in dataSet:
currentLabel=featVec[-1] # 每行数据的最后一个字(类别)
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1 # 统计有多少个类以及每个类的数量
shannonEnt=0 # 类的熵值
for key in labelCounts:
prob=float(labelCounts[key])/numEntries # 计算单个类的熵值
shannonEnt-=prob*log(prob,2) # 累加每个类的熵值
return shannonEnt
5、剪枝
剪枝是决策树算法处理“过拟合”的手段。剪枝的基本策略有“预剪枝”和“后剪枝”。预剪枝是对每个结点在划分前先进行估计,若当前结点的划分不能使决策树泛化性能提升,则停止划分并将当前结点标记为叶节点。后剪枝是先从训练集生成一棵完整的决策树,然后自底向上对非叶结点考察,若将该结点的子树替换成叶结点能使决策树性能提升,则将该子树替换成叶结点。
在这里,基于信息熵,我使用了“预剪枝”的策略。以脐部为例:
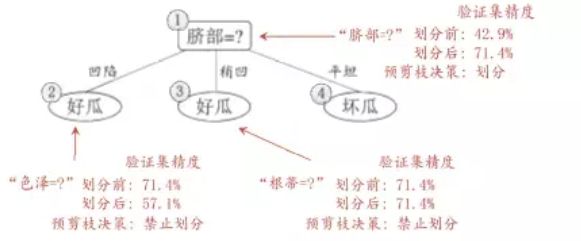
图5.1为未进行剪枝操作的生成的决策树,图5.2为基于信息熵生成的预剪枝决策树。
基本精度可以从图5.1划分的决策树计算出,精度为42.9%,而通过算法,我们可以从多种属性比较,看到以“脐部”为头结点,精度提高到71.4%,而其他的属性,精度提高并没有属性‘脐部’高,所以第一步选取了‘脐部’为头结点,其他分支同理。如第二个枝叶,选取色泽,精度从71.4%降低到了57.1%,所以在预剪枝操作,这个枝叶被剪掉。而根蒂同理。
实现代码如下:
def chooseBestFeatureToSplit(dataSet): # 选择最优的分类特征
numFeatures = len(dataSet[0])-1
baseEntropy = calcShannonEnt(dataSet) # 原始的熵
bestInfoGain = 0 # 最优信息增益
bestFeature = -1 # 最优特征
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value)
prob =len(subDataSet)/float(len(dataSet))
newEntropy +=prob*calcShannonEnt(subDataSet) # 按特征分类后的熵
infoGain = baseEntropy - newEntropy # 原始熵与按特征分类后的熵的差值
if (infoGain>bestInfoGain): # 若按某特征划分后,熵值减少的最大,则次特征为最优分类特征
bestInfoGain=infoGain
bestFeature = i
return bestFeature
但是预剪枝基于"贪心”本质禁止这些分支剪开,所以给预剪枝决策树带来欠拟合的风险。
6、决策树完整代码
from math import log
import operator
def calcShannonEnt(dataSet): # 计算数据的熵(entropy)
numEntries=len(dataSet) # 数据条数
labelCounts={}
for featVec in dataSet:
currentLabel=featVec[-1] # 每行数据的最后一个字(类别)
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1 # 统计有多少个类以及每个类的数量
shannonEnt=0
for key in labelCounts:
prob=float(labelCounts[key])/numEntries # 计算单个类的熵值
shannonEnt-=prob*log(prob,2) # 累加每个类的熵值
return shannonEnt
def createDataSet1(): # 创造数据集
dataSet = [['青绿' , '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
['乌黑' , '蜷缩' , '沉闷' , '清晰' , '凹陷' , '硬滑' , '好瓜'] ,
['乌黑' , '蜷缩' , '浊响' , '清晰' , '凹陷' , '硬滑' , '好瓜'] ,
['青绿' , '蜷缩' , '沉闷' , '清晰' , '凹陷' , '硬滑' , '好瓜'] ,
['浅白' , '蜷缩' , '浊响' , '清晰' , '凹陷' , '硬滑' , '好瓜'] ,
['青绿' , '稍缩' , '浊响' , '清晰' , '稍凹' , '软粘' , '好瓜'] ,
['乌黑' , '稍缩' , '浊响' , '稍糊' , '稍凹' , '软粘' , '好瓜'] ,
['乌黑' , '稍缩' , '浊响' , '清晰' , '稍凹' , '硬滑' , '好瓜'] ,
['乌黑' , '稍缩' , '沉闷' , '稍糊' , '稍凹' , '硬滑' , '好瓜'] ,
['青绿' , '硬挺' , '清脆' , '清晰' , '平坦' , '硬滑' , '坏瓜'] ,
['浅白' , '硬挺' , '清脆' , '模糊' , '平坦' , '软粘' , '坏瓜'] ,
['浅白' , '蜷缩' , '浊响' , '模糊' , '平坦' , '硬滑' , '坏瓜'] ,
['青绿' , '稍缩' , '浊响' , '稍糊' , '凹陷' , '软粘' , '坏瓜'] ,
['浅白' , '稍缩' , '沉闷' , '稍糊' , '凹陷' , '硬滑' , '坏瓜'] ,
['乌黑' , '稍缩' , '浊响' , '清晰' , '稍凹' , '软粘' , '坏瓜'] ,
['浅白' , '蜷缩' , '浊响' , '模糊' , '平坦' , '硬滑' , '坏瓜'] ,
['青绿' , '蜷缩' , '沉闷' , '稍糊' , '稍凹' , '硬滑' , '坏瓜'] ]
labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感'] #6个特征
return dataSet,labels
def splitDataSet(dataSet,axis,value): # 按某个特征分类后的数据
retDataSet=[]
for featVec in dataSet:
if featVec[axis]==value:
reducedFeatVec =featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
def chooseBestFeatureToSplit(dataSet): # 选择最优的分类特征
numFeatures = len(dataSet[0])-1
baseEntropy = calcShannonEnt(dataSet) # 原始的熵
bestInfoGain = 0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value)
prob =len(subDataSet)/float(len(dataSet))
newEntropy +=prob*calcShannonEnt(subDataSet) # 按特征分类后的熵
infoGain = baseEntropy - newEntropy # 原始熵与按特征分类后的熵的差值
if (infoGain>bestInfoGain): # 若按某特征划分后,熵值减少的最大,则次特征为最优分类特征
bestInfoGain=infoGain
bestFeature = i
return bestFeature
def majorityCnt(classList): #按分类后类别数量排序,比如:最后分类为2好瓜1坏瓜,则判定为好瓜;
classCount={}
for vote in classList:
if vote not in classCount.keys():
classCount[vote]=0
classCount[vote]+=1
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
def createTree(dataSet,labels):
classList=[example[-1] for example in dataSet] # 类别:好瓜或坏瓜
if classList.count(classList[0])==len(classList):
return classList[0]
if len(dataSet[0])==1:
return majorityCnt(classList)
bestFeat=chooseBestFeatureToSplit(dataSet) #选择最优特征
bestFeatLabel=labels[bestFeat]
myTree={bestFeatLabel:{}} #分类结果以字典形式保存
del(labels[bestFeat])
featValues=[example[bestFeat] for example in dataSet]
uniqueVals=set(featValues)
for value in uniqueVals:
subLabels=labels[:]
myTree[bestFeatLabel][value]=createTree(splitDataSet\
(dataSet,bestFeat,value),subLabels)
return myTree
if __name__=='__main__':
dataSet, labels=createDataSet1() # 创造示列数据
print(createTree(dataSet, labels)) # 输出决策树模型结果
# 输出结果:
#{'脐部': {'平坦': '坏瓜', '凹陷': {'根蒂': {'稍缩': '坏瓜', '蜷缩': '好瓜'}},
# '稍凹': {'根蒂': {'稍缩': {'纹理': {'清#晰': {'色泽': {'青绿': '好瓜', '乌黑': {'触感': {'硬滑': '好瓜', '软粘': '坏瓜'}}}},
# '稍糊': '好瓜'}}, '蜷缩': '坏瓜'}}}}
结果图:
多变量决策树
相比于ID3、C4.5、CART这种单变量决策树(分支时只用一个属性),多变量决策树在分支时用的是多个属性的加权组合,来个直观的图(以下),这个是单变量决策树学习出来的划分边界,这些边界都是与坐标轴平行的,多变量决策树的划分边界是倾斜于坐标轴的。
算法分支(详情参见http://scikit-learn.org/stable/modules/tree.html)
ID3
选取能够得到最大信息增益(information gain)的特征为数据划分归类,直到全部划分结束而不对树的规模进行任何控制。
等树生成之后,执行后剪枝。
信息增益的潜在问题是,比如有一个数据集含有一个特征是日期或者ID,则该特征会得到最大的信息增益,但是显然在验证数据中不会得到任何的结果。C45的信息增益比就是解决这个问题的。
C45
选取能够得到最大信息增益率(information gain ratio)的特征来划分数据,并且像ID3一样执行后剪枝。
是ID3的后续版本并扩展了IDC的功能,比如特征数值允许连续,在分类的时候进行离散化。
信息增益率:
“Gain ratio takes number and size of branches into account when choosing an attribute, and corrects the information gain by taking the intrinsic information of a split into account (i.e. how much info do we need to tell which branch an instance belongs to).”
C50
这是最新的一个版本,是有许可的(proprietary license)。比之C45,减少了内存,使用更少的规则集,并且准确率更高。
CART
CART(Classification and Regression Trees)分类回归树,它使用基尼不纯度(Gini Impurity)来决定划分。Gini Impurity和information gain ratio的理解和区分在这里:
http://stats.stackexchange.com/questions/94886/what-is-the-relationship-between-the-gini-score-and-the-log-likelihood-ratio。
它和C45基本上是类似的算法,主要区别:1)它的叶节点不是具体的分类,而是是一个函数f(),该函数定义了在该条件下的回归函数。2)CART是二叉树,而不是多叉树。
总结表
最后以下文章对以上内容总结挺好的 http://www.cnblogs.com/bourneli/archive/2013/03/15/2961568.html
完整代码点击码云查看