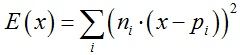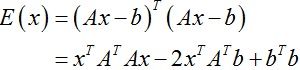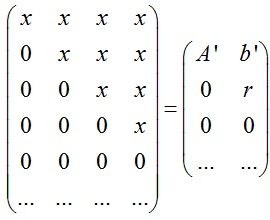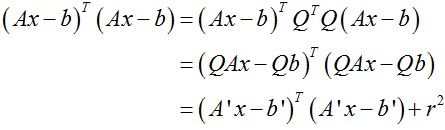上一篇介绍了Marching Cubes算法,Marching Cubes算法是三维重建算法中的经典算法,算法主要思想是检测与等值面相交的体素单元并计算交点的坐标,然后对不同的相交情况利用查找表在体素单元内构建相应的网格拓扑关系。Marching Cubes算法简单,但是存在一些缺陷:1.模型二义性问题;2.模型特征问题。
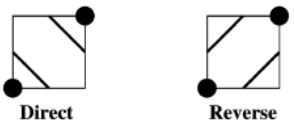
对于二义性问题,以2D情形为例,存在一个单元中同一顶点状态而不同的连接方式(如下图所示)。
图:2D中Marching Cubes算法的二义性问题
那么对于上图中两种连接方式的不同选择,可能会导致在同一张图像上完全不同的结果(如下图所示),二义性在3D中的直接后果是产生“孔洞”。如果在一个单元中,一条对角线的两端点值大于等值面阈值,另一条对角线的两端点值小于等值面阈值,那么通常会发生这种二义性问题。
图:二义性问题的不同结果
对于特征问题,由于Marching Cubes算法只计算体素单元的交点坐标信息,并根据这些交点连接的三角面片来构建体素单元内的几何模型,这样假如体素单元内存在几何模型的特征信息(棱边、棱角),但是Marching Cubes算法最终构建出的几何模型会缺少这些特征信息(如下图所示)。
图:左上-交点坐标和法向;右上-Marching Cubes算法;左下-Extended Marching Cubes算法;右下-Dual Contouring算法
Dual Contouring算法[Ju et al. 2002]也是经典的等值面提取算法,相比Marching Cubes算法,Dual Contouring算法利用Hermite数据(交点的位置和法向)进行等值面构建,它克服了Marching Cubes算法所出现的缺陷。具体算法分两步:
第一步:利用二次误差函数生成顶点坐标
对于每个与等值面相交的体素单元,通过最小化二次误差函数来生成一个顶点坐标:
其中pi为交点的位置,ni为交点的法向。
误差函数可以写成矩阵形式:
其中矩阵A的行向量为交点的法向ni,向量b的每个元素为ni·pi。
极值点可以通过求解正则方程得到:
![]()
但是文章指出这种方式会存在数值不稳定,并提出一种解决方法。基于QR矩阵分解计算正交矩阵Q,使得Q与[A b]相乘为如下上三角矩阵形式:
其中A'为3*3的上三角矩阵,b'为长度为3的向量,r为标量。
那么误差函数可以变化为:
然后再根据上式计算极值点。
第二步:生成网格面片
对于每一条等值面相交的体素边,那么包含该体素边的4个相邻体素单元内必然都存在顶点,将这4个顶点连接生成1个四边形面片。
文章[Schaefer et al. 2002]详细介绍了Dual Contouring算法的实现细节,通过总结该文可以得到Dual Contouring算法过程如下:
对于每个与等值面相交的体素单元:
1. 创建1个4*4的零矩阵用于存放QR矩阵分解的结果;
2. 对于体素单元的每条相交边,计算交点的位置pi和对应的法向ni;
3. 将向量[ ni.x, ni.y, ni.z, dot(pi,ni) ]添加到4*4的零矩阵底部;
4. 通过QR矩阵分解得到3*3的上三角矩阵A'和向量b';
5. 求解线性方程组A'TA'x = (A'Tb' - A'Tb'c) , 其中c是体素单元中所有交点的质心位置;
6. 将计算得到的偏移量x加上质心位置c即为体素单元中的顶点坐标;
7. 如果计算得到的顶点坐标位于体素单元之外,那么顶点坐标用质心位置c来代替;
8. 对于每一条相交的体素边,将其周围4个体素单元内的顶点连接生成1个四边形面片。
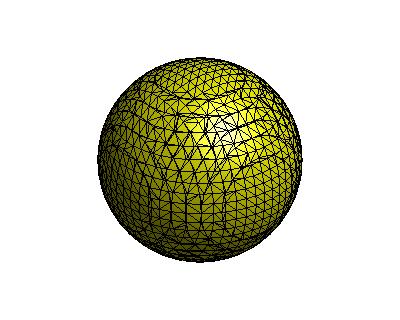
图:左- Marching Cubes算法;右-Dual Contouring算法
图:左- Marching Cubes算法;右-Dual Contouring算法
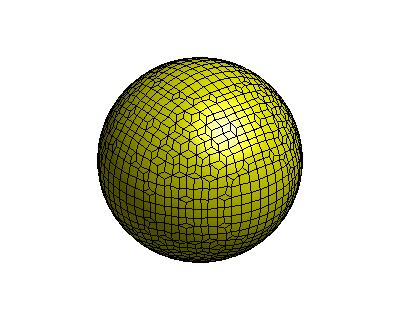
图:box与sphere相交模拟
本文为原创,转载请注明出处:http://www.cnblogs.com/shushen。
相关:
水泡动画模拟(Marching Cubes):http://www.cnblogs.com/shushen/p/5542131.html
参考文献:
[1] Tao Ju, Frank Losasso, Scott Schaefer, and Joe Warren. 2002. Dual contouring of hermite data. ACM Trans. Graph. 21, 3 (July 2002), 339-346.
[2] Scott Schaefer and Joe Warren. Dual contouring: The secret sauce. Technical Report 02-408, Department of Computer Science, Rice University, 2002.
[3] http://users.csc.calpoly.edu/~zwood/teaching/csc572/final15/kpidding/index.html