Deformable Convolutional Networks论文翻译——中文版

文章作者：Tyan
博客：noahsnail.com  |  CSDN  | 

声明：作者翻译论文仅为学习，如有侵权请联系作者删除博文，谢谢！

翻译论文汇总：https://github.com/SnailTyan/deep-learning-papers-translation

Deformable Convolutional Networks

摘要

卷积神经网络（CNN）由于其构建模块固定的几何结构天然地局限于建模几何变换。在这项工作中，我们引入了两个新的模块来提高CNN的转换建模能力，即可变形卷积和可变形RoI池化。两者都基于这样的想法：增加模块中的空间采样位置以及额外的偏移量，并且从目标任务中学习偏移量，而不需要额外的监督。新模块可以很容易地替换现有CNN中的普通模块，并且可以通过标准的反向传播便易地进行端对端训练，从而产生可变形卷积网络。大量的实验验证了我们方法的性能。我们首次证明了在深度CNN中学习密集空间变换对于复杂的视觉任务（如目标检测和语义分割）是有效的。代码发布在https://github.com/msracver/Deformable-ConvNets。

1. 引言

视觉识别中的一个关键挑战是如何在目标尺度，姿态，视点和部件变形中适应几何变化或建模几何变换。一般来说，有两种方法。首先是建立具有足够期望变化的训练数据集。这通常通过增加现有的数据样本来实现，例如通过仿射变换。鲁棒的表示可以从数据中学习，但是通常以昂贵的训练和复杂的模型参数为代价。其次是使用变换不变的特征和算法。这一类包含了许多众所周知的技术，如SIFT（尺度不变特征变换）[42]和基于滑动窗口的目标检测范例。

上述方法有两个缺点。首先，几何变换被假定是固定并且已知的。这样的先验知识被用来扩充数据，并设计特征和算法。这个假设阻止了对具有未知几何变换的新任务的泛化能力，这些新任务没有被正确地建模。其次，手工设计的不变特征和算法对于过于复杂的变换可能是困难的或不可行的，即使在已知复杂变化的情况下。

最近，卷积神经网络（CNNs）[35]在图像分类[31]，语义分割[41]和目标检测[16]等视觉识别任务中取得了显著的成功。不过，他们仍然有上述两个缺点。它们对几何变换建模的能力主要来自大量的数据增强，大的模型容量以及一些简单的手工设计模块（例如，对小的平移具有不变性的最大池化[1]）。

简而言之，CNN本质上局限于建模大型，未知的转换。该限制源于CNN模块的固定几何结构：卷积单元在固定位置对输入特征图进行采样；池化层以一个固定的比例降低空间分辨率；一个RoI（感兴趣区域）池化层把RoI分成固定的空间组块等等。缺乏处理几何变换的内部机制。这会导致明显的问题。举一个例子，同一CNN层中所有激活单元的感受野大小是相同的。对于在空间位置上编码语义的高级CNN层来说，这是不可取的。由于不同的位置可能对应不同尺度或形变的目标，所以对于具有精细定位的视觉识别来说，例如使用全卷积网络的语义分割[41]，尺度或感受野大小的自适应确定是理想的情况。又如，尽管最近目标检测已经取得了显著而迅速的进展[16,52,15,47,46,40,7]，但所有方法仍然依赖于基于特征提取的粗糙边界框。这显然是次优的，特别是对于非刚性目标。

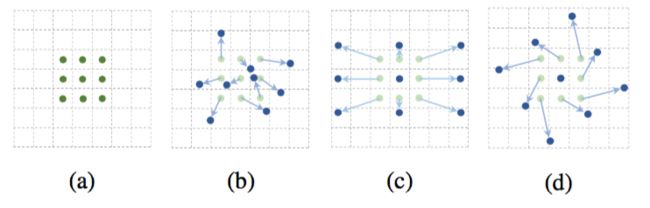
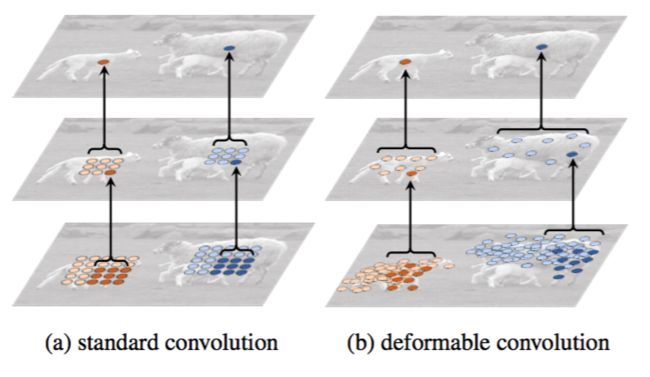
在这项工作中，我们引入了两个新的模块，大大提高了CNN建模几何变换的能力。首先是可变形卷积。它将2D偏移添加到标准卷积中的常规网格采样位置上。它可以使采样网格自由形变。如图1所示。偏移量通过附加的卷积层从前面的特征图中学习。因此，变形以局部的，密集的和自适应的方式受到输入特征的限制。

Figure 1

图1：3×3标准卷积和可变形卷积中采样位置的示意图。（a）标准卷积的定期采样网格（绿点）。（b）变形的采样位置（深蓝色点）和可变形卷积中增大的偏移量（浅蓝色箭头）。（c）（d）是（b）的特例，表明可变形卷积泛化到了各种尺度（各向异性）、长宽比和旋转的变换。

第二个是可变形的RoI池化。它为前面的RoI池化的常规bin分区中的每个bin位置添加一个偏移量[15,7]。类似地，从前面的特征映射和RoI中学习偏移量，使得具有不同形状的目标能够自适应的进行部件定位。

两个模块都轻量的。它们为偏移学习增加了少量的参数和计算。他们可以很容易地取代深层CNN中简单的对应部分，并且可以很容易地通过标准的反向传播进行端对端的训练。所得到的CNN被称为可变形卷积网络，或可变形ConvNets。

我们的方法与空间变换网络[26]和可变形部件模型[11]具有类似的高层精神。它们都有内部的转换参数，纯粹从数据中学习这些参数。可变形ConvNets的一个关键区别在于它们以简单，高效，深入和端到端的方式处理密集的空间变换。在3.1节中，我们详细讨论了我们的工作与以前的工作的关系，并分析了可变形ConvNets的优越性。

2. 可变形卷积网络

CNN中的特征映射和卷积是3D的。可变形卷积和RoI池化模块都在2D空间域上运行。在整个通道维度上的操作保持不变。在不丧失普遍性的情况下，为了符号清晰，这些模块在2D中描述。扩展到3D很简单。

2.1. 可变形卷积

2D卷积包含两步：1）用规则的网格$\mathcal{R}$在输入特征映射$\mathbf{x}$上采样；2）对$\mathbf{w}$加权的采样值求和。网格$\mathcal{R}$定义了感受野的大小和扩张。例如，$$\mathcal{R}=\lbrace (-1, -1), (-1, 0), \ldots, (0,1), (1, 1)\rbrace$$定义了一个扩张大小为$1$的$3 \times 3$卷积核。

对于输出特征映射$\mathbf{y}$上的每个位置$\mathbf{p}_0$，我们有$$\mathbf{y}(\mathbf{p}_0)=\sum_{\mathbf{p}_n\in\mathcal{R}}\mathbf{w}(\mathbf{p}_n)\cdot \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n) \tag{1}$$其中$\mathbf{p}_n$枚举了$\mathcal{R}$中的位置。

在可变形卷积中，规则的网格$\mathcal{R}$通过偏移$\lbrace \Delta \mathbf{p}_n|n=1,...,N\rbrace$增大，其中$N=|\mathcal{R}|$。方程(1)变为$$\mathbf{y}(\mathbf{p}_0)=\sum_{\mathbf{p}_n\in\mathcal{R}}\mathbf{w}(\mathbf{p}_n)\cdot \mathbf{x}(\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n).\tag{2}$$

现在，采样是在不规则且有偏移的位置$\mathbf{p}_n + \Delta \mathbf{p}_n$上。由于偏移$\Delta \mathbf{p}_n$通常是小数，方程(2)可以通过双线性插值实现$$\mathbf{x}(\mathbf{p})=\sum_\mathbf{q} G(\mathbf{q},\mathbf{p})\cdot \mathbf{x}(\mathbf{q}), \tag{3} $$其中$\mathbf{p}$表示任意（小数）位置(公式(2)中$\mathbf{p}=\mathbf{p}_0+\mathbf{p}_n+\Delta \mathbf{p}_n$)，$\mathbf{q}$枚举了特征映射$\mathbf{x}$中所有整体空间位置，$G(\cdot,\cdot)$是双线性插值的核。注意$G$是二维的。它被分为两个一维核$$ G(\mathbf{q},\mathbf{p})=g(q_x,p_x)\cdot g(q_y,p_y), \tag{4}$$其中$g(a,b)=max(0,1-|a-b|)$。方程(3)可以快速计算因为$G(\mathbf{q},\mathbf{p})$仅对于一些$\mathbf{q}$是非零的。

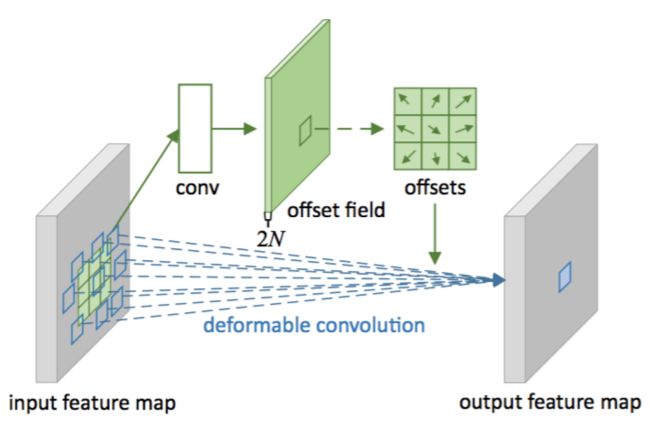
如图2所示，通过在相同的输入特征映射上应用卷积层来获得偏移。卷积核具有与当前卷积层相同的空间分辨率和扩张（例如，在图2中也具有扩张为1的$3\times 3$）。输出偏移域与输入特征映射具有相同的空间分辨率。通道维度$2N$对应于$N$个2D偏移量。在训练过程中，同时学习用于生成输出特征的卷积核和偏移量。为了学习偏移量，梯度通过方程(3)和(4)中的双线性运算进行反向传播。详见附录A。

Figure 2

图2：3×3可变形卷积的说明。

2.2. 可变形RoI池化

在所有基于区域提出的目标检测方法中都使用了RoI池化[16,15,47,7]。它将任意大小的输入矩形区域转换为固定大小的特征。

RoI池化[15]。给定输入特征映射$\mathbf{x}$、RoI的大小$w\times h$和左上角$\mathbf{p}_0$，RoI池化将ROI分到$k\times k$（$k$是一个自由参数）个组块(bin)中，并输出$k\times k$的特征映射$\mathbf{y}$。对于第$(i,j)$个组块($0\le i,j < k$)，我们有$$\mathbf{y}(i,j)=\sum_{\mathbf{p}\in bin(i,j)} \mathbf{x}(\mathbf{p}_0+\mathbf{p})/n_{ij},\tag{5}$$其中$n_{ij}$是组块中的像素数量。第$(i,j)$个组块的跨度为$\lfloor i \frac{w}{k} \rfloor \le p_x < \lceil (i+1)\frac{w}{k}\rceil$和$\lfloor j \frac{h}{k}\rfloor \le p_y < \lceil (j+1)\frac{h}{k} \rceil$。

类似于方程（2），在可变形RoI池化中，将偏移${\Delta \mathbf{p}_{ij}|0\le i,j < k}$加到空间组块的位置上。方程（5）变为$$\mathbf{y}(i,j)=\sum_{\mathbf{p}\in bin(i,j)} \mathbf{x}(\mathbf{p}_0+\mathbf{p}+\Delta \mathbf{p}_{ij})/n_{ij}. \tag{6}$$通常，$\Delta \mathbf{p}_{ij}$是小数。方程（6）通过双线性插值方程（3）和（4）来实现。

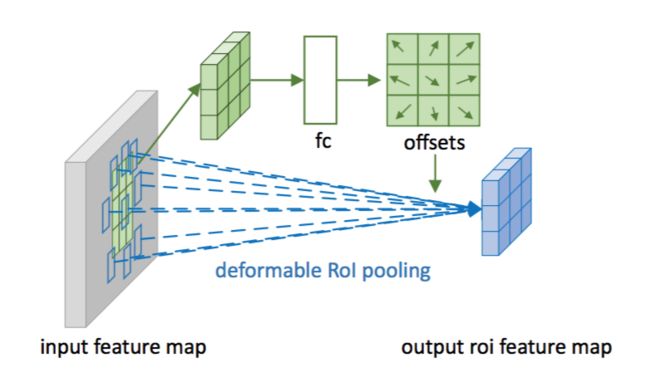
图3说明了如何获得偏移量。首先，RoI池化(方程(5))生成池化后的特征映射。从特征映射中，一个fc层产生归一化偏移量$\Delta \widehat{\mathbf{p}}_{ij}$，然后通过与RoI的宽和高进行逐元素的相乘将其转换为方程(6)中的偏移量$\Delta \mathbf{p}_{ij}$，如：$\Delta \mathbf{p}_{ij} = \gamma \cdot \Delta \widehat{\mathbf{p}}_{ij} \circ (w, h)$。这里$\gamma$是一个预定义的标量来调节偏移的大小。它经验地设定为$\gamma=0.1$。为了使偏移学习对RoI大小具有不变性，偏移归一化是必要的。fc层是通过反向传播学习，详见附录A。

Figure 3

图3：阐述3×3的可变形RoI池化。

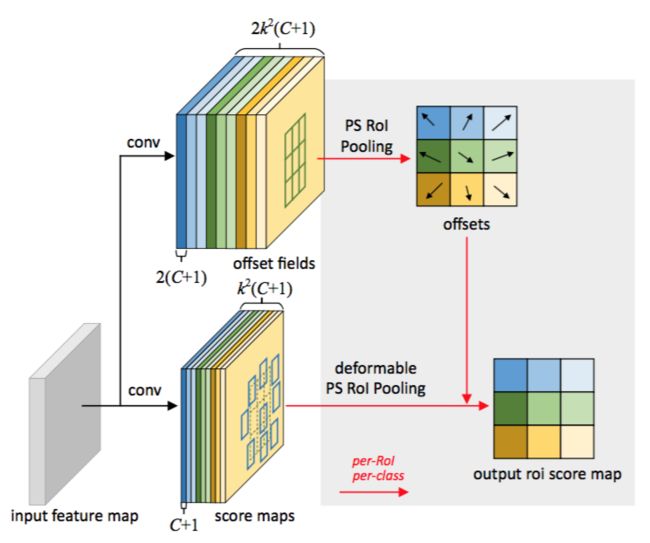
位置敏感（PS）的RoI池化[7]。它是全卷积的，不同于RoI池化。通过一个卷积层，所有的输入特征映射首先被转换为每个目标类的$k^2$个分数映射（对于$C$个目标类，总共$C+1$个），如图4的底部分支所示。不需要区分类，这样的分数映射被表示为$\lbrace \mathbf{x}_{i,j}\rbrace$，其中$(i,j)$枚举所有的组块。池化是在这些分数映射上进行的。第$(i,j)$个组块的输出值是通过对分数映射$\mathbf{x}_{i,j}$对应的组块求和得到的。简而言之，与方程（5）中RoI池化的区别在于，通用特征映射$\mathbf{x}$被特定的位置敏感的分数映射$\mathbf{x}_{i,j}$所取代。

Figure 4

图4：阐述3×3的可变形PS RoI池化。

在可变形PS RoI池化中，方程（6）中唯一的变化是$\mathbf{x}$也被修改为$\mathbf{x}_{i,j}$。但是，偏移学习是不同的。它遵循[7]中的“全卷积”精神，如图4所示。在顶部分支中，一个卷积层生成完整空间分辨率的偏移量字段。对于每个RoI（也对于每个类），在这些字段上应用PS RoI池化以获得归一化偏移量$\Delta \widehat{\mathbf{p}}_{ij}$，然后以上面可变形RoI池化中描述的相同方式将其转换为实数偏移量$\Delta \mathbf{p}_{ij}$。

2.3. 可变形卷积网络

可变形卷积和RoI池化模块都具有与普通版本相同的输入和输出。因此，它们可以很容易地取代现有CNN中的普通版本。在训练中，这些添加的用于偏移学习的conv和fc层的权重被初始化为零。它们的学习率设置为现有层学习速率的$\beta$倍（默认$\beta=1$，Faster R-CNN中的fc层为$\beta=0.01$）。它们通过方程（3）和方程（4）中双线性插值运算的反向传播进行训练。由此产生的CNN称为可变形ConvNets。

为了将可变形的ConvNets与最先进的CNN架构集成，我们注意到这些架构由两个阶段组成。首先，深度全卷积网络在整个输入图像上生成特征映射。其次，浅层任务专用网络从特征映射上生成结果。我们详细说明下面两个步骤。

特征提取的可变形卷积。我们采用两种最先进的架构进行特征提取：ResNet-101[22]和Inception-ResNet[51]的修改版本。两者都在ImageNet[8]分类数据集上进行预训练。

最初的Inception-ResNet是为图像识别而设计的。它有一个特征不对齐的问题，对于密集的预测任务是有问题的。它被修改来解决对齐问题[20]。修改后的版本被称为“Aligned-Inception-ResNet”，详见附录B.

两种模型都由几个卷积块组成，平均池化和用于ImageNet分类的1000类全连接层。平均池化和全连接层被移除。最后加入随机初始化的1×1卷积，以将通道维数减少到1024。与通常的做法[4,7]一样，最后一个卷积块的有效步长从32个像素减少到16个像素，以增加特征映射的分辨率。具体来说，在最后一个块的开始，步长从2变为1（ResNet-101和Aligned-Inception-ResNet的“conv5”）。为了进行补偿，将该块（核大小>1）中的所有卷积滤波器的扩张从1改变为2。

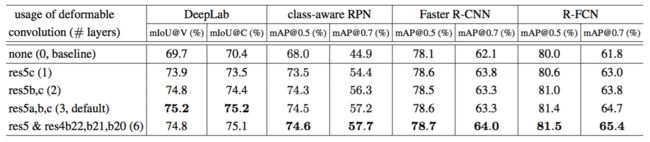
可选地，可变形卷积应用于最后的几个卷积层（核大小>1）。我们尝试了不同数量的这样的层，发现3是不同任务的一个很好的权衡，如表1所示。

Table 1

表1：在ResNet-101特征提取网络中的最后1个，2个，3个和6个卷积层上（3×3滤波器）应用可变形卷积的结果。对于class-aware RPN，Faster R-CNN和R-FCN，我们报告了在VOC 2007测试集上的结果。

分割和检测网络。根据上述特征提取网络的输出特征映射构建特定任务的网络。

在下面，$C$表示目标类别的数量。

DeepLab[5]是最先进的语义分割方法。它在特征映射上添加1×1卷积层以生成表示每个像素分类分数的（C+1）个映射。然后随后的softmax层输出每个像素的概率。

除了用（C+1）类卷积分类器代替2类（目标或非目标）卷积分类器外，Category-Aware RPN与[47]中的区域提出网络几乎是相同的。它可以被认为是SSD的简化版本[40]。

Faster R-CNN[47]是最先进的检测器。在我们的实现中，RPN分支被添加在conv4块的顶部，遵循[47]。在以前的实践中[22,24]，在ResNet-101的conv4和conv5块之间插入了RoI池化层，每个RoI留下了10层。这个设计实现了很好的精确度，但是具有很高的per-RoI计算。相反，我们采用[38]中的简化设计。RoI池化层在最后添加。在池化的RoI特征之上，添加了两个1024维的全连接层，接着是边界框回归和分类分支。虽然这样的简化（从10层conv5块到2个全连接层）会稍微降低精确度，但它仍然具有足够强的基准，在这项工作中不再关心。

可选地，可以将RoI池化层更改为可变形的RoI池化。

R-FCN[7]是另一种最先进的检测器。它的每个RoI计算成本可以忽略不计。我们遵循原来的实现。可选地，其RoI池化层可以改变为可变形的位置敏感的RoI池化。

3. 理解可变形卷积网络

这项工作以用额外的偏移量在卷积和RoI池中增加空间采样位置，并从目标任务中学习偏移量的想法为基础。

当可变形卷积叠加时，复合变形的影响是深远的。这在图5中举例说明。标准卷积中的感受野和采样位置在顶部特征映射上是固定的（左）。它们在可变形卷积中（右）根据目标的尺寸和形状进行自适应调整。图6中显示了更多的例子。表2提供了这种自适应变形的量化证据。

Figure 5

图5：标准卷积（a）中的固定感受野和可变形卷积（b）中的自适应感受野的图示，使用两层。顶部：顶部特征映射上的两个激活单元，在两个不同尺度和形状的目标上。激活来自3×3滤波器。中间：前一个特征映射上3×3滤波器的采样位置。另外两个激活单元突出显示。底部：前一个特征映射上两个3×3滤波器级别的采样位置。突出显示两组位置，对应于上面突出显示的单元。

Figure 6

图6：每个图像三元组在三级3×3可变形滤波器（参见图5作为参考）中显示了三个激活单元（绿色点）分别在背景（左）、小目标（中）和大目标（右）上的采样位置（每张图像中的$9^3 = 729$个红色点）。

Table 2

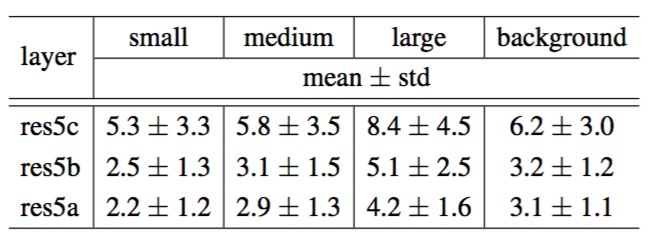
表2：可变形卷积滤波器在三个卷积层和四个类别上的有效扩张值的统计。与在COCO[39]中类似，我们根据边界框区域将目标平均分为三类。小：面积<$96^{2$个像素；中等：$96}2$<面积<$224^2$； 大：面积>$224^2$。

可变形RoI池化的效果是类似的，如图7所示。标准RoI池化中网格结构的规律不再成立。相反，部分偏离RoI组块并移动到附近的目标前景区域。定位能力得到增强，特别是对于非刚性物体。

Figure 7

图7：R-FCN[7]中可变形（正敏感）RoI池化的偏移部分的示意图和输入RoI（黄色）的3x3个组块（红色）。请注意部件如何偏移以覆盖非刚性物体。

3.1. 相关工作的背景

我们的工作与以前的工作在不同的方面有联系。我们详细讨论联系和差异。

空间变换网络（STN）[26]。这是在深度学习框架下从数据中学习空间变换的第一个工作。它通过全局参数变换扭曲特征映射，例如仿射变换。这种扭曲是昂贵的，学习变换参数是困难的。STN在小规模图像分类问题上取得了成功。反STN方法[37]通过有效的变换参数传播来代替昂贵的特征扭曲。

可变形卷积中的偏移学习可以被认为是STN中极轻的空间变换器[26]。然而，可变形卷积不采用全局参数变换和特征扭曲。相反，它以局部密集的方式对特征映射进行采样。为了生成新的特征映射，它有加权求和步骤，STN中不存在。

可变形卷积很容易集成到任何CNN架构中。它的训练很简单。对于要求密集（例如语义分割）或半密集（例如目标检测）预测的复杂视觉任务来说，它是有效的。这些任务对于STN来说是困难的（如果不是不可行的话）[26,37]。

主动卷积[27]。这项工作是当代的。它还通过偏移来增加卷积中的采样位置，并通过端到端的反向传播学习偏移量。它对于图像分类任务是有效的。

与可变形卷积的两个关键区别使得这个工作不那么一般和适应。首先，它在所有不同的空间位置上共享偏移量。其次，偏移量是每个任务或每次训练都要学习的静态模型参数。相反，可变形卷积中的偏移是每个图像位置变化的动态模型输出。他们对图像中的密集空间变换进行建模，对于（半）密集的预测任务（如目标检测和语义分割）是有效的。

有效的感受野[43]。它发现，并不是感受野中的所有像素都贡献平等的输出响应。中心附近的像素影响更大。有效感受野只占据理论感受野的一小部分，并具有高斯分布。虽然理论上的感受野大小随卷积层数量线性增加，但令人惊讶的结果是，有效感受野大小随着数量的平方根线性增加，因此，感受野大小以比我们期待的更低的速率增加。

这一发现表明，即使是深层CNN的顶层单元也可能没有足够大的感受野。这部分解释了为什么空洞卷积[23]被广泛用于视觉任务（见下文）。它表明了自适应感受野学习的必要。

空洞卷积[23]。它将正常滤波器的步长增加到大于1，并保持稀疏采样位置的原始权重。这增加了感受野的大小，并保持了相同的参数和计算复杂性。它已被广泛用于语义分割[41,5,54]（在[54]中也称扩张卷积），目标检测[7]和图像分类[55]。

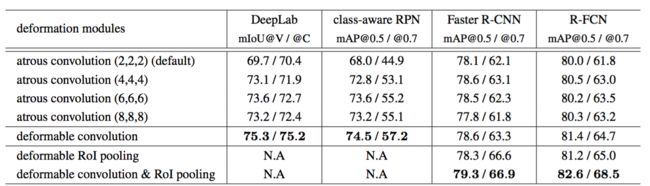
可变形卷积是空洞卷积的推广，如图1（c）所示。表3给出了大量的与空洞卷积的比较。

Table 3

表3：我们的可变形模块与空洞卷积的评估，使用ResNet-101。

可变形部件模型（DPM）[11]。可变形RoI池化与DPM类似，因为两种方法都可以学习目标部件的空间变形，以最大化分类得分。由于不考虑部件之间的空间关系，所以可变形RoI池化更简单。

DPM是一个浅层模型，其建模变形能力有限。虽然其推理算法可以通过将距离变换视为一个特殊的池化操作转换为CNN[17]，但是它的训练不是端到端的，而是涉及启发式选择，例如选择组件和部件尺寸。相比之下，可变形ConvNets是深层的并进行端到端的训练。当多个可变形模块堆叠时，建模变形的能力变得更强。

DeepID-Net[44]。它引入了一个变形约束池化层，它也考虑了目标检测的部分变形。因此，它与可变形RoI池化共享类似的精神，但是要复杂得多。这项工作是高度工程化并基于RCNN的[16]。目前尚不清楚如何以端对端的方式将其应用于最近的最先进目标检测方法[47,7]。

RoI池化中的空间操作。空间金字塔池化[34]在尺度上使用手工设计的池化区域。它是计算机视觉中的主要方法，也用于基于深度学习的目标检测[21,15]。

很少有学习池化区域空间布局的研究。[28]中的工作从一个大型的超完备集合中学习了池化区域一个稀疏子集。大数据集是手工设计的并且学习不是端到端的。

可变形RoI池化第一个在CNN中端到端地学习池化区域。虽然目前这些区域的规模相同，但像空间金字塔池化[34]那样扩展到多种尺度很简单。

变换不变特征及其学习。在设计变换不变特征方面已经进行了巨大的努力。值得注意的例子包括尺度不变特征变换（SIFT）[42]和ORB[49]（O为方向）。在CNN的背景下有大量这样的工作。CNN表示对图像变换的不变性和等价性在[36]中被研究。一些工作学习关于不同类型的变换（如[50]，散射网络[3]，卷积森林[32]和TI池化[33]）的不变CNN表示。有些工作专门用于对称性[13,9]，尺度[29]和旋转[53]等特定转换。

如第一部分分析的那样，在这些工作中，转换是先验的。使用知识（比如参数化）来手工设计特征提取算法的结构，或者是像SIFT那样固定的，或者用学习的参数，如基于CNN的那些。它们无法处理新任务中的未知变换。

相反，我们的可变形模块概括了各种转换（见图1）。从目标任务中学习变换的不变性。

动态滤波器[2]。与可变形卷积类似，动态滤波器也是依据输入特征并在采样上变化。不同的是，只学习滤波器权重，而不是像我们这样采样位置。这项工作适用于视频和立体声预测。

低级滤波器的组合。高斯滤波器及其平滑导数[30]被广泛用于提取低级图像结构，如角点，边缘，T形接点等。在某些条件下，这些滤波器形成一组基，并且它们的线性组合在同一组几何变换中形成新的滤波器，例如Steerable Filters[12]中的多个方向和[45]中多尺度。我们注意到尽管[45]中使用了可变形内核这个术语，但它的含义与我们在本文中的含义不同。

大多数CNN从零开始学习所有的卷积滤波器。最近的工作[25]表明，这可能是没必要的。它通过低阶滤波器（高斯导数达4阶）的加权组合来代替自由形式的滤波器，并学习权重系数。通过对滤波函数空间的正则化，可以提高训练小数据量时的泛化能力。

上面的工作与我们有关，当多个滤波器，尤其是不同尺度的滤波器组合时，所得到的滤波器可能具有复杂的权重，并且与我们的可变形卷积滤波器相似。但是，可变形卷积学习采样位置而不是滤波器权重。

4. 实验

4.1. 实验设置和实现

语义分割。我们使用PASCAL VOC[10]和CityScapes[6]。对于PASCAL VOC，有20个语义类别。遵循[19,41,4]中的协议，我们使用VOC 2012数据集和[18]中的附加掩模注释。训练集包含10,582张图像。评估在验证集中的1,449张图像上进行。对于CityScapes，按照[5]中的协议，对火车数据集中的2,975张图像和验证集中的500张图像分别进行训练和评估。有19个语义类别加上一个背景类别。

为了评估，我们使用在图像像素上定义的平均交集（mIoU）度量，遵循标准协议[10，6]。我们在PASCAl VOC和Cityscapes上分别使用mIoU@V和mIoU@C。

在训练和推断中，PASCAL VOC中图像的大小调整为较短边有$360$个像素，Cityscapes较短边有$1,024$个像素。在SGD训练中，每个小批次数据中每张图像进行随机采样。分别对PASCAL VOC和Cityscapes进行30k和45k迭代，有8个GPU每个GPU上处理一个小批次数据。前$\frac {2} {3}$次迭代的学习率为$10^{{-3}$，最后$\frac{1}{3}$次迭代学习率为$10}{-4}$。

目标检测。我们使用PASCAL VOC和COCO[39]数据集。对于PASCAL VOC，按照[15]中的协议，对VOC 2007 trainval和VOC 2012 trainval的并集进行培训。评估是在VOC 2007测试集上。对于COCO，遵循标准协议[39]，分别对trainval中的120k张图像和test-dev中的20k张图像进行训练和评估。

为了评估，我们使用标准的平均精度均值（MAP）得分[10,39]。对于PASCAL VOC，我们使用0.5和0.7的IoU阈值报告mAP分数。对于COCO，我们使用mAP@[0.5：0.95]的标准COCO度量，以及[email protected]。

在训练和推断中，图像被调整为较短边具有600像素。在SGD训练中，每个小批次中随机抽取一张图片。对于class-aware RPN，从图像中采样256个RoI。对于Faster R-CNN和R-FCN，对区域提出和目标检测网络分别采样256个和128个RoI。在ROI池化中采用$7\times 7$的组块。为了促进VOC的消融实验，我们遵循[38]，并且利用预训练的和固定的RPN提出来训练Faster R-CNN和R-FCN，而区域提出和目标检测网络之间没有特征共享。RPN网络是在[47]中过程的第一阶段单独训练的。对于COCO，执行[48]中的联合训练，并且训练可以进行特征共享。在8个GPU上分别对PASCAL VOC和COCO执行30k次和240k次迭代。前$\frac {2} {3}$次迭代和后$\frac{1}{3}$次迭代的学习率分别设为$10^{-3}$，$10{-4}$。

4.2. 消融研究

我们进行了广泛的消融研究来验证我们方法的功效性和有效性。

可变形卷积。表1使用ResNet-101特征提取网络评估可变形卷积的影响。当使用更多可变形卷积层时，精度稳步提高，特别是DeepLab和class-aware RPN。当DeepLab使用3个可变形层时，改进饱和，其它的使用6个。在其余的实验中，我们在特征提取网络中使用3个。

我们经验地观察到，可变形卷积层中学习到的偏移量对图像内容具有高度的自适应性，如图5和图6所示。为了更好地理解可变形卷积的机制，我们为可变形卷积滤波器定义了一个称为有效扩张的度量。它是滤波器中所有采样位置的相邻对之间距离的平均值。这是对滤波器的感受野大小的粗略测量。

我们在VOC 2007测试图像上应用R-FCN网络，具有3个可变形层（如表1所示）。根据真实边界框标注和滤波器中心的位置，我们将可变形卷积滤波器分为四类：小，中，大和背景。表2报告了有效扩张值的统计（平均值和标准差）。它清楚地表明：1）可变形滤波器的感受野大小与目标大小相关，表明变形是从图像内容中有效学习到的； 2）背景区域上的滤波器大小介于中，大目标的滤波器之间，表明一个相对较大的感受野是识别背景区域所必需的。这些观察结果在不同层上是一致的。

默认的ResNet-101模型在最后的3个3×3卷积层使用扩张为的2空洞卷积（见2.3节）。我们进一步尝试了扩张值4，6和8，并在表3中报告了结果。它表明：1）当使用较大的扩张值时，所有任务的准确度都会增加，表明默认网络的感受野太小；* 2）对于不同的任务，最佳扩张值是不同的，例如，6用于DeepLab，4用于Faster R-CNN； 3）可变形卷积具有最好的精度。这些观察结果证明了滤波器变形的自适应学习是有效和必要的。

可变形RoI池化。它适用于Faster R-CNN和R-FCN。如表3所示，单独使用它已经产生了显著的性能收益，特别是在严格的[email protected]度量标准下。当同时使用可变形卷积和RoI池化时，会获得显著准确性改进。

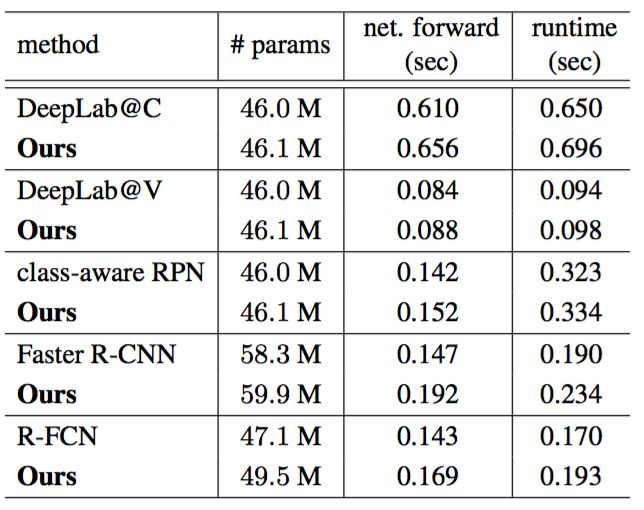
模型复杂性和运行时间。表4报告了所提出的可变形ConvNets及其普通版本的模型复杂度和运行时间。可变形ConvNets仅增加了很小的模型参数和计算量。这表明显著的性能改进来自于建模几何变换的能力，而不是增加模型参数。

Table 4

表4：使用ResNet-101的可变形ConvNets和对应普通版本的模型复杂性和运行时比较。最后一列中的整体运行时间包括图像大小调整，网络前馈传播和后处理（例如，用于目标检测的NMS）。运行时间计算是在一台配备了Intel E5-2650 v2 CPU和Nvidia K40 GPU的工作站上。

4.3. COCO的目标检测

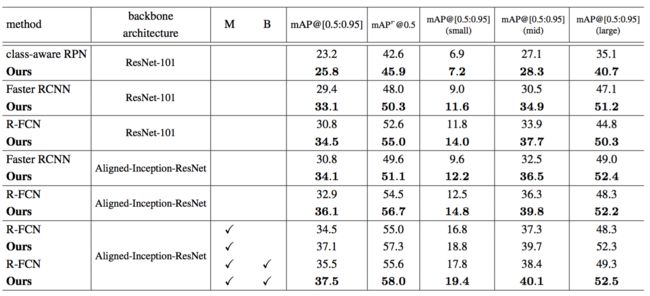
在表5中，我们在COCO test-dev数据集上对用于目标检测的可变形ConvNets和普通ConvNets进行了广泛的比较。我们首先使用ResNet-101模型进行实验。class-aware RPN，Faster CNN和R-FCN的可变形版本分别获得了$25.8%$，$33.1%$和$34.5%$的mAP@[0.5：0.95]分数，分别比它们对应的普通ConvNets相对高了$11%$，$13%$和$12%$。通过在Faster R-CNN和R-FCN中用Aligned-Inception-ResNet取代ResNet-101，由于更强大的特征表示，它们的普通ConvNet基线都得到了提高。而可变形ConvNets带来的有效性能收益也是成立的。通过在多个图像尺度上（图像较短边在[480,576,688,864,1200,1400]内）的进一步测试，并执行迭代边界框平均[14]，对于R-FCN的可变形版本，mAP@[0.5：0.95]分数增加到了37.5％。请注意，可变形ConvNets的性能增益是对这些附加功能的补充。

Table 5

表5：可变形ConvNets和普通ConvNets在COCO test-dev数据集上的目标检测结果。在表中M表示多尺度测试，B表示迭代边界框平均值。

5. 结论

本文提出了可变形ConvNets，它是一个简单，高效，深度，端到端的建模密集空间变换的解决方案。我们首次证明了在CNN中学习高级视觉任务（如目标检测和语义分割）中的密集空间变换是可行和有效的。

致谢

Aligned-Inception-ResNet模型由Kaiming He，Xiangyu Zhang，Shaoqing Ren和Jian Sun在未发表的工作中进行了研究和训练。

References

[1] Y.-L. Boureau, J. Ponce, and Y. LeCun. A theoretical analysis of feature pooling in visual recognition. In ICML, 2010. 1

[2] B. D. Brabandere, X. Jia, T. Tuytelaars, and L. V. Gool. Dynamic filter networks. In NIPS, 2016. 6

[3] J. Bruna and S. Mallat. Invariant scattering convolution networks. TPAMI, 2013. 6

[4] L.-C. Chen, G. Papandreou, I. Kokkinos, K. Murphy, and A. L. Yuille. Semantic image segmentation with deep convolutional nets and fully connected crfs. In ICLR, 2015. 4, 7

[5] L.-C. Chen, G. Papandreou, I. Kokkinos, K. Murphy, and A. L. Yuille. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. arXiv preprint arXiv:1606.00915, 2016. 4, 6, 7

[6] M. Cordts, M. Omran, S. Ramos, T. Rehfeld, M. Enzweiler, R. Benenson, U. Franke, S. Roth, and B. Schiele. The cityscapes dataset for semantic urban scene understanding. In CVPR, 2016. 7

[7] J. Dai, Y. Li, K. He, and J. Sun. R-fcn: Object detection via region-based fully convolutional networks. In NIPS, 2016. 1, 2, 3, 4, 5, 6

[8] J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, and L. Fei-Fei. Imagenet: A large-scale hierarchical image database. In CVPR, 2009. 4, 10

[9] S. Dieleman, J. D. Fauw, and K. Kavukcuoglu. Exploiting cyclic symmetry in convolutional neural networks. arXiv preprint arXiv:1602.02660, 2016. 6

[10] M. Everingham, L. Van Gool, C. K. Williams, J. Winn, and A. Zisserman. The PASCAL Visual Object Classes (VOC) Challenge. IJCV, 2010. 7

[11] P. F. Felzenszwalb, R. B. Girshick, D. McAllester, and D. Ramanan. Object detection with discriminatively trained part-based models. TPAMI, 2010. 2, 6

[12] W. T. Freeman and E. H. Adelson. The design and use of steerable filters. TPAMI, 1991. 6

[13] R. Gens and P. M. Domingos. Deep symmetry networks. In NIPS, 2014. 6

[14] S. Gidaris and N. Komodakis. Object detection via a multiregion & semantic segmentation-aware cnn model. In ICCV, 2015. 9

[15] R. Girshick. Fast R-CNN. In ICCV, 2015. 1, 2, 3, 6, 7

[16] R. Girshick, J. Donahue, T. Darrell, and J. Malik. Rich feature hierarchies for accurate object detection and semantic segmentation. In CVPR, 2014. 1, 3, 6

[17] R. Girshick, F. Iandola, T. Darrell, and J. Malik. Deformable part models are convolutional neural networks.

[20] K. He, X. Zhang, S. Ren, and J. Sun. Aligned-inceptionresnet model, unpublished work. 4, 10

[21] K. He, X. Zhang, S. Ren, and J. Sun. Spatial pyramid pooling in deep convolutional networks for visual recognition. In ECCV, 2014. 6

[22] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In CVPR, 2016. 4, 10

[23] M. Holschneider, R. Kronland-Martinet, J. Morlet, and P. Tchamitchian. A real-time algorithm for signal analysis with the help of the wavelet transform. Wavelets: Time-Frequency Methods and Phase Space, page 289297, 1989. 6

[24] J. Huang, V. Rathod, C. Sun, M. Zhu, A. Korattikara, A. Fathi, I. Fischer, Z. Wojna, Y. Song, S. Guadarrama, and K. Murphy. Speed/accuracy trade-offs for modern convolutional object detectors. arXiv preprint arXiv:1611.10012, 2016. 4

[25] J.-H. Jacobsen, J. van Gemert, Z. Lou, and A. W.M.Smeulders. Structured receptive fields in cnns. In CVPR, 2016. 6

[26] M. Jaderberg, K. Simonyan, A. Zisserman, and K. Kavukcuoglu. Spatial transformer networks. In NIPS, 2015. 2, 5

[27] Y. Jeon and J. Kim. Active convolution: Learning the shape of convolution for image classification. In CVPR, 2017. 5

[28] Y. Jia, C. Huang, and T. Darrell. Beyond spatial pyramids: Receptive field learning for pooled image features. In CVPR, 2012. 6

[29] A. Kanazawa, A. Sharma, and D. Jacobs. Locally scale-invariant convolutional neural networks. In NIPS, 2014. 6

[30] J. J. Koenderink and A. J. van Doom. Representation of local geometry in the visual system. Biological Cybernetics, 55(6):367–375, Mar. 1987. 6

[31] A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, 2012. 1

[32] D. Laptev and J. M. Buhmann. Transformation-invariantcon-volutional jungles. In CVPR, 2015. 6

[33] D. Laptev, N. Savinov, J. M. Buhmann, and M. Pollefeys. Ti-pooling: transformation-invariant pooling for feature learning in convolutional neural networks. arXiv preprint arXiv:1604.06318, 2016. 6

[34] S. Lazebnik, C. Schmid, and J. Ponce. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. In CVPR, 2006. 6

[35] Y. LeCun and Y. Bengio. Convolutional networks for images, speech, and time series. The handbook of brain theory and neural networks, 1995. 1

[36] K. Lenc and A. Vedaldi. Understanding image representations by measuring their equivariance and equivalence. In CVPR, 2015. 6

[37] C.-H. Lin and S. Lucey. Inverse compositional spatial transformer networks. arXiv preprint arXiv:1612.03897, 2016. arXiv preprint arXiv:1409.5403, 2014. 6

[18] B. Hariharan, P. Arbeláez, L. Bourdev, S. Maji, and J. Malik. 5 Semantic contours from inverse detectors. In ICCV, 2011. 7 [19] B. Hariharan, P. Arbeláez, R. Girshick, and J. Malik. Simultaneous detection and segmentation. In ECCV. 2014. 7

[38] T.-Y. Lin, P. Dollár, R. Girshick, K. He, B. Hariharan, and S. Belongie. Feature pyramid networks for object detection. In CVPR, 2017. 4, 7

[39] T.-Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona, D. Ramanan, P. Dollár, and C. L. Zitnick. Microsoft COCO: Common objects in context. In ECCV. 2014. 7

[40] W. Liu, D. Anguelov, D. Erhan, C. Szegedy, and S. Reed. Ssd: Single shot multibox detector. In ECCV, 2016. 1, 4

[41] J. Long, E. Shelhamer, and T. Darrell. Fully convolutional networks for semantic segmentation. In CVPR, 2015. 1, 6, 7

[42] D. G. Lowe. Object recognition from local scale-invariant features. In ICCV, 1999. 1, 6

[43] W. Luo, Y. Li, R. Urtasun, and R. Zemel. Understanding the effective receptive field in deep convolutional neural networks. arXiv preprint arXiv:1701.04128, 2017. 6

[44] W. Ouyang, X. Wang, X. Zeng, S. Qiu, P. Luo, Y. Tian, H. Li, S. Yang, Z. Wang, C.-C. Loy, and X. Tang. Deepid-net: Deformable deep convolutional neural networks for object detection. In CVPR, 2015. 6

[45] P. Perona. Deformable kernels for early vision. TPAMI, 1995. 6

[46] J. Redmon, S. Divvala, R. Girshick, and A. Farhadi. You only look once: Unified, real-time object detection. In CVPR, 2016. 1

[47] S. Ren, K. He, R. Girshick, and J. Sun. Faster R-CNN: Towards real-time object detection with region proposal networks. In NIPS, 2015. 1, 3, 4, 6, 7

[48] S. Ren, K. He, R. Girshick, and J. Sun. Faster R-CNN: Towards real-time object detection with region proposal networks. TPAMI, 2016. 7

[49] E. Rublee, V. Rabaud, K. Konolige, and G. Bradski. Orb: an efficient alternative to sift or surf. In ICCV, 2011. 6

[50] K. Sohn and H. Lee. Learning invariant representations with local transformations. In ICML, 2012. 6

[51] C. Szegedy, S. Ioffe, V. Vanhoucke, and A. Alemi. Inception-v4, inception-resnet and the impact of residual connections on learning. arXiv preprint arXiv:1602.07261, 2016. 4, 10

[52] C. Szegedy, S. Reed, D. Erhan, and D. Anguelov. Scalable, high-quality object detection. arXiv:1412.1441v2, 2014. 1

[53] D. E. Worrall, S. J. Garbin, D. Turmukhambetov, and G. J. Brostow. Harmonic networks: Deep translation and rotation equivariance. arXiv preprint arXiv:1612.04642, 2016. 6

[54] F. Yu and V. Koltun. Multi-scale context aggregation by dilated convolutions. In ICLR, 2016. 6

[55] F. Yu, V. Koltun, and T. Funkhouser. Dilated residual networks. In CVPR, 2017. 6