前言
上一篇《数据结构和算法》中我介绍了数据结构的基本概念,也介绍了数据结构一般可以分为逻辑结构和物理结构。逻辑结构分为集合结构、线性结构、树形结构和图形结构。物理结构分为顺序存储结构和链式存储结构。并且也介绍了这些结构的特点。然后,又介绍了算法的概念和算法的5个基本特性,分别是输入、输出、有穷性、确定性和可行性。最后说阐述了一个好的算法需要遵守正确性、可读性、健壮性、时间效率高和存储量低。其实,实现效率和存储量就是时间复杂度和空间复杂度。本篇我们就围绕这两个"复杂度"展开说明。在真正的开发中,时间复杂度尤为重要,空间复杂度我们不做太多说明。
时间复杂度
时间复杂度和空间复杂度是算法效率的度量方法。也就是说,一个好的算法取决于它的时间复杂度和空间复杂度。
函数的渐近增长:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大。那么,我们说f(n)的增长渐近快于g(n)。
翻译过来就是:如果存在一个临界值,使得f(n)>g(n)永远成立,那么我们就认为"f(n)的增长渐近快于g(n)"。
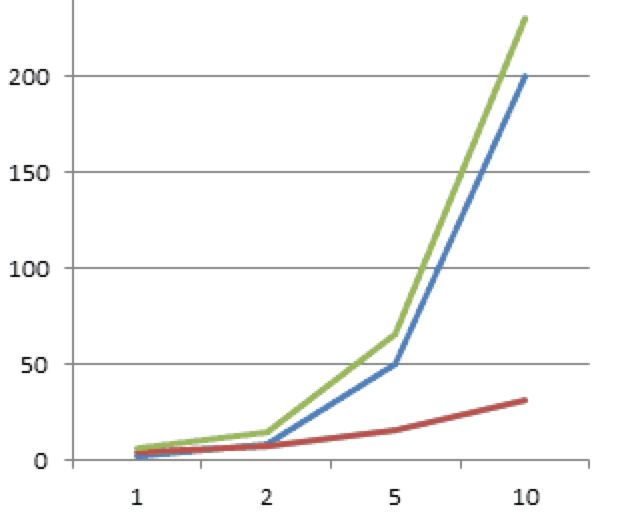
这里我拿3个函数的增长曲线来说明问题。如下图:
函数一:X = 3n 注释:3乘以n
函数二:Y = 2n^2 注释:n的平方乘以2
函数三:Z = 2n^2 + 3n 注释:n的平方乘以2 + 3乘以n
当n=1时,Y < X < Z.
当n=2时,X < Y < Z.
所以,存在一个值,这个值位于1和2之间,使得X < Y < Z永远成立。我们就称Y的渐进增长快于X,Z的渐进增长快于Y,当然,根据传递性规则,Z的渐进增长也快于X。
定义
算法时间复杂度的定义:在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。
算法的时间复杂度,也就是算法的时间量度,记作:T(n)= O(f(n))。
它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度。其中f(n)是问题规模n的某个函数。
时间复杂度计算方法
1.用常数1取代运行时间中的所有加法常数。
2.在修改后的运行次数函数中,只保留最高阶项。
3.如果最高阶项存在且不是1,则去除与这个项相乘的常数。
最后,得到的最后结果就是时间复杂度。
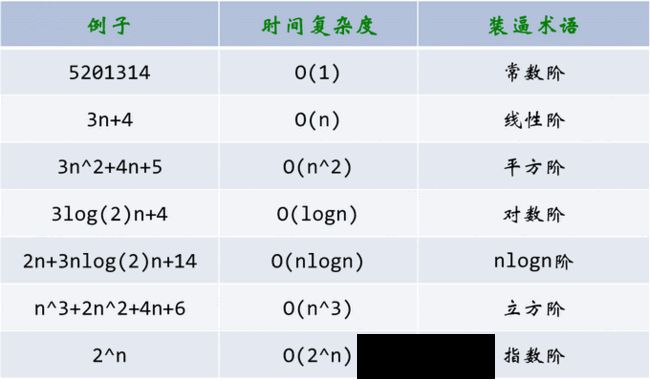
常见的时间复杂度
按数量级递增排列,常见的时间复杂度有:
常数阶O(1),对数阶O( log n ),线性阶O(n),线性对数阶O(nlog2n),平方阶O(n2),立方阶O(n3),...,k次方阶O(nk),指数阶O(2n)。随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
也就是:
常用的时间复杂度所耗费的时间从小到大依次是:O(1) < O(logn) < (n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
常数阶
// 常数阶
int n = 0;
printf(“oneSong”);
printf(“oneSong”);
printf(“oneSong”);
printf(“oneSong”);
printf(“oneSong”);
printf(“oneSong”);
printf(“oneSong”);
printf(“oneSong”);
printf(“oneSong”);
上面这段代码的时间复杂度是O(1)。因为,按照时间复杂度的定义来说,n和问题的规模没有关系。当然,按照时间复杂度计算方法第一条也可以得出结果为O(1)。
线性阶
// 线性阶int i ,
n = 10086, sum = 0;
for( i=0; i < n; i++ )
{
sum = sum + i;
}
上面这段代码的时间复杂度是O(n),因为问题规模会随着n的增长而变得越来越大,并且这种增长是线性的。
平方阶
// 平方阶
int i, j, n = 998;
for( i=0; i < n; i++ )
{
for( j=0; j < n; j++ )
{
printf(“oneSong”);
}
}
上面这段代码外层执行n次,外层循环每执行一次,内层循环就执行n次,那总共程序想要从这两个循环出来,需要执行n*n次,也就是n的平方。所以这段代码的时间复杂度为O(n^2)。
对数阶
// 对数阶
int i = 1, n = 100;
while( i < n )
{
i = i * 2;
}
由于每次i*2之后,就距离n更近一步,假设有x个2相乘后大于或等于n,则会退出循环。于是由2^x = n得到x = log(2)n,所以这个循环的时间复杂度为O(logn)。
算法的空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法的空间复杂度的计算公式记作:S(n)=O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
在程序开发中,我们所指的复杂度不做特别说明的情况下,就是指时间复杂度。现在的硬件发展速度之快使得我们完全可以不用考虑算法所占的内存,通常都是用空间换取时间。加之算法的空间复杂度比较难算,所以,无论是在考试中还是在项目开发中,我们都侧重于时间复杂度。所以,空间复杂度,略过。
图片来源参考自:鱼C工作室。感谢鱼C工作室贡献出了这么好的图片。
如非特别说明,笔者所有文章都是原创文章。如果您喜欢这篇文章,转载请注明出处。如果您对数据结构感兴趣,请关注我,后续会更新大量精品文章供大家参考!
PS:本篇文章在博客园也有同步更新,大家也可以通过博客园关注我
http://www.cnblogs.com/wsnb