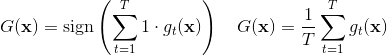第二十八节集成学习之随机森林概念介绍(1)
从本系列开始,我们讲解一个新的算法系列集成学习。集成学习其实是怎么样去应用决策树解决一些问题。
在机器学习领域集成学习是一种非常简单直接的提升分类器回归器预测效果的一种思路。决策树有一个困境,当层数太深的时候会有过拟合问题,当我不想过拟合,就通过预剪枝给它砍掉一部分深度,此时损失又容易太大了,导致在训练集上预测的又不怎么准。所以对于决策树很难去找到一个权衡的点,让它既损失小一点,又别过拟合了,很难通过预剪枝来判断到底应该剪到哪层最好,有可能剪到哪一层都不太好,于是就产生了集成学习的那种思路。
集成学习是搞出一堆树来,然后让每一棵树都做一个预测,最后大家投票,比如说搞出了一百棵树,来一条新数据,一百棵树会给你一百个结果,那么这一百个结果是一样的还是不一样的,取决于怎么训练的这一百棵数。拿一份数据去训练一百棵,一千棵,一万棵都是一模一样的,已经注定了,因为它的评价标准都是一样的。但假如你通过某种手段,认为一百棵树彼此不太相同,它们预测结果也会有的相同,有的不相同,少数服从多数,最终预测出来的结果就是集成学习学完的结果。
上面每一颗树就是一个弱分类器,所以我们总结下集成学习的思路是:
1.训练出若干的弱分类器,或者弱回归器,它们都比较弱。
2.把数据交给每一个弱分类器,得到一个结果,再把所有预测结果统一在一起。不同的机器学习的策略,会用不同的方式来运用最终的结果。
我们举个例子来说明下:
假设你有15个朋友给你出主意投资股票,怎么做最终的决定?假如说只有买或不买两个选项,那怎么决定到底买还是不买?第一个思路是假如15个人里14个都说买,一个说不买,我就听从他们意见就买了。这是一个直观的想法,所有朋友的意见投票, 少数服从多数。第二个思路是可以根据朋友靠不靠谱去判断一下,要不要多考虑一下他的意见,比如有一个人投资回报率是80%,有一个人投资回报率是-200%,现在两个人一个说买,一个说不买,那么就着重的听投资回报率高的朋友。所以这就是选择最牛x的一个朋友的意见当做自己的意见。第三个思路假如做的好的投一票顶五票,做得比较差的投一票就顶一票。最后四个挺弱的人都说买,一个大师说不买,你也会听大师的,因为它手里的票数比较多。那么就会给他们分配不同的票数,比较厉害的人票数多一点,比较差的票数少一点,最后做一个带着票数的不均匀的投票。这就是投票 牛x一点的朋友多给几票, 弱鸡一点的少给几票。假设现在有一个一辈子买什么都跌的人,从来没买中过一次,跟你说买,另外一个投资回报率100%的人也说买,那到底结果是买还是不买,落实到机制上来说,就是一些分类器,你给它负的票,也可以给你提供一个信息量。最后我们再综合考虑。
对于15个朋友投票的问题来说,能有显而易见的两种策略,一种叫均匀投票,一种叫做带权重的投票。 所谓带权重的投票是,你厉害我就更重视一点,你表达的意见对最终结果的影响更大一点。而均匀投票代表所有人的意见我认为你们都是一视同仁的。
这两种策略如何决定?什么时候使用?取决于这15个朋友是什么样的,如果15个朋友水平差不多,投票更合理,因为从主观意愿去给一些人更大的权重,最后模型的效果一般不会好。假如15个朋友参差不齐,那么我们可能对那些靠谱或者牛X一点的朋友的意见考虑的更大些,实际上就是对他们的每个人的投票结果给予不同的权重。这种均匀投票的方式就是随机森林,而带权重投票的方式叫Adaboost。这是两种不同的集成学习的方式。
我们用数学形式来表达下上面两种不同的思路,Aggregation是聚合的意思,我们集成学习是把若干的弱分类器的预测结果聚合到一起,汇总成一个结果。
第一种:所有朋友的意见投票, 少数服从多数
解释下:这里的gt(x)就是一棵决策树,给它写成一个函数gt(x),当成黑盒,代表给我一个x,告诉你一个结果。二分类就是给我一个函数,告诉你是+1还是-1。多分类就是给我一个函数,告诉你是1,2,还是3。给它写成gt(x)就代表它是决策树的预测结果。t代表它的序号,是从1到T,代表我们有T个弱分类器,其中每一个gt(x)代表某一个弱分类器的结果,假设正例是+1,负例是-1的情况下,把它们统统加起来,假如最后结果是正的,就代表投票的+1比较多;最后的结果是负的,代表-1比较多。sign是一个简单的取符号的运算,当这个里边的计算结果为正的时候,比如+100,前面加上sign,结果就等于+1;假如运算结果是-10000,前面加上sign,结果等于-1。也就是G(x)最后的结果,要么是+1,要么是-1。假如是多分类问题,就很难通过解析式来表达了,它无非还是一个投票,有一百个弱分类器,50个是1,20个是2,30个是3,最后的投票结果就是1。这是对于分类问题,如果是回归问题,每一个弱分类器会给出一个结果,假设第一个弱分类器是100,第二120,第三200,第四500,那么最终把它们取个平均数,就作为最终的预测结果。我们称这种聚合方式叫做均匀混合(uiform blending ),Blend是搅拌混合的意思,就是说训练好了若干个弱分类器之后,一条数据分别交给它们预测,把它们的预测结果杂糅在一起,最后汇总出的结果,这个过程就叫做Blending。
第二种:还是投票 牛x一点的朋友多给几票, 弱鸡一点的少给几票
解释下:这里面的αt代表每一个弱分类器给它一个单独的权重,如果弱分类器表现好,我就给你的αt大点,如果表现的不好,我就给你的αt小点,如果还是投票,厉害的人票多,代表α要大一点;对于买什么什么赔的,他的α一定是负数,这个式子表达的就是赋予每个人不同票数的这种投票方式。如果训练出来的弱分类器正确率低于50%的情况下,会有两种处理方式,第一种就是给它投一个负票,但它有可能是由极端的偶然导致的,因为它训练出来的结果太差了,不代表什么意义,所以第二种处理方式会把它丢弃,这也正是为什么αt>=0的原因。
对于均匀混合(uiform blending )方式,已知所有的gt(x),把它的均匀的聚合到一起,就得到了一个最终的结果,但假如所有的gt(x)都是相同的,就独裁了,相当于一千个投票一千个人意见都是一样的,投票没有任何意义了。所以只有一些不同的朋友们给你带来各种各样的意见的情况下,投票才能带来一些提升。所以这就意味着我们在生成gt(x)的时候应该考虑制造一些每个人看法迥异,但多少都有些道理的gt(x)。
那具体怎么生成gt(x)呢?我们这里引入两个概念:分别为Bagging和Boosting。
Bagging通过一个叫bootstrap的抽样,进行有放回的对原始数据集进行均匀抽样。假如现在有一百条数据,用有放回地进行抽样话,原来有100条数据,现在还有100条数据,抽到的数据有可能会跟原来一模一样的。当这个值不是100,而是足够大的一个值的时候,我们要抽一些数据作为每一个弱分类器的训练样本,一些数据肯定会被多次抽中,也有一些数据永远不会被抽中。在集成学习里面,我们并不强调每个gt(x)是什么,因为它就对应一个弱分类器,这里gt(x)可以是任何一个算法,svm ,逻辑回归等等,类似于分类器的一个黑盒子。当这里gt(x)是决策树的时候,我们称这种集成方式为随机森林。假如随机森林需要一百棵树投票,那么就制造100份训练集,每一个训练集怎么生成的,就是通过有放回的随机抽样生成100个与众不同的训练集。这种抽样方法对每个人都是公平的,最后用一百个树公平的投票。因为我们是均匀的随机抽样,所以虽然这些树里面有好有坏,但是我对它们一视同仁,因为我也不知道哪一棵树好,哪一棵树坏,按理说,只要坏数据少,生成的坏树应该比好树少,那最后投票的时候,会把坏树的意见屏蔽掉,这样操作之后,训练集的准确性会提高。另一方面我们看下随机森林的原始论文定义:
从这里面可以看出随机森林就是Bagging和decision-tree的结合,decision-tree就是决策树,fully-grown就是不经过任何剪枝,就让它完全的自由生长的这种树,再通过Bagging这种方式结合,得到这个算法就叫做Random Forest。对于Random Forest,它需要一个原始的训练集D,通过bootstrapping得到这个东西叫Dt树,要得到多少个Dt树,取决于需要多少棵树,每一个Dt训练出一棵树,最终你有多少个Dt,就有多少个树,最后得到从Dt上训练出来的gt(x),最后G的结果是把gt(x)均匀混合起来。所以随机森林的优点:
第一:它可以并行训练,它是一个非常适合并行训练的模式,只要把所有的训练集准备好,接下来的训练它们彼此之间没有关系了,只要需要自己的Dt就可以了。
第二:对于CART树里面的所有的优势,它全都继承下来了,它可以解决非线性问题,它可以做分类也可以做回归。
第三:它可以把fully-grown过拟合的性质,通过均匀投票,来减轻过拟合的这种情况。不可能所有的树全都过拟合了,因为随机得到的训练集是不一样的。对同一套数据,有少部分过拟合没关系,因为最终还要投票,那些过拟合的树它的投票结果,只要占少数就被干掉了,最终不会考虑它的意见,所以它对于过拟合的这种情况也是有一个很好的对抗。
即便随机森林它倾向于完全长成的树,但在实践中全训练,不加预剪枝的树速度太慢,所以通常也会预剪枝,只不过把它层数限制的深一些,20层,30层,它就近似的有这种完全长成树的这种特性。否则你真的让它分到每一个节点,分到最纯才停的话太慢了。
那随机森林里的随机都有哪些随机呢?第一个随机是有放回的随机抽样;第二个随机是它对于特征还会随机取,在训练单棵决策树的时候,随意一个特征在训练的过程中算法都能看到,而随机森林它刻意的不让你看到所有特征,它随机选几个特征,让小树看,比如有x1到x100,随机选出十个特征来,这个分类器就更弱一点,而且更加的与众不同。因为谁跟谁看到的事都不一样,而且差异还挺大,因为行上的样本不一样,列上能看到的维度又不一样。虽然不一样,但它们都很公平,都是让随机抽的,最终也能用公平的方式均匀地把它做一个投票。所以第二点就是通过随机保留部分特征,来进一步的增加每一个弱分类器之间的差异性,最终训练出若干个弱分别器,就可以投票得到结果。第三点这个东西虽然没有实现,在树模型中,如果随机的将feature进行一些线性组合,作为新的feature,是对它有帮助的。
下一节中我们会对随机森林中的第三种随机方式展开讲,也会讲解一个新的东西,out of bag data以及随机森林的一些封装的API。