198. House Robber【Easy DP】
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
时间O(N) 空间O(n)
这道题的实质就是找一个整数集里面的取出一个或多个不相邻数,使其和最大。
首先会考虑Dynamic Programming的写法。
Base Case: 第一家的钱 或者 第二家的钱 (the money in the first house or second house)
Induction Rule: M[i] 表示到i位置时不相邻数能形成的最大和。 represents the max sum till the ith position. M[i] = Math.max(money[i] + M[i - 2], M[i - 1]);
public class Solution {
public int rob(int[] nums) {
int[] M = new int[nums.length];
if(nums.length <= 1) {
return nums.length == 0? 0: nums[0];
}
M[0] = nums[0];
M[1] = Math.max(nums[0], nums[1]);
for(int i = 2; i < nums.length; i++) {
M[i] = Math.max( (nums[i] + M[i-2]), M[i-1]) ;
}
return M[nums.length - 1];
}
}
可以进一步优化为O(1)的空间复杂度
public class Solution {
public int rob(int[] nums) {
if(nums.length <= 1) {
return nums.length == 0? 0: nums[0];
}
int preMax = nums[0];
int curMax = Math.max(nums[0], nums[1]);
for(int i = 2; i < nums.length; i++) {
int tem = b;
b = Math.max( (nums[i] + a), b) ;
}
return b;
}
}
213. House Robber II
Note: This is an extension of House Robber.
After robbing those houses on that street, the thief has found himself a new place for his thievery so that he will not get too much attention. This time, all houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, the security system for these houses remain the same as for those in the previous street.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
**在上一题的基础上,加了个条件,就是如果偷了第一家的钱,那么一定不能偷最后一家。分别算出抢第一家和不抢第一家这两种情况下的收益,选最大
base case: 偷第一家, 或者偷第二家
Induction rule:M[i] 表示到i位置时不相邻数能形成的最大和。 represents the max sum till the ith position. M[i] = Math.max(money[i] + M[i - 2], M[i - 1]);
最后的结果返回Math.max(M[1 - (n - 1)] , M[0 - (n-2)]); **
时间O(n) 空间O(1)
public class Solution {
public int rob(int[] nums) {
return Math.max(rob(nums, 0), rob(nums, 1) );
}
public int rob(int[] nums, int offset){
if(nums.length <= 1+offset){
return nums.length <= offset ? 0 : nums[0 + offset];
}
int preMax = nums[0 + offset];
int curMax = Math.max( nums[1 + offset], nums[0 + offset]);
for(int i = 2 + offset; i < nums.length - 1 + offset; i++){
int temp = curMax;
curMax = Math.max(preMax + nums[i], curMax);
preMax = temp;
}
return curMax;
}
}
337. House Robber III
The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the "root." Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that "all houses in this place forms a binary tree". It will automatically contact the police if two directly-linked houses were broken into on the same night.
Determine the maximum amount of money the thief can rob tonight without alerting the police.
Example 1:
3
/ \
2 3
\
3 1
Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
Example 2:
3
/
4 5
/ \ \
1 3 1
Maximum amount of money the thief can rob = 4 + 5 = 9.
Native Solution:
Step I -- Think naively
At first glance, the problem exhibits the feature of "optimal substructure": if we want to rob maximum amount of money from current binary tree (rooted at root), we surely hope that we can do the same to its left and right subtrees.So going along this line, let's define the function rob(root) which will return the maximum amount of money that we can rob for the binary tree rooted at root; the key now is to construct the solution to the original problem from solutions to its subproblems, i.e., how to get rob(root) from rob(root.left),rob(root.right), ...
etc.
Apparently the analyses above suggest a recursive solution. And for recursion, it's always worthwhile figuring out the following two properties:
Termination condition: when do we know the answer to rob(root)
without any calculation? Of course when the tree is empty -- we've got nothing to rob so the amount of money is zero.
Recurrence rule: i.e., how to get rob(root)
from rob(root.left), rob(root.right), ...
etc. From the point of view of the tree root, there are only two scenarios at the end: root
is robbed or is not. If it is, due to the constraint that "we cannot rob any two directly-linked houses", the next level of subtrees that are available would be the four "grandchild-subtrees" (root.left.left, root.left.right, root.right.left, root.right.right). However if root
is not robbed, the next level of available subtrees would just be the two "child-subtrees" (root.left, root.right). We only need to choose the scenario which yields the larger amount of money.
Here is the program for the ideas above:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public int rob(TreeNode root) {
if(root == null) {
return 0;
}
int max = 0;
if(root.left != null) {
max += rob(root.left.left) + rob(root.left.right);
}
if(root.right != null) {
max += rob(root.right.left) + rob(root.right.right);
}
return Math.max(rob(root.left) + rob(root.right), root.val + max);
}
}
Step II -- Think one step further
In step I
, we only considered the aspect of "optimal substructure", but think little about the possibilities of overlapping of the subproblems. For example, to obtain rob(root), we need rob(root.left), rob(root.right), rob(root.left.left), rob(root.left.right), rob(root.right.left), rob(root.right.right); but to get rob(root.left), we also needrob(root.left.left), rob(root.left.right), similarly for rob(root.right). The naive solution above computed these subproblems repeatedly, which resulted in bad time performance. Now if you recall the two conditions for dynamic programming: "optimal substructure" + "overlapping of subproblems", we actually have a DP problem. A naive way to implement DP here is to use a hash map to record the results for visited subtrees.
And here is the improved solution:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public int rob(TreeNode root) {
return helper(root, new HashMap<>());
}
private int helper(TreeNode root, HashMap myMap){
if(root == null) {
return 0;
}
if(myMap.containsKey(root)){
return myMap.get(root);
}
int max = 0;
if(root.left != null) {
max += helper(root.left.left, myMap) + helper(root.left.right, myMap);
}
if(root.right != null) {
max += helper(root.right.left, myMap) + helper(root.right.right, myMap);
}
max = Math.max(helper(root.left, myMap) + helper(root.right, myMap), root.val + max);
myMap.put(root, max);
return max;
}
}
The runtime is sharply reduced to 9 ms, at the expense of O(n)
space cost (n is the total number of nodes; stack cost for recursion is not counted).
Step III -- Think one step backIn step I, we defined our problem as rob(root), which will yield the maximum amount of money that can be robbed of the binary tree rooted at root. This leads to the DP problem summarized in step II.
Now let's take one step back and ask why we have overlapping subproblems. If you trace all the way back to the beginning, you'll find the answer lies in the way how we have defined rob(root). As I mentioned, for each tree root, there are two scenarios: it is robbed or is not.rob(root) does not distinguish between these two cases, so "information is lost as the recursion goes deeper and deeper", which results in repeated subproblems.
If we were able to maintain the information about the two scenarios for each tree root,let's see how it plays out. Redefine rob(root) as a new function which will return an array of two elements, the first element of which denotes the maximum amount of money that can be robbed if root is not robbed, while the second element signifies the maximum amount of money robbed if it is robbed.Let's relate rob(root) to rob(root.left) and rob(root.right)..., etc. For the 1st element of rob(root), we only need to sum up the larger elements of rob(root.left) and rob(root.right), respectively, since root is not robbed and we are free to rob its left and right subtrees. For the 2nd element of rob(root), however, we only need to add up the 1st elements of rob(root.left) androb(root.right), respectively, plus the value robbed from root itself, since in this case it's guaranteed that we cannot rob the nodes ofroot.left and root.right.
As you can see, by keeping track of the information of both scenarios, we decoupled the subproblems and the solution essentially boiled down to a greedy one. Here is the program:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public int rob(TreeNode root) {
int[] res = helper(root);
return Math.max(res[0], res[1]);
}
private int[] helper(TreeNode root) {
if (root == null) return new int[2];
int[] left = helper(root.left);
int[] right = helper(root.right);
int[] res = new int[2];
res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
res[1] = root.val + left[0] + right[0];
return res;
}
}
55. Jump Game
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Determine if you are able to reach the last index.
For example:
A = [2,3,1,1,4], return true.
A = [3,2,1,0,4], return false.
使用一维DP linear scan 回头看的思想
base case: 数组里面最后一个空位跳到本身需要的jump length
Induction Rule:M[i] 代表了 每次从 i 这个位置能否跳到最后或者是否能跳到一个为True的元素位置(跳到一个自身鞥跳到最后的位置)
if nums[i] >= n - i || nums[j] = true (j = i 到n之间) M[i] = true
public boolean canJump(int[] array) {
boolean[] canJumap = new boolean[array.length];
canJump[0] = true;
for(int i = 1; i < array.length; i++) {
for(int j = 0; j < i; j++) {
if(canJump[j] && array[j] + j >= i) {
canJump[i] = true;
break;
}
}
}
return canJump(array.length - 1);
}
53. Maximum Subarray
Find the contiguous subarray within an array (containing at least one number) which has the largest sum.
For example, given the array [-2,1,-3,4,-1,2,1,-5,4],
the contiguous subarray [4,-1,2,1] has the largest sum = 6.
// 用dp解题
//保存一个
//induction rule : if sum > 0 -> sum += array[i] else -> sum = array[i]
//base case is the first one integer: M[0] = array[0]
[-2,1,-3,4,-1,2,1,-5,4]
-2 1 -3 4 3 5 6 6 6
public int maxSubArray(int[] nums) {
if(nums == null) {
return 0;
}
int max = nums[0];
int result = nums[0];
for(int i = 1; i < nums.length; i++) {
if(max >= 0){
max += nums[i];
}else{
max = nums[i];
}
result = Math.max(max, result);
}
return result;
}
- Range Sum Query - Immutable
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
Example:
Given nums = [-2, 0, 3, -5, 2, -1]sumRange(0, 2) -> 1sumRange(2, 5) -> -1sumRange(0, 5) -> -3
Note:
You may assume that the array does not change.
There are many calls to sumRange function.
//Can use DP or DFS
DP解法:
用一个一维数组存入到每个整数的prefix sum
public class NumArray {
int[] M;
public NumArray(int[] nums) {
for(int i = 1; i < nums.length; i++) {
nums[i] = nums[i - 1] + nums[i];
}
this.M = nums;
}
public int sumRange(int i, int j) {
if(i == 0) {
return M[j];
}
return M[j] - M[i - 1];
}
}
276.Paint Fence
There is a fence with n posts, each post can be painted with one of the k colors.
You have to paint all the posts such that no more than two adjacent fence posts have the same color.
Return the total number of ways you can paint the fence.
Note: n and k are non-negative integers.
base case : the first wall
1 2
public class Solution {
public int numWays(int n, int k) {
if (n == 0 || k == 0)
return 0;
if (n == 1)
return k;
int same_count = k;
int differ_count = k * (k - 1);
for (int i = 3; i <= n; i++) {
int temp = differ_count;
differ_count = differ_count * (k - 1) + same_count * (k - 1);
same_count = temp;
}
return same_count + differ_count;
}
}
121. Best Time to Buy and Sell Stock
Say you have an array for which the ith element is the price of a given stock on day i. If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Example 1:
Input: [7, 1, 5, 3, 6, 4]Output: 5max. difference = 6-1 = 5 (not 7-1 = 6, as selling price needs to be larger than buying price)
Example 2:
Input: [7, 6, 4, 3, 1]Output: 0In this case, no transaction is done, i.e. max profit = 0.
//此题很简单,只需要遍历一次数组,用一个变量记录遍历过数中的最小值,然后每次计算当前值和这个最小值之间的差值最为利润,然后每次选较大的利润来更新。当遍历完成后当前利润即为所求,代码如下:
public class Solution {
public int maxProfit(int[] prices) {
if(prices == null || prices.length <= 1){
return 0;
}
int max = 0;
int min = prices[0];
for(int i = 1; i < prices.length; i++) {
min = Math.min(min, prices[i]);
max = Math.max(prices[i] - min, max);
}
return max;
}
}
309. Best Time to Buy and Sell Stock with Cooldown
Say you have an array for which the ith element is the price of a given stock on day i.Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:
prices = [1, 2, 3, 0, 2]maxProfit = 3transactions = [buy, sell, cooldown, buy, sell]
The natural states for this problem is the 3 possible transactions : buy, sell, rest. Here rest means no transaction on that day (aka cooldown). Then the transaction sequences can end with any of these three states. For each of them we make an array, buy[n], sell[n] and rest[n].
buy[i] means before day i
what is the maxProfit for any sequence end with buy.
sell[i] means before day i what is the maxProfit for any sequence end with sell.
rest[i] means before day i what is the maxProfit for any sequence end with rest.
Then we want to deduce the transition functions for buy sell and rest. By definition we have:
buy[i] = max(rest[i-1]-price, buy[i-1]) sell[i] = max(buy[i-1]+price, sell[i-1])rest[i] = max(sell[i-1], buy[i-1], rest[i-1])
Where price
is the price of day i
. All of these are very straightforward. They simply represents :
(1) We have to rest before we buy and (2) we have to buy before we sell
One tricky point is how do you make sure you sell before you buy, since from the equations it seems that [buy, rest, buy] is entirely possible. Well, the answer lies within the fact that buy[i] <= rest[i] which means rest[i] = max(sell[i-1], rest[i-1]). That made sure [buy, rest, buy] is never occurred. A further observation is that and rest[i] <= sell[i] is also true therefore rest[i] = sell[i-1] Substitute this in to buy[i] we now have 2 functions instead of 3:
_
buy[i] = max(sell[i-2]-price, buy[i-1])
sell[i] = max(buy[i-1]+price, sell[i-1])
_
This is better than 3, but
we can do even better
Since states of day i relies only on i-1and i-2we can reduce the O(n) space to O(1). And here we are at our final solution:
public class Solution {
public int maxProfit(int[] prices) {
int sell = 0, prev_sell = 0, buy = Integer.MIN_VALUE, prev_buy;
for (int price : prices) {
prev_buy = buy;
buy = Math.max(prev_sell - price, prev_buy);
prev_sell = sell;
sell = Math.max(prev_buy + price, prev_sell);
}
return sell;
}
}
122. Best Time to Buy and Sell Stock II
Say you have an array for which the ith element is the price of a given stock on day i.Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times). However, you may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
这题只需要loop整个prices数组,只需要从第二天开始,如果当前价格比之前价格高,则把差值加入利润中,因为我们可以昨天买入,今日卖出,若明日价更高的话,还可以今日买入,明日再抛出。以此类推,遍历完整个数组后即可求得最大利润。代码如下:
public class Solution {
public int maxProfit(int[] prices) {
if(prices == null || prices.length == 0){
return 0;
}
int profit = 0;
for(int i = 1; i < prices.length; i++) {
if(prices[i] > prices[i - 1]) {
profit += prices[i] - prices[i-1];
}
}
return profit;
}
}
- Best Time to Buy and Sell Stock III
Say you have an array for which the ith element is the price of a given stock on day i. Design an algorithm to find the maximum profit. You may complete at most two transactions.
Note:You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
//可以以每个price为分界点,把price分为两个部分,把第一部分的最大profit加上第二部分的profit放到M, 返回最大的profit和
//M[i]代表了以i为分界点的左右两边最大profit的和
//M[0]等于整个int array 的最大profit
public int maxProfit(int[] prices) {
if (prices.length == 0){
return 0;
}
int[] profitUntil = new int[prices.length];
int[] profitFrom = new int[prices.length];
//Calculate the profit until i.
int minValue = prices[0];
profitUntil[0] = 0;
for (int i = 1; i < prices.length; i++) {
minValue = Math.min(minValue, prices[i]);
profitUntil[i] = Math.max(profitUntil[i - 1], prices[i] - minValue);
}
//Calculate the profit from i.
profitFrom[prices.length - 1] = 0;
int maxValue = prices[prices.length - 1];
for (int i = prices.length - 2; i >= 0; i--) {
maxValue = Math.max(maxValue, prices[i]);
profitFrom[i] = Math.max(profitFrom[i + 1], maxValue - prices[i]);
}
int maxProfit = 0;
for (int i = 0; i < prices.length; i++){
maxProfit = Math.max(maxProfit, profitUntil[i] + profitFrom[i]);
}
return maxProfit;
}
}
375. Guess Number Higher or Lower II
We are playing the Guess Game. The game is as follows:
I pick a number from 1 to n. You have to guess which number I picked.
Every time you guess wrong, I'll tell you whether the number I picked is higher or lower.
However, when you guess a particular number x, and you guess wrong, you pay $x. You win the game when you guess the number I picked.
Example:
n = 10, I pick 8.First round: You guess 5, I tell you that it's higher. You pay $5.Second round: You guess 7, I tell you that it's higher. You pay $7.Third round: You guess 9, I tell you that it's lower. You pay $9.Game over. 8 is the number I picked.You end up paying $5 + $7 + $9 = $21.
Given a particular n ≥ 1, find out how much money you need to have to guarantee a win.
public class Solution {
public int getMoneyAmount(int n) {
int[][] M = new int[n + 1][n + 1];
return DP(M, 0, n);
}
private int DP(int[][] M, int start, int end) {
if(start >= end) {
return 0;
}
if(M[start][end] != 0) {
return M[start][end];
}
int res = Integer.MAX_VALUE;
for(int i = start; i <= end; i++) {
int temp = i + Math.max(DP(M, start, i - 1), DP(M, i+1, end));
res = Math.min(res,temp);
}
M[start][end] = res;
return res;
}
}
264. Ugly Number II
Write a program to find the n-th ugly number.Ugly numbers are positive numbers whose prime factors only include 2, 3, 5. For example, 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 is the sequence of the first 10 ugly numbers.
Note that 1 is typically treated as an ugly number.
Hint:
The naive approach is to call isUgly for every number until you reach the nth one. Most numbers are not ugly. Try to focus your effort on generating only the ugly ones. An ugly number must be multiplied by either 2, 3, or 5 from a smaller ugly number.
The key is how to maintain the order of the ugly numbers. Try a similar approach of merging from three sorted lists: L1, L2, and L3.
Assume you have Uk, the kth ugly number. Then Uk+1 must be Min(L1 * 2, L2 * 3, L3 * 5).
public int nthUglyNumber(int n) {
//ungly number base case: 2 3 5
int[] M = new int[n];
M[0] = 1;
int indexTwo = 0, indexThree = 0, indexFive = 0;
int factorTwo = 2, factorThree = 3, factorFive = 5;
for(int i = 1; i < n; i++) {
int min = Math.min(Math.min( factorTwo, factorThree) , factorFive);
M[i] = min;
if(factorTwo == min) {
factorTwo = 2 * M[++indexTwo];
}
if(factorThree == min) {
factorThree = 3 * M[++indexThree];
}
if(factorFive == min) {
factorFive = 5 * M[++indexFive];
}
}
return M[n - 1];
}
64. Minimum Path Sum
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
这道题跟 Dungeon Game 很像,用动态规划Dynamic Programming来做,维护一个二维数组,其中M[i][j]表示当前位置的最小路径和,递推式 M[i][j] = M[i][j] + min(M[i - 1][j], 代码如下:
public class Solution {
public int minPathSum(int[][] grid) {
//M[i][j] represents the minimum sum from this point to the bottom right
int m = grid.length;
int n = grid[0].length;
int[][] M = new int[m][n];
M[0][0] = grid[0][0];
for(int i = 1; i < n; i++){
M[0][i] = M[0][i - 1] + grid[0][i];
}
for(int i = 1; i < m; i++){
M[i][0] += M[i - 1][0] + grid[i][0];
}
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
M[i][j] = Math.min(M[i-1][j] , M[i][j - 1]) + grid[i][j];
}
}
return M[m - 1][n - 1];
}
}
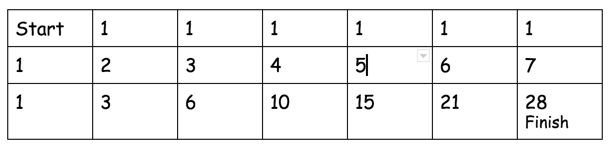
62. Unique Paths
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
**base case: 当i= 0, M[i][j] = 1 当 j = 0, M[i][j] = 1;
M[i][j] = M[i - 1][j] + M[i][j -1]
**
public class Solution {
public int uniquePaths(int m, int n) {
int[][] M = new int[m][n];
M[0][0] = 1;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(i == 0 || j == 0){
M[i][j] = 1;
}else{
M[i][j] = M[i - 1][j] + M[i][j - 1];
}
}
}
return M[m - 1][n - 1];
}
}
63. Unique Paths II
Follow up for "Unique Paths":
Now consider if some obstacles are added to the grids. How many unique paths would there be?An obstacle and empty space is marked as 1 and 0 respectively in the grid.
For example,
There is one obstacle in the middle of a 3x3 grid as illustrated below.
[
[0,0,0],
[0,1,0],
[0,0,0]
]
The total number of unique paths is 2.
Note: m and n will be at most 100.
在路径中加了一些障碍物,用动态规划Dynamic Programming来解,不同的是当遇到为1的点,将该位置的dp数组中的值清零,其余和unique path I差不多,代码如下:
public class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if (obstacleGrid == null || obstacleGrid.length == 0 || obstacleGrid[0].length == 0) {
return 0;
}
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] M = new int[m][n];
for(int i = 0; i < m; i++){
if(obstacleGrid[i][0] != 1){
M[i][0] = 1;
}else{
break;
}
}
for(int j = 0; j < n; j++){
if(obstacleGrid[0][j] != 1){
M[0][j] = 1;
}else{
break;
}
}
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
if(obstacleGrid[i][j] == 1){
M[i][j] = 0;
}else{
M[i][j] = M[i -1][j] + M[i][j - 1];
}
}
}
return M[m - 1][n - 1];
}
}
464. Can I Win !!!!
In the "100 game," two players take turns adding, to a running total, any integer from 1..10. The player who first causes the running total to reach or exceed 100 wins.
What if we change the game so that players cannot re-use integers?
For example, two players might take turns drawing from a common pool of numbers of 1..15 without replacement until they reach a total >= 100.
Given an integer maxChoosableInteger and another integer desiredTotal, determine if the first player to move can force a win, assuming both players play optimally.
You can always assume that maxChoosableInteger will not be larger than 20 and desiredTotal will not be larger than 300.
Example
Input:
maxChoosableInteger = 10
desiredTotal = 11
Output:
false
Explanation:
No matter which integer the first player choose, the first player will lose.The first player can choose an integer from 1 up to 10.If the first player choose 1, the second player can only choose integers from 2 up to 10.The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.Same with other integers chosen by the first player, the second player will always win.
记忆化搜索 + 位运算
由于maxChoosableInteger不大于20,因此可以通过整数state表示当前已经选择了哪些数字, state的第i位为1时,表示选择了数字i + 1,利用字典dp记录已经搜索过的状态
public class Solution {
private Boolean[] win;
int choosen = 0;
public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
if (desiredTotal == 0) {
return true;
}
if ((1 + maxChoosableInteger) * maxChoosableInteger / 2 < desiredTotal) {
return false;
}
win = new Boolean[1 << maxChoosableInteger];
return canWin(maxChoosableInteger, desiredTotal, 0);
}
private boolean canWin(int n, int total, int now) {
if (win[choosen] != null)
return win[choosen];
if (now >= total) {
win[choosen] = false;
return false;
}
for (int i = 1; i <= n; i++) {
int bit = 1 << (i - 1);
if ((choosen & bit) == 0) {
choosen ^= bit;
boolean ulose = !canWin(n, total, now + i);
choosen ^= bit;
if (ulose) {
win[choosen] = true;
return true;
}
}
}
win[choosen] = false;
return false;
}
}
322. Coin Change
You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
Example 1:coins = [1, 2, 5], amount = 11 return 3 (11 = 5 + 5 + 1)
Example 2:coins = [2], amount = 3 return -1.
Note:You may assume that you have an infinite number of each kind of coin.
维护一个一维动态数组M,其中M[i]表示钱数为i时的最小硬币数的找零,递推式为:
M[i] = min(M[i], M[i - coins[j]] + 1);
其中coins[j]为第j个硬币,而i - coins[j]为钱数i减去其中一个硬币的值,剩余的钱数在M数组中找到值,然后加1和当前M数组中的值做比较,取较小的那个更新dp数组
public class Solution {
public int coinChange(int[] coins, int amount) {
if(amount<1) return 0;
int[] M = new int[amount+1];
int sum = 0;
while(++sum<=amount) {
int min = -1;
for(int coin : coins) {
if(sum >= coin && M[sum-coin]!=-1) {
int temp = M[sum-coin]+1;
min = min<0 ? temp : (temp < min ? temp : min);
}
}
M[sum] = min;
}
return M[amount];
}
}
338. Counting Bits
Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1's in their binary representation and return them as an array.
Example:
For num = 5 you should return [0,1,1,2,1,2].
Follow up:
It is very easy to come up with a solution with run time O(nsizeof(integer))*. But can you do it in linear time O(n) /possibly in a single pass?
Space complexity should be O(n).
Can you do it like a boss? Do it without using any builtin function like __builtin_popcount in c++ or in any other language.
当一个数为2的整数幂的时候,1的个数为1,比如2(10) 和4(100),8(1000)
在这之后就是前一个序列的数+1 比如 9(1001) = 1(1) + 8 (1) = 2
就是把一个数分解为小于它的最大2的整数幂 + x
public class Solution {
public int[] countBits(int num) {
int[] res = new int[num+1];
int pow2 = 1,before =1;
for(int i=1;i<=num;i++){
if (i == pow2){
before = res[i] = 1;
pow2 <<= 1;
}
else{
res[i] = res[before] + 1;
before += 1;
}
}
return res;
}
}
方法2
解题思路:
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
10 1010
11 1011
12 1100
13 1101
14 1110
15 1111
........
观察上面的情况,我们发现0,1,2-3,4-7,8-15为一组,且每组开头的1的位数都是1。每组其余的数都可以用本组开头的数加上另一个差值。且这两个数都已经在前面算过了。
public int[] countBits(int num) {
//当i为2的倍数时,只有一个1. 当不为2的倍数时,等于result[i-1] + 1;
if (num < 0) {
return new int[0];
}
int[] result = new int[num + 1];
for (int i = 1; i <= num; i++) {
if ((i & 1) == 0) {
result[i] = result[i / 2];
} else {
result[i] = result[i - 1] + 1;
}
}
return result;
}
95. Unique Binary Search Trees II **
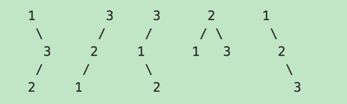
Given an integer n, generate all structurally unique BST's (binary search trees) that store values 1...n.
For example,Given n = 3, your program should return all 5 unique BST's shown below.
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public List generateTrees(int n) {
//取任意一个数为root
if(n == 0){
return new ArrayList();
}
return generate(1, n);
}
private List generate(int s, int e) {
List result = new ArrayList<>();
if(s > e) {
result.add(null);
return result;
}
for(int i = s; i <= e; i++) {
List leftNode = generate(s, i - 1);
List rightNode = generate(i + 1, e);
for(TreeNode l : leftNode){
for(TreeNode r : rightNode){
TreeNode root = new TreeNode(i);
root.left = l;
root.right = r;
result.add(root);
}
}
}
return result;
}
}
96. Unique Binary Search Trees
Given n, how many structurally unique BST's (binary search trees) that store values 1...n?
For example,Given n = 3, there are a total of 5 unique BST's.
首先注意这里是BST而不是普通的Binary Tree,所以数字会对插入的位置有影响。这类找combination/permutation的题都需要找找规律。
n = 0
n = 1
1
n = 2
1 2
\ /
2 1
n = 3
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
定义f(n)为unique BST的数量,以n = 3为例:
构造的BST的根节点可以取{1, 2, 3}中的任一数字。
如以1为节点,则left subtree只能有0个节点,而right subtree有2, 3两个节点。所以left/right subtree一共的combination数量为:f(0) * f(2) = 2
以2为节点,则left subtree只能为1,right subtree只能为2:f(1) * f(1) = 1
以3为节点,则left subtree有1, 2两个节点,right subtree有0个节点:f(2)*f(0) = 2
总结规律:
f(0) = 1
f(n) = f(0)f(n-1) + f(1)f(n-2) + ... + f(n-2)f(1) + f(n-1)f(0)**
public class Solution {
//f(n) = f(0)*f(n -1) + f(1)*f(n - 2) + ... + f(n - 1)f(0)
public int numTrees(int n) {
int[] M = new int[n + 1];
//M[i] represent the number of BST when there are i nodes
//M[0] represent the number of BST when there are 0 node, which is 1 BST can be build when there is only one node
M[0] = 1;
//1 BST can be build when there is only one node
M[1] = 1;
for(int i = 2; i <= n; i++) {
for(int j = 0; j < i; j++){
M[i] += M[j] * M[i - j - 1];
}
}
return M[n];
}
}
91. Decode Ways
A message containing letters from A-Z is being encoded to numbers using the following mapping:
Given an encoded message containing digits, determine the total number of ways to decode it.
For example,Given encoded message "12", it could be decoded as "AB"
(1 2) or "L" (12).
The number of ways decoding "12" is 2.
343. Integer Break
Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.
For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).
Note: You may assume that n is not less than 2 and not larger than 58.
120. Triangle
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
LC:
**300. Given an array A[0]...A[n-1] of integers, find out the length of the longest ascending subsequence.
Assumptions
A is not null
ExamplesInput: A = {5, 2, 6, 3, 4, 7, 5}Output: 4Because [2, 3, 4, 5] is the longest ascending subsequence.**
方法一
O(n^2)
任意一个位置往前面看所有的数,找到比当前的数小的最大数的值M[j] + 1 (Math.max(M[i], M[j] + 1)
public class Solution {
public int longest(int[] array) {
// Write your solution here.
//using dp to solve this problem
//M[i] represents the longset ascending subsequence from 0 to i
//base case is the first element
//Input: A = {5, 2, 6, 3, 4, 7, 5}
// 1 1 2 2 3 4 4
int max = 1;
int[] M = new int[array.length];
if(array.length == 0){
return 0;
}
for(int i = 0; i < array.length; i++){
M[i] = 1;
for(int j = 0; j < i; j++) {
if(array[i] > array[j]){
M[i] = Math.max(M[i], M[j] + 1);
}
}
max = Math.max(M[i], max);
}
return max;
}
}
方法二:
从第0 个元素开始往数组里面插入元素, 如果往前找,如果能找到比插入的当前元素大的最小的元素,则用当前的元素替换掉那个数; 如果找不到,直接再数组后面插入这个数。返回数组长度
O(nlogn)
public class Solution {
public int lengthOfLIS(int[] nums) {
//step1: find the largest smaller number of int i;Using binary search
//{5,2,3,1,9,4,2,1,5,7,8}
// 1 2 4 5 7 8
if(nums.length == 0) {
return 0;
}
int[] M = new int[nums.length + 1];
M[1] = nums[0];//2
int result = 1;
for(int i = 1; i < nums.length; i++){
int index = largestSmaller(M, 1, result, nums[i]);//
if(index == result){
M[++result] = nums[i];
}else{
M[index + 1] = nums[i];
}
System.out.print(M[result] +",");
}
return result;
}
private int largestSmaller(int[] M, int left, int right, int target){
while(left <= right) {
int mid = left + (right - left)/2;
if(M[mid] >= target){
right = mid - 1;
}else{
left = mid + 1;
}
}
return right;
}
}
LC
**Given an array of 2D coordinates of points (all the coordinates are integers), find the largest number of points that can be crossed by a single line in 2D space.
Assumptions
The given array is not null and it has at least 2 points
Examples
<0, 0>, <1, 1>, <2, 3>, <3, 3>, the maximum number of points on a line is 3(<0, 0>, <1, 1>, <3, 3> are on the same line)**
在这里使用线的点斜式定义,遍历所有的点,找到每个点和其他所有点组成的线的斜率,若相等,则是在同一条线上,记录下斜率相同的pair个数。数据结构:使用hashMap来储存每个可能的slope
/*
* class Point {
* public int x;
* public int y;
* public Point(int x, int y) {
* this.x = x;
* this.y = y;
* }
* }
*/
public class Solution {
public int most(Point[] points) {
// Write your solution here.
int result = 0;
for(int i = 0; i < points.length; i++){
Point seed = points[i];
int same = 1;
int sameX = 0;
int most = 0;
HashMap cnt = new HashMap<>();
for(int j = 0; j < points.length; j ++){
if(i == j){
continue;
}
Point temp = points[j];
//斜率和截距都相等
if(temp.x == seed.x && temp.y == seed.y){
same++;
}else if(temp.x == seed.x){
sameX++;
}else{
//斜率相等,过同一点的直线上的点
double slope = ((temp.y - seed.y) + 0.0)/(temp.x -seed.x);
if(!cnt.containsKey(slope)){
cnt.put(slope, 1);
}else{
cnt.put(slope, cnt.get(slope)+1);
}
most = Math.max(most, cnt.get(slope));
}
}
most = Math.max(most, sameX) + same;
result = Math.max(result, most);
}
return result;
}
}