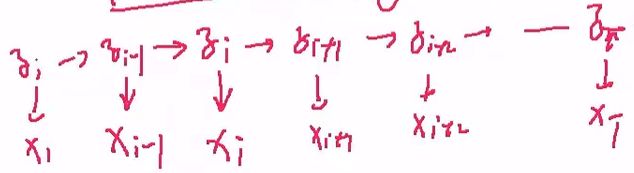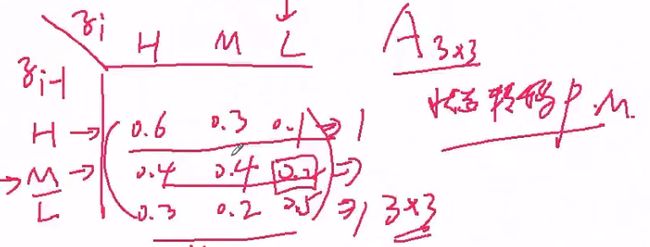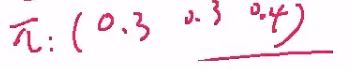课前问答
问：在主题模型中，PageRank，某个网页的重要度DP(i)是通过D(Pj)的重要度加权算出来的，那D(Pj)是如何计算的？
答：D(Pj)的重要度是将所有的网页的重要度随机初始化，然后迭代，当能收敛的时候，就认为结束计算了。
问：TextRank中的D(wj)是如何计算的？
答：
2019-02-20 14_50_37-机器学习第七期升级版.png
我们想求取文本相似度的时候，需要求取单词的重要度，需要给定窗口。假定窗口长度为10，我们认为窗口中的词都是有链接的。如果一个词重复出现，则它们的链接会越来越多。用这个D(w i)的计算公式，就能计算词的重要度。有了词的重要度，就能够使用交集数目，计算两个句子之间的相似度。两个句子的相似度有了，可以利用加权，获取句子的重要程度。
问：为什么感觉EM、LDA、HMM都有一个隐变量，这三个算法后面有什么暗中的联系或者共性么？为什么老师正好把这三个算法放在一块讲了？
答：EM算法确实是带有隐变量的，这是一个通用求隐变量的模型。
LDA，主题是我们观察不到的，也是隐变量。
但是EM，LDA，HMM并不是刻意的课程安排在一起，不过EM之前的内容，都是x直接得到y的，比如：随机森林，决策树，GBDT，逻辑回归，都是给定样本建模的过程，带隐变量的部分，偏难一些，所以放在后面了。
但是EM算法的一个实现版本:Baum-Welch算法，其实是对隐马尔科夫模型发展起到决定性的作用。
2019-02-20 17_13_37-机器学习第七期升级版.png
即红框中的算法。
而LDA也可以使用EM算法，进行参数学习。我们简单提了Gibbs采样，但是我们也提了变分EM算法，也是更快速的计算得来参数的。
现在发展出了很多在线学习算法，能够遍历一遍，就能得到结果，如Gensim中的实现。
这三个确实有一定联系，EM是算法基础，LDA和HMM都是两个贝叶斯网络，EM算法可以解决它们的求参问题。
问：很多书或论文上都说数据进一步处理前要去趋势，去周期，这是必须的么？
答：这要看时间序列，如果是的，确实需要做这个事情。
主要内容
我们想象一下，比如做事情时，考虑Logistic回归，模型为：
P(x|θ) = 1 / (1 + e -θ*x)得到的结果。这个是Logistic回归想解决的问题。
于是会引出三个问题：
- 概率计算
给定了某一个样本，X1，想计算X1属于哪一个类别，或者概率？
在θ已知的前提，将X1代入公式即得到概率。
2.参数估计
我们得到(x1, y1), (x2, y2), ..., (xm, ym)共m对样本，希望通过这么多样本，计算参数θ？即参数的估计问题。 - 模型预测
如果我们有一个估计的θ结果，对于新的样本，Xj，将其代入公式，即利用模型做预测，与概率计算差不多。
所以说Logistic回归，也是根据概率计算，参数估计，模型预测去做的，而HMM也是这个套路，但会复杂一些。
而且会花50%~60%的时间，用于说明概率计算。
隐马尔科夫模型的用途
中文分词，引申问题：实践问题应该如何建模？
先了解什么是马尔科夫模型
以天气为例
假定每天天气只有四种情况
sunny
windy
rainy
snow
并且我们认为天气的情况是随机变量，如：
x1, x2, x3, ..., xt
我们认为第一天天气对第二天天气是有影响的；第二天天气对第三天天气也是有影响的，同理，构成一个链路
x1 -> x2 -> x3 ... -> xt
则，P(xi-1, xi+1|xi) = P(xi-1|xi) * P(xi+1|xi)
这意味着，给定xi的时候，xi-1与xi+1是条件独立的。
这其实是一种假设。
根据这种模型，我们如果有足够多的数据，那么根据最后一天的情况，我们其实是可以预测之后的天气情况的。
当然，这个模型有些简单。
简单到了，这个模型拟合数据没那么多，我们希望将模型做复杂一些，做更细致的拟合。
还是x有这四种可能天气，有第i天的天气状况，可能由某种隐含的因素λ决定的
λi -> xi
这些因素，比如气压，气温，含水量，云高等等。
我们这里只考虑气压这种情况，气压包括：
high
medium
low
这三种情况，高气压大概率引起天晴，低气压大概率引起下雨，即气压与天气是有相关性的，并且我们认为第i-1天的气压会影响第i天的气压，而气压同时影响到同一天的天气状况。
即气压之间存在着链路，而天气之间也存在着链路，形成下面的样子。
而λ，即气压这条链路，构成了马尔科夫模型，而马尔科夫模型隐藏在我们观测值：天气之内的。
即我们能够观察到天气的情况，但是观察不到气压的情况。
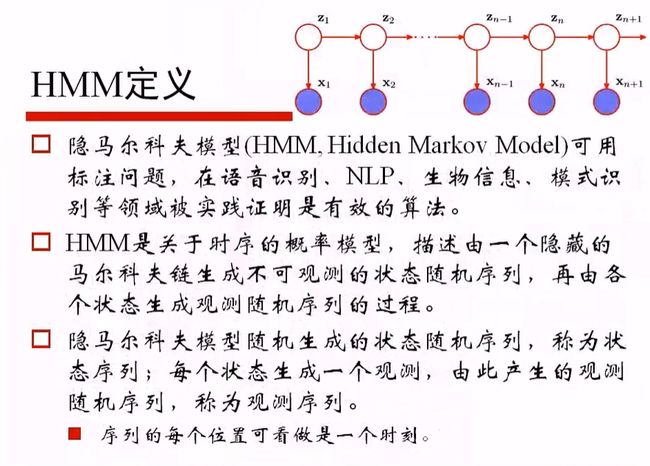
气压这条链路，所构成的马尔科夫模型，因为是隐藏的，所以又被称为隐马尔科夫模型，可以简写为"HMM"
天气的观测随机序列以及对应隐藏的气压状态可能为：
状态：H L H L H M M L L M H L L~~~~
观测：S S R R W S S S S W W R R ~~~~~
课题问答
如果有多个隐变量，在EM算法这种处理隐变量的算法里是怎么处理的呢？
答：一样可以求解。
2019-02-21 15_55_35-机器学习第七期升级版.png
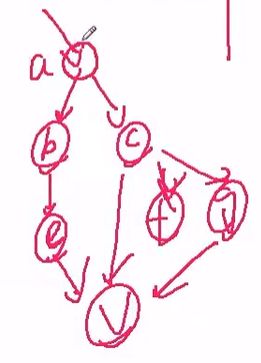
我们可以观测到a也可以观测到v，我们想得到其他节点，其发生概率，或者条件概率或者估计参数，其实就是我们建立的贝叶斯网络，也可以使用EM算法，一点点求：先得到总体的趋势，总体的每一个节点集合上的值，再得到每个具体的值。这个并不是深度学习，因为每个节点只是随机变量，与神经网络每个节点是神经元不同。
而贝叶斯网络很有可能与深度学习结合，因为贝叶斯网络是深度学习火爆之前，很重视的一个方向。
问：有没有某种办法确定隐变量是否存在呢？而不是事先假定隐变量存在？
答：这个没法确定，因为我们没有办法判定这种建模模式是否适合。只是因为处理过程中，发现第一好计算，第二有一定合理性，能够做一些预测，而且简单，就这么做了。其实到底是不是这样，很难讲。隐马尔科夫模型，是属于非常简单的贝叶斯网络了。
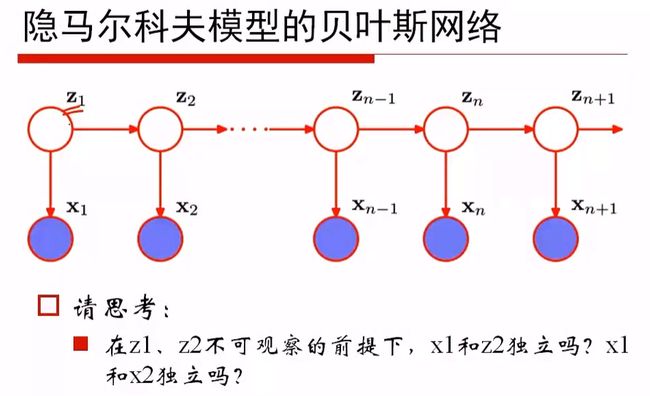
问：明面上的样本分布模型和HMM有关么？
答：如图，进行解释：
2019-02-21 16_04_43-机器学习第七期升级版.png
z1是未知的，x1与z2其实是相关的，不独立，z2与x2显然不独立，x1与x2自然也不独立。即建模方式，x1, x2, ..., xn+1其实是结构化数据，并不是随机序列。
所以说，凡是看到空间连续，时间连续的数据，就有可能尝试用隐马尔科夫模型做一些预测。
所以HMM的使用场景与之前提到的不一样，包括LDA，因为LDA也是认为样本是独立的
HMM的确定
依然以天气（预测）与气压（状态）作为场景：
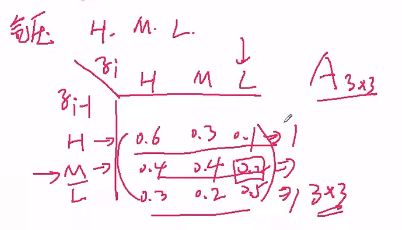
任何给定一个天气，比如气压: H, M, L，三种情况，下图说明前一天与今天的气压概率分布，而这个气压概率分布就是状态转移概率矩阵，其实就是隐状态之间的相互转移概率矩阵。
之前所述的阶层之间的变化，就是马尔科夫模型，它想做的就是状态转移，形成的状态转移概率矩阵
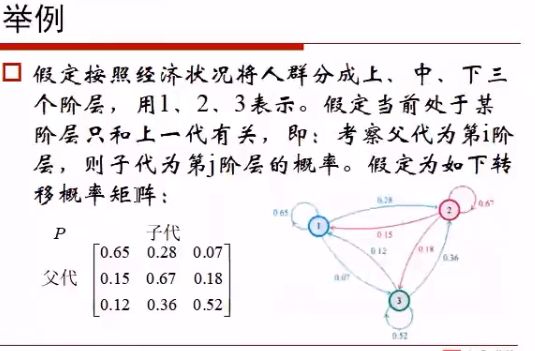
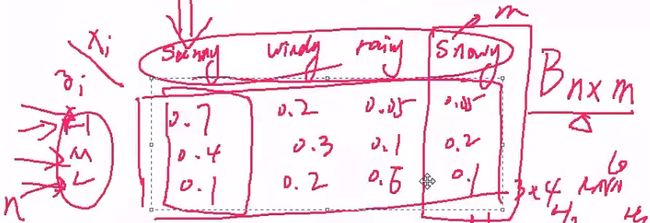
然后看第二种，当今天知道气压的时候，第i天的天气状况是什么呢？比如，sunny, windy, rainy, snowy，可以通过概率表示。
即B为nxm的矩阵，n为隐状态，m为观测值。B为观测矩阵，或者说发射矩阵，混淆矩阵。
所有的模型中，有z1 （见上图：隐马尔科夫模型的贝叶斯网络），初始情况，将z1拿出来，可能为气压的(H, M, L)中的某一个，其对应的概率为π(0.3, 0.3, 0.4)，即可以将A, B, π写在一块，构成：
λ = (π, A, B)，即描述隐马尔科夫模型的参数情况
问答
问：怎么感觉和LSTM很像呢？
答：不太像。只能说LSTM做连续值的计算，比如从X1想到的H1，需要得到前一天的状态H0参与计算，然后输出给下面的环节。
如图示：
2019-03-01 18_26_03-机器学习第七期升级版.png
其与隐性马尔科夫模型并不完全一样，因为隐性马尔科夫模型中的z1是随机变量，而LSTM是将模型中具体的样本数据喂进去。
有一定相似的感觉，但完全不一样。
隐性马尔科夫模型是贝叶斯网络；
LSTM模型是神经网络。
问：这个矩阵是根据历史值来定的么？
答：肯定是根据历史的数据计算。
问：B矩阵不需要保证每一列的和为1么？
答：因为我们这里只是保证其是状态转移概率矩阵，不需要它的列相同。如果B矩阵的列的值相加和>1，说明这个地区不管是各种情况（高气压，中气压，低气压）平均出现，其出现Sunny的概率，超过Snowy的概率。说明这个地方不容易下雪，非常容易天气。
所以完全不需要保证每一列和为1
问：转移矩阵是已知的么？
答：是否已知，需要根据样本来算。就是我们要想做结果，如果要计算预测值，必须已知。但是，如果建模的时候，只有样本，没有参数，需要根据参数计算值，还是要计算的
问：这些概率，样本固定了，不就固定了么？
答：是的，所以要说明的就是怎么求。
隐性马尔科夫模型的两个基本性质
举例，使用HMM建模，建模出某地区的气压以及天气状况
其中A为如下矩阵，即气压状态转移概率矩阵A：
B为如下矩阵，即气压与天气的状态转移概率矩阵B：
同时，我们也有了π向量，
问题：经过一段时间观察求，
第一天：sunny
第二天：sunny
第三天：windy
第四天：rainy
第五天: rainy
第六天: snowy
的联合概率，
即求P(sunny, sunny, windy, rainy, rainy, snowy)的联合概率，观测值为O：sunny, sunny, windy, rainy, rainy, snowy，求P(O|λ),其中λ为给定参数：A, B以及π，这是第一个问题，即：
- 求P(O|λ)
- 求P(λ|O)
如果经常长期的观测，得到大量的数据，（如观测10天数据 + 观测5天的数据 + 观测20天的数据 + ...）然后希望根据观测到的数据，估计P(λ|O)，即参数的估计或参数学习的问题。
可以这样考虑，计算给定λ的时候，哪一个λ可以使得P(O|λ)得到最大值，那么此时的λ就是我们所要求的，即maxλP(O|λ)，这个本质是最大似然估计，或者EM算法 -
P(I|O,λ)
假定已经求出来λ，使得P(O|λ)得到最大值，有新的一条观测数据O，我们想看看隐状态序列：P(I|O,λ)到底是什么
如，天气序列O为：Sunny Sunny Windy Rainy Windy Windy Rainy Sunny，这些天气各自对应的气压I(High, Middle, Low)是什么。
相当于根据已经观测到的数据，推导背后的隐变量，是将已经被混合的数据，重新解混出来(un-mix)，即对O进行解码。
上述三个问题，就是隐马尔科夫模型的主要作用，即what
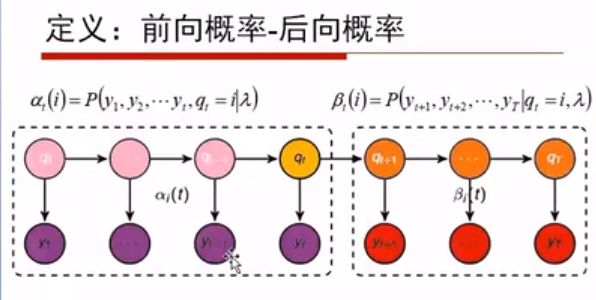
三个问题的PPT表述如下图：
2019-03-04 15_39_29-机器学习第七期升级版.png
2019-03-04 15_41_03-机器学习第七期升级版.png
直接计算
如何做概率计算呢？
因为根据λ直接求O不好算，所以需要加入隐状态随机序列I，并根据I求加和。
P(O|λ) = ΣIP(O, I|λ)
= ΣIP(O|I, λ) *P(I|λ)
= Σi1, i2,...itP(o1, o2, ..., ot|i1, i2, ..., it, λ) *P(i1, i2, ..., it|λ)
我们先看这一项：P(i1, i2, ..., it|λ)
令：P(i1, i2, ..., it|λ) = P(i1|λ)P(i2|i1, λ) P(i3|i2, λ)...P(it|i(t-1), λ)
因为Z1 = (π1, π2,..., πt)，所以
= πi1 Ai1i2Ai2i3...Ai(t-1)it
然后再看这一项：P(o1, o2, ..., ot|i1, i2, ..., it, λ)
P(o1, o2, ..., ot|i1, i2, ..., it, λ) = P(o1|i1)P(o2|i2)...P(ot|it)
P(o1|i1),即矩阵B中，隐变量气压与观测值天气的关联概率：
所以：
=Bi1o1Bi2o2...Bitot
所以：
P(O|λ) = Σ IP(O, I|λ)
= Σ IP(O|I, λ) *P(I|λ)
= Σ i1, i2,...itP(o1, o2, ..., ot|i1, i2, ..., it, λ) *P(i1, i2, ..., it|λ)
= Σ i1, i2,...itπ i1 A i1i2A i2i3...A i(t-1)it * Bi1o1Bi2o2...Bitot
因为A, B, π，都是已知的，i1, i2到it，总是可以遍历的。所以说，我们刚才所要的P(O|λ)就能够求解了。
更直观的如下图：
时间复杂度是指数级别的，其实不堪用：
问答
问：难道是主题模型+主题下词分布么？
答：有点这个感觉
问：隐马尔科夫模型解决的问题可以用RNN解决么？有没有可能被RNN相关模型取代呢？
答：有。隐马尔科夫模型解决的是一个时间序列问题，RNN解决的也是一个时间序列问题。今天我们更关注通过RNN解决时间序列问题。但是即使如此，不排除一些领域，使用HMM的效果就已经不错了，比如中文分词。
问：求出的应该是一个隐变量吧，如果有多个隐藏因素的话，能否再细分？
答：可以通过隐马尔科夫模型求出多个隐变量，比如刚刚的例子，除了气压之外，还可以加入云量等隐变量。
问：这是概率链式法则么？
答：谈不上，这是暴力求解
问：π是什么？
答：π是Z值，即隐变量，本例为气压，π1，即是第一天高气压，中气压，低气压的概率分布，如π: (0.3, 0.3, 0.4)
问：暴力求解是把所有的结果都求出来么？计算量很大
答：是的
问：求解目标是给定λ计算O，但是在求解过程中又把O的概率当做已知条件，这岂不是矛盾了么？
答：并没有。我们求的是，第t天的，样本的似然概率。因为已经知道了π，A，B，所以显然是可以求的。O1, O2, O3...Ot序列本身是已经知道的，但是不知道其发生概率。
问：A矩阵是隐变量的转移矩阵吧？可是隐变量是无法观测到的，怎么能用呢？
答：隐变量是无法观测的，但是状态转移矩阵，我们是可能从某种算法算出来。
问：这样乘出来是一个很小的浮点值吧？有啥作用？
答：我们会通过某种方案将其算出来。我们可以用来求，比如取对数。
优化算法
如果计算的时间成本太高，可以通过如下方式进行优化，也就是所谓的动态规划的方法：
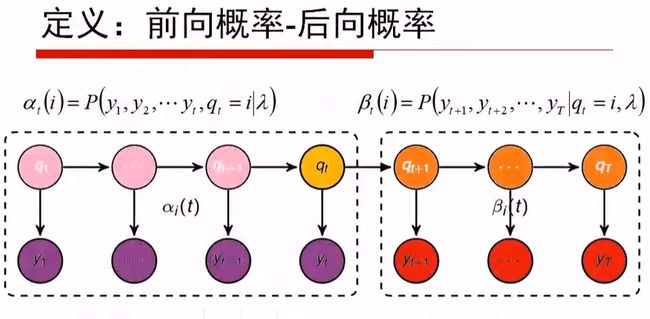
即αt(i) = P(o1o2...ot, qt=i)
当t=1，则P(o1, qi=i)=P(o1|q1=i)*P(q1=i)
而P(q1=i)与πi是等价的。
P(o1|q1=i)的发射概率为Bio1
所以t=1时，P(o1, qi=i) = Bio1 * πi
也就是我们所写的，下图中的初值
当我们想计算αt+1(i)，其概率是什么？
我们想去让第t个时刻：αt(j)在什么状态上呢？不知道，也无所谓，但是我们需要让第t个时刻的状态j，转移到状态i，并且让它的j号隐状态，从1到n做加和，即：
αt+1(i) = （Σj=1nαt(j)aji)*Bio(t+1)
其中αt+1(i)，我们观测从o1, o2, ..., o(t+1)，而右侧：（Σj=1nαt(j)aji)，我们观测从o1, o2, ..., o(t)
Bio(t+1): 是t+1个时刻，从i隐状态观测到o(t+1)的发射概率。
这个就是状态概率转移矩阵。
最终：
αT(i) = P(o1, o2, ..., ot, qt=i)
当Σi=1nP(o1, o2, ..., ot, qt=i)时，qt=i积分积没了，就只剩下Σi=1nP(o1, o2, ..., ot)，所以：
P(o1, o2, ..., ot) = Σi=1nP(o1, o2, ..., ot, qt=i)
或者简写为：
P(O|λ) = Σi=1nαT(i)
问答
问：发射概率是什么？
答：即观测概率，混淆概率或混淆矩阵
B t(i)指的是，第t个时刻，让它位于第i号隐状态的前提下，我们观察到后面所有值的观测概率。
想计算O的第t个时刻，对第i个隐状态的联合概率：即前向概率与后向概率的乘积，要求位于同样时刻，同样隐状态
因为P(q t=i, O|λ) = α t(i) * β t(i)，所以可以得到：
P(q t=i|O,λ) = P(q t=i, O|λ)/P(O|λ) =( α t(i) * β t(i) )/Σ i n(α t(i) * β t(i))
求P(q t=i|O,λ)的值的意义在哪呢？
因为：我们的O，即o1, o2,..., ot已经存在了，换句话说我们已经观测到了天气情况，如Sunny Sunny Windy Rainy Rainy Windy这么一个序列。
我们可以计算t=1的时候，隐变量，即气压是高、中、低的概率，这个三个概率，通过上述公式就能求解计算。
因此这三个概率，谁最大，我们就认为其背后的隐变量是哪个，比如低气压概率最大，那么低气压就是隐状态。
每个值分别做计算，就能得出隐变量分布，如：
Sunny Sunny Windy Rainy Rainy Windy(观测序列), 算出气压的:
Low High Middle Middle High Low High(状态序列)
γ的意义
学习算法
问答
问：P(q, o)与前向概率有区别么？
答：P(q, o)指的是P(qt=i, O|λ) ，不是前向概率，等式指的是同一个时刻，前向概率与后向概率的乘积，但是其定义是，第t个时刻等于i的同时，观测到的o1, o2,..., ot的联合概率。并不是前向算法。
问：状态转移概率是怎么求的？
答：其实是用学习的算法进行求解。
问：P(q, o)与P(o, q)的区别？
答：P(qt=i|O)，这个是可以求解的；而P(O|qt=i)这个是无法求解的。意义上是想计算：第t个时刻，位于i的隐状态上，得出o1, o2,..., ot的联合概率。得到所有的隐状态，是可以求的；但是只有一个隐状态i，是无法求的。
问：递推公式的加和是什么意思？
答：
2019-03-05 16_44_39-机器学习第七期升级版.png
应该是问的这个公式中的加和。我们想计算第t+1个时刻的时候，它现在的某种位于第i号状态上的某种概率。但是i号状态怎么来的呢？它一定是前一个时刻，位于任何一个状态上，转移过去的。
如果前一个时刻位于j号上，后一个时刻位于i号，j是什么根本不关心，因此令j从1到N做遍历，最后都能转移到i号上。
所以有Σ这个加和。
问：前向算法求红白红，为啥乘的概率是0.5,0.4,0.7，第28页
答：问的问题如图：
2019-03-05 16_50_45-机器学习第七期升级版.png
π，我们都清楚，O的解释：o1：红，o2：白，o3：红, B矩阵，第1列是红，第2列是白。其实就是代公式的过程。
问：为什么计算的过程中没有π了？
答：因为只有初值才使用到π，而初值是参与后续计算的，其实π是有的。
2019-03-05 16_56_37-机器学习第七期升级版.png
问：前向算法中间P(O,I|λ) = P(O|I,λ)*P(I|λ)没理解
答：P(O, I) = P(O|I)*P(I)，这个几乎是条件概率的定义。既然如此，P(O, I|λ)=P(O|I,λ)*P(I|λ)，这个式子就是这样推算的。
问题：如果想做中文分词，该怎么做？
我们给定任何一个句子，进行切词。
我们可以定一任意一个汉字为两种隐状态。
- 这个汉字为所在词的最后一个字
- 这个汉字不是所在词的最后一个字
这个构成了状态序列的可能取值：Q:{End, not End}
观测序列为：如果是unicode编码，其为216，
即V:{0, 1, 2, ..., 65535}
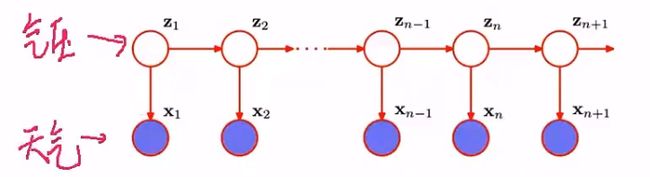
现在考虑这个隐马尔科夫模型的时候，相当于：
即观察到的字（对应下方的y序列），它们对应的隐状态可能是终止字，可能不是终止字。
即构成了状态序列的可能取值: Q: {end, ^end}
观测序列是UNICODE编码，V: {0, 1, 2, ..., 65535}
我们观察文字，第一个字是否是终止字，是与之后的字有状态转移关系的。
如i-1的时刻可能是终止字也可能不是终止字
i的时刻，可能是终止字也可能不是终止字
构成一个2x2的状态转移概率矩阵：
0.1 0.9
0.3 0.7
假定根据终止字与非终止字，各为一行；
汉字0~65535各为一列，
则构成了2x65536的观测矩阵B。
此时设一个π(π end, π ^end)
则模型就有了，这就是所谓的参数求解过程，即得到：
(π, A, B)
然后根据这个模型，对新的句子做分词。
下面讲讲分词学习的过程。
比如下图这个已经做好分词的文本：
我们现在想对这个数据求解π，A，B
实际当中，获取Begin, Middle, End, Single四种隐状态
比如总书记，总: Begin, 书: Middle, 记: End
我：单字成词，Single
π: 将每个句子的第一个字取出来，然后判断是属于Begin, Middle, End还是Single，然后构成一个列表
A: 首先考虑B M E S构成4x4的矩阵：
B M E S
B
M
E
S
然后按照one-gram移动，得到两两匹配，比如中国 政府，中与国属于BE,国与政构成EB，政与府构成BE
然后按行做归一化，得到A
B：为4x65536的矩阵
0 1 2 3 4 ... 65535
B
M
E
S
然后逐字填入矩阵，按行做归一化，B就做完了。
这样就完成了参数学习。
公式就能体现出上面的说法：
无监督的算法
这个有一丢丢难，是用EM算法做的，而且效果不堪用