[ 阅读这篇文章你需要花3-5分钟的时间,但你可从运用中受益的时间可能为一生。]
博弈论(Game Theory) 又被称为对策论(Game Theory),它是现代数学的一个新分支,也是运筹学的一个重要组成内容。《博弈圣经》中写道:博弈论是二人在平等的对局中各自利用对方的策略变换自己的对抗策略,达到取胜的意义。
博弈论就是研究互动决策的理论,所谓互动决策,即各行动方(即局中人[player])的决策是相互影响的,每个人在决策的时候必须将他人的决策纳入自己的决策考虑之中,当然也需要把别人对于自己的考虑纳入考虑之中……在如此迭代考虑情形进行决策,选择最有利于自己的战略(strategy)。
所以呢,博弈论的基本概念包括局中人、行动、信息、策略、收益、均衡和结果等。其中,局中人、策略和收益是最基本要素;局中人、行动和结果被统称为博弈规则。
- 1 -
上次我们聊电车实验时,提到了一个词“零和博弈”,那么今天要讲的囚徒困境则是博弈论的非零和博弈中具代表性的例子。
与零和博弈相区别,在非零和博弈中,对局各方不再是完全对立的,一个局中人的所得并不一定意味着其他局中人要遭受同样数量的损失。也就是说,博弈参与者之间不存在“你之得即我之失”这样一种简单的关系。其中隐含的一个意思是,参与者之间可能存在某种共同的利益,蕴涵博弈参与才“ 双赢”或者“多赢”这一博弈论中非常重要的理念。
比如,在恋爱关系中,有可能是一方受伤,另一方并不是一定得到满足;也有可能双方一起能得到精神的满足;也有可能双方一起受伤。一般而言,这种精神的损益不是零和的。
1950年,就职于兰德公司的梅里尔·弗勒德和梅尔文·德雷希尔拟定出相关困境理论,后来由顾问艾伯特·塔克(Albert Tucker)以囚徒方式阐述,并命名为“囚徒困境”。
囚徒困境是这样的:两个共谋犯罪的人被关入监狱,不能互相沟通情况。如果两个人都不揭发对方,则由于证据不确定,每个人都坐牢一年;若一人揭发,而另一人沉默,则揭发者因为立功而立即获释,沉默者因不合作而入狱十年;若互相揭发,则因证据确实,二者都判刑八年。
于是,每个囚徒都面临两种选择:坦白或抵赖。
那大家可不就乐了,哎你这困境算啥困境?如果两人都抵赖,各判一年,那不就最好咯?是这样吗?
但是,仔细分析,你会发现,不管另一个囚犯也就是你的同伙他会选择什么,你的最优选择都是坦白,他也是如此。
如果同伙抵赖、自己坦白的话放出去,抵赖的话判一年,坦白比不坦白好;如果同伙坦白、自己坦白的话判八年,比起抵赖的判十年,坦白还是比抵赖的好。结果,两个嫌疑犯都选择坦白,各判刑八年。
虽然说,如果两人都抵赖,各判一年,这个结果更好。但它不能满足人类的理性要求。由于囚徒无法信任对方,因此倾向于互相揭发,而不是同守沉默。囚徒困境所反映出的深刻问题是,“人类的个人理性有时能导致集体的非理性——聪明的人类会因自己的聪明而作茧自缚。”
囚徒们彼此合作可为全体带来最佳利益(无罪开释),但在消息不明的情况下,因为出卖同伙可为自己带来利益(缩短刑期),也因为同伙把自己招出来可为他带来利益,因此彼此出卖虽违反最佳共同利益,但这反而是自己最大利益所在。
洛思:主要是坦白和抵赖的己方期望收益相差太大。系统内的问题,不破局就无解。这就好比樊胜美妈妈只知道压榨女儿贴补儿子,而没有让儿子自己造血的认知。
- 2 -
下面,我们可以引进一个新概念——“蜈蚣博弈”。
囚徒困境里讲到了坦白和抵赖,即合作和背叛,因此,有必要引出蜈蚣博弈,这是由罗森塞尔提出的。
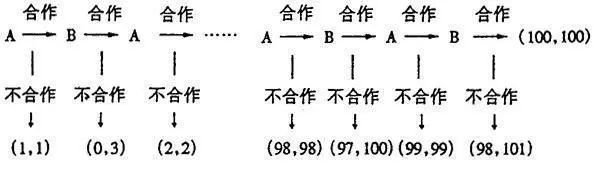
它是这样的一个博弈:两个参与者A、B轮流进行策略选择,可供选择的策略有“合作”和“背叛”(“不合作”)两种。假定A先选,然后是B,接着是A,如此交替进行。当然,A、B之间的博弈次数规定为有限次,比如,100次。
比如,我和某位朋友轮流选择合作。第一次,我会选择合作;第二次,他先选,他心想:第一次合作不错啊,继续合作吧。于是他选择合作。所以我们就一直合作,合作,合作,合作,合作……从1一直到97,98,99.
然而,到第100次的时候,他烦我了,想背叛我 (凉凉),他在心里算计着下一次不合作的话他可以和另一位商家合作,这样,他的收益会比和我选择合作的收益来得大。所以,在第100次选择的时候,他背叛了我。
也就是说,我们假定这个博弈如下:
选择:合作 合作 合作 合作...合作 合作
收益:A B A B …… AB (100,100)
选择:合作 合作 合作 合作...合作 背叛
收益:A B A B …… AB (98,101)
现在的问题是:A、B是如何进行策略选择的?
这个博弈因形状像一只蜈蚣,而被命名成“蜈蚣博弈”。
问题来了。
当A决策时,他考虑博弈的最后一步即第100步;B在“合作”和“背叛”之间作出选择时,因“合作”给B带来100的收益,而“ 不合作”带来101的收益,根据理性人的假定,B会选择“背叛”。
但是,要经过第99步才到第100步,在99步,A考虑到B在100步时会选择“背叛” ——此时A的收益是98,小于B合作时的100,那么在第99步时,他的最优策略是“背叛”——因为“背叛”的收益99大于“合作”的收益98……
咦!这就很奇怪啦。这是说明一开始就可以不要合作吗?
所以,是倒推法错了?还是直觉错了?这就是蜈蚣博弈的悖论。据说,这悖论有很多博弈专家都在寻求它的答案。
因为从现实出发,我们采取合作策略是好的。而从逻辑的角度看,也就是根据这个倒推法来看,一开始A应取不合作的策略。
当然,实验发现,不会出现一开始选择“不合作”策略而双方获得收益1的情况。双方会自动选择合作性策略,从而走向合作。这种做法违反倒推法,但实际上双方这样做,要好于一开始A就采取不合作的策略。
但是,我们也迟早有一天会“背叛”!理性的人会出于自身利益的考虑,在某一步采取不合作策略。所以倒推法肯定在某一步要起作用,这个时候,合作便不能进行下去。
为什么囚徒困境和蜈蚣博弈是相关联的呢?
在囚徒困境中,如果两个囚徒都在第一局保持沉默,以期望建立互信关系,从而最终都能很快被释放,那么他们双方都会保持沉默。
但是,警察哪有那么好说话哦。他肯定还会再来审问你们。因此,在第二局,双方亦应有相似的想法,继续保持沉默,以期继续在互信的情况下进行第三局,以致余下的八局。这也是合理的。
但是呢,在第十局时,互信的关系明显是没有意义的,因为十局已经完结,囚徒没有必要为维持互信的关系而沉默(没有第十一局),所以第十局囚徒一定会背叛对方的,理由和只有一局囚徒困境一样。
那既然大家都知道在第十局,无论如何对方都会背叛自己的,你在第九局保持沉默也是没有意思的,要知道,保持沉默(友好关系)的原因是为了希望下一局对方还能保持沉默。所以,第九局,双方都一定会背叛对方的。那么,第八局,第七局不也是这样吗?
如此类推,十局都会互相背叛,所以他们是不可能建立起完全的互信关系的。
只有在囚徒困境的局数大家都不肯定的情况下,上述的推论才不会发生。
- 3 -
蜈蚣博弈在现实中都有哪些应用?
这里有一个来自知乎的回答,作者为王海。
来源:
https://www.zhihu.com/question/29543850/answer/68645077
蜈蚣博弈很简单,我举个实际运用的例子即可。历史上的三国鼎立和孙刘联盟就是最典型的蜈蚣博弈。孙刘联盟的博弈背景如下:
公元208年,刘备和孙权联盟对抗曹操。联盟维持时间越长,对孙刘两家越有利。但是孙刘联盟必不能长久,其中有个争议问题,就是荆州。
孙权和刘备都可以选择直接撕破脸皮强占了荆州,这样会让联盟立刻破裂;他们也可以选择搁置争议,让联盟维持下去。但是如果刘备在荆州经营越久,孙权就越没机会要回荆州。不妨假设如果双方一直合作,经过20年之后,孙权就永远要不回荆州了(这个时间换成30年,40年都不影响结论)。
这时博弈者孙权想了,我在20年之后要不回荆州了,太亏了,那我干脆在第19年的时候撕破脸皮,直接抢了荆州算了。孙刘联盟维持19年足够打败魏国了。
另一位博弈者刘备也想了,我感觉孙权这货在第19年的时候肯定会撕破脸皮,那我何不先下手为强,在第18年的时候翻脸。18年联盟时间足够打败魏国了。
孙权又想了,我感觉刘备会在18年的时候肯定会先下手为强,那我何不在第17年直接撕破脸皮。17年联盟时间足够打败魏国了。
这样一直博弈下去。
直到孙权想了,我觉得孙刘联盟要解除曹操的威胁,需要最少维持11年。至少在11年前,刘备不敢和我翻脸。那11年一到,我立刻翻脸让吕蒙夺了荆州吧。
刘备因为是博弈中优势的一方(实际控制荆州), 行动必然比孙权保守,觉得孙刘联盟最少需要维持十三四年,彻底拿下襄樊之后,才能解除老曹的威胁。于是决定在第14年翻脸。
由于孙权比较激进,所以最终先下手为强,在公元219年直取荆州。孙刘联盟破裂,两败俱伤。让还未大损元气的魏国捡了便宜。
实际上孙刘联盟最优决策是,两边一起先灭了最强的魏国,再一决雌雄。但是孙权不能接受这个安排,因为等灭掉魏国,荆州就拿不回来了,这样和刘备争霸胜算就很小了。于是就导致了蜈蚣博弈的出现。最后孙权只能冒险在时机尚未成熟的时候破坏了孙刘联盟,抢了荆州。
蜈蚣博弈就是两个合作者之间先下手为强的博弈。在不赔本的情况下,先撕破脸皮的人占便宜。因为合作双方都非常着急抢先动手,所以在这种博弈中,只有两败俱伤这一种可能的结果。
也就是说在三国的博弈中,吴蜀的悲剧在借荆州的时候就已经注定了,最有可能笑到最后的一定是魏国。如果你是孙权,你会发现你别无选择,不抢在刘备之前撕破脸皮夺回荆州,你将永远是刘备的垫脚石。如果你是刘备,你会发现你不得不借荆州,要不然你就会变成博弈中的孙权。
另外,你们知道为什么这个回答下只有我举出来了现实例子,而其他答主举得都是什么海盗分金币一类的虚构例子吗?因为我这个三国的例子是不完全信息的蜈蚣博弈,也就是说刘备和孙权互不知道对方底线。而博弈论教科书为了方便初学者理解,讲的都是完全信息的蜈蚣博弈,这种博弈从一开始就崩溃了,因为双方根本不会参加这种博弈。比如如果刘备一开始就知道孙权第11年会撕破脸皮,而自己的底牌是14年,那这个博弈在谈判阶段就谈崩了。从一开始就不会有联盟这回事。
- 4 -
所以,博弈论有点像一环扣一环吧,生活中哪个不是一环扣一环呢?
想一想,在现实中,我们是不是很少会在开始时确定策略为“不合作”呢,但是又确实难以确定在何处采取“不合作”的策略?
洛思:这是“回路”设定的问题。执着于一兵一卒,短期收益反馈良好,大局却是满盘皆输。现实生活中短期收益的半衰期很短,而长期收益的半衰期很长,甚至可以说短期收益往往是迅速折旧的,而长期收益往往是复利增长的。
因此,在实际情况中,我们要搞清楚的是对方什么时候结束,永远比他先结束的同时还要考虑利益最大化。
蜈蚣博弈还演变出来了倒推法,它的原理就是计算每一个环节的得失,最后推出当下的最优策略。这样的博弈或者说是思想吧,在我们生活中真的很常见。
一对恋人在一起,一开始算是“合作”关系,双方都有收益,计为1。在这之后,每个月的相处、每一年的相处都算是我们合作关系的累加,得益也会因此而增加。但是两个人在一起总会吵架吧?吵架多了或者遇到啥大事了总会想分手吧?如果女生没多久就选择分手,那么她的得益是2,而男生是0。
但如果一开始我选择继续,你也选择继续在一起,那么每一轮博弈之后我们双方得益均为1,一直持续下去得益就会一直增加,啊也就是感情会越来越好啦。如果最终会分手,按得益来讲,那分手的那一个终归会比被分手的人收获更多一点。
如果我和你在两年后会分手,那我为了不被你甩,我会提前1个月和你提出分手;当然,同样的,你知道我会提分手,于是你又要提前一个月和我说分手。以此类推呢,在很早的时候,我们就已经在心里选择了“背叛”。
“反正我们也迟早会分手。”
“长痛不如短痛。”
洛思:又比如,第1天早起跑步的收益是10,对应的修仙+睡懒觉的收益可能是20。那么从这天看最佳策略是修仙而不是晨跑。然鹅到了第二天,晨跑的收益变成10.2,而修仙的收益折旧为19.6……以此类推,第21天晨跑的收益增至15.16,而修仙的收益降为13.09。 开始的最佳策略是修仙,而终局的最佳策略则是晨跑。
P:我觉得我们大学生实习或者毕业后选择去什么样的公司实习也可以利用到这样的思想。A公司短期可以给你高薪,但是对你的发展不太有帮助;B公司暂时给不了A公司那么多薪资,但是给你留的发展空间是很大的。那你在选择的时候就有必要去比较短期和长期收益了。不要因为暂时的享乐,就不考虑自己的未来。除了当下看起来不错的回报,更要思考一个问题——我当下所做事情,对我五年十年后的事业有什么重大意义吗?做正确的事情,比把事情做正确更重要。
那么在这样一个蜈蚣博弈的困局里,我们要如何来破呢?
1.建立信任
毕竟这个博弈是合作或是背叛嘛,而合作的基础则是信任。因此,在这样一个关系中,我们要先学会建立对彼此的信任。要找投资,ok,那你要让对方信任你,给你投钱,你也要信任对方,开诚布公。和爱人在一起,你要互相信任吧,少一点怀疑,多一点爱。
2.有所行动
在这样的关系中,要让对方信任你并且和你合作,你就要有行动去证明你的可以让他信任的,要多付出一些,而非斤斤计较。否则,合作关系很快就会停止。这里的合作可不一定指企业合作啥的这种哟,而是指一种关系。合资方可以说是合作,爱情可以说是合作,友情和亲情亦可以说是合作关系。
3.最优选择能力
这个思维能力很重要,即你要去思考短期利益和长期利益,并且辨明在当下,你应该选择什么样的选项可以让你获得最大收益。
根据这个可以延伸出来的是,我们应如何与人相处。我们常说“吃亏是福”,就是指在与他人的合作关系中,不要太计较自己是不是太吃亏,不要太精明,而应该学会如何建立好合作关系,和人长期合作下去,从而真正获得精神和物质上的最大得益。学生时代如此,步入社会更是如此。