回溯算法经典例子

---

基本思想

有许多问题，当需要找出它的解集或者要求回答什么解是满足某些约束条件的最佳解时，往往要使用回溯法。回溯法的基本做法是搜索，或是一种组织得井井有条的，能避免不必要搜索的穷举式搜索法。这种方法适用于解一些组合数相当大的问题。
回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。
解空间树：
例如，对于 n=3 的 01-背包问题，可以用完全二叉树表示其解空间：

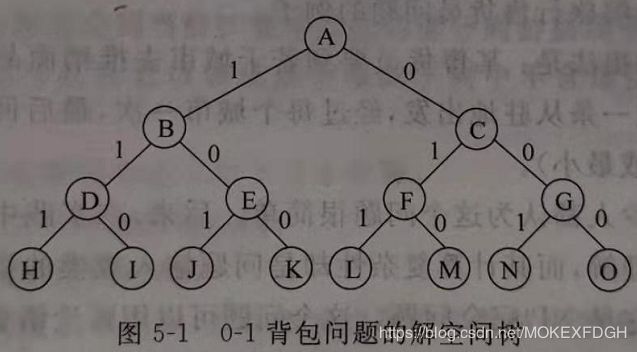
解空间树的类型

1. 子集树：当所给问题是从 n 个元素的集合 S 中找出 S 满足某种性质的子集时，相应的解空间树称为子集树。

		void backtrack(int t){
			if(t>n)
				output(x);
			else{
				for(int i=0;i<=1;i++){
					x[t] = i;
					if(constraint(t)&&bount(t))
						backtrack(t+1);
				}
			}
		}

2. 排列树：当所给问题是确定 n 个元素满足某种性质的排列时，相应的解空间被称为排列树。

		void backtrack(int t){
			if(t>n)
				output(x);
			else{
				for(int i=t;i<=n;i++){
					swap(x[t],x[i]);
					if(constraint(t)&&bount(t))
						backtrack(t+1);
					swap(x[t],x[i]);
				}
			}
		}

回溯的过程：

1. 回溯法从根节点出发，以深度优先方式搜索整个解空间。
2. 这个开始节点成为活结点，也成为当前的扩展结点。在当前扩展结点处，搜索向纵深方向移至一个新结点，则这个新结点成为新的活结点，并成为当前的扩展结点。
3. 如果当前扩展结点不能再移动，则当前扩展结点成为死结点，此时应该回溯到最近的活结点处。
4. 直到在解空间中已无活结点则搜索结束。

解题的步骤：

1. 针对所给问题，定义问题的解空间
2. 确定易于搜索的解空间结构
3. 以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索

---

批处理作业调度

问题：给定 n 个作业的集合 J={J1,J2,…,Jn}，每个作业 Ji都有两项任务分别在两台机器上完成，每个作业必须先有机器1处理，然后由机器2处理。Fji 是作业 i 在机器 j 上完成处理的时间。所有作业在机器2上完成处理的时间和称为该作业调度的完成时间和，批处理作业调度即给出最优调度使得完成时间和最小。

解题思路：
可以确定解空间是一颗排列树，设 x=[1,2,…,n] 是所给的 n 个作业，则相应的排列树由 x[1:n] 的所有排列构成。

• 当i>n时，算法搜索至叶子结点，得到一个新的作业调度方案。此时算法适时更新当前最优值和相应的当前最佳调度。
• 当i

代码：

		public class FlowShop{
			static int n,f1,f,bestf;
			//作业数，机器1完成时间，完成时间和，最优值
			static int[][] m;//各作业所需的处理时间
			static int[] x;//当前作业调度
			static int[] bestx;//当前最优调度
			static int[] f2;//机器2完成时间

			private static void backtrack(int i){
				if(i>n){
					for(int j=1;j<=n;j++){
						bestx[j] = x[j];
					}
					bestf = f;
				}else{
					for(int j=i;j<=n;j++){
						f1 += m[x[j]][1];
						f2[i] = ((f2[i-1]>f1)?f2[i-1]:f1) + m[x[j]][2];
						f += f2[i];
						if(f<bestf){
							swap(x,i,j);
							backtrack(i+1);
							swap(x,i,j);
						}
					}
				}
			}
		}

---

符号三角形问题

问题：由14个“+”号和14个“-”号组成的符号三角形。2个同号下面是“+”号，2个异号下面是“-”号。

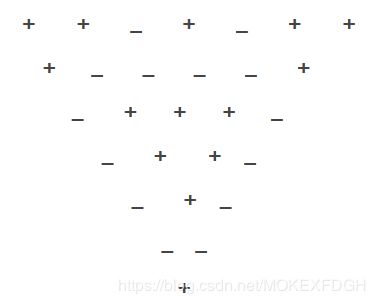
在一般情况下，符号三角形第一行有N个符号，该问题要求对于给定n计算有多少种不同的符号三角形。使其所含的+ — 个数相同。

解题思路：
用 x[1:n] 表示符号三角形的第一行的 n 个字符

• x[i] =1 时，符号三角形的第一行的第i个符号为+
• x[i] =0时，表示符号三角形的第一行的第i个符号位-
• 共有i(i+1)/2个符号组成的符号三角形。
• 确定x[i+1]的值后，只要在前面确定的符号三角形的右边加一条边就扩展为x[1:i+1]所相应的符号三角形。
• 最后三角形中包含的“+”“-”的个数都为i(i+1)/4，因此搜索时，个数不能超过…若超直接可以剪去分枝。
• 当给定的n(n+1)/2为奇数时，也不符合三角形要求。

代码：

		public class Triangles{
			static int n,half,count;
			//第一行符号个数，n*(n+1)/4。当前“+”个数
			static int[][] p;//符号三角形矩阵
			static long sum;//符号三角形个数
			
			public static long compute(int nn){
				n == nn;
				count = 0;
				sum = 0;
				half = n*(n+1)/4;
				if(half%2==1)
					return 0;
				half = half/2;
				p = new int[n+1][n+1];
				for(int i=0;i<=n;i++){
					for(int j=0;j<=n;j++){
						p[i][j] = 0;
					}
				}
				backtrack(1);
				return sum;
			}
			
			private static void backtrack(int t){
				if(count>half || (t*(t-1)/2-count>half))
					return;
				if(t>n)
					sum++;
				else{
					for(int i=0;i<=2;i++){
						p[1][t] = i;
						count += i;
						for(int j=2;j<=t;j++){
							p[j][t-j+1] = p[j-1][t-j+1]^p[j-1][t-j+2];
							count += p[j][t-j+1];
						}
						backtrack(t+1);
						for(int j=2;j<=t;j++){
							count -= p[j][t-j+1];
						}
						count -= i;
					}
				}
			}
		}

---

N 皇后问题

问题：在n×n格的国际象棋上摆放n个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

解题思路：
用 x[1:n] 表示 n 后问题的解，x[i] 表示皇后 i 放在棋盘的第 i 行的第 j 列。不同列，则 x[i] 都不相同。斜线上不能相同即，对于两个皇后(i,j) 和 (k,l)，|i-k| =/= |j-l|。

• 当 i>n 时，得到一个新的 n 皇后不被攻击放置方案，sum++。
• 当 i<=n 时，检查可行性，深度优先搜索可行子树。

代码：

		public class NQueen{
			static int n;//皇后个数
			static int[] x;//当前解
			static long sum;//可行方案数

			public static long nQueen(int nn){
				n = nn;
				sum = 0;
				x = new int[n+1];
				for(int i=0;i<=n;i++){
					x[i] = 0;
				}
				backtrack(1);
				return sum;
			}
			private static boolean place(int k){
				for(int j=1;j<k;j++){
					if((Math.abs(k-1)==Math.abs(x[j]-x[k])) || (x[j]==x[k]))
						return false;
				}
				return true;
			}
			private void backtrack(int t){
				if(t>n)
					sum++;
				else{
					for(int i=1;i<=n;i++){
						x[t] = i;
						if(place(t))
							backtrack(t+1);
					}
				}
			}
		}

---

0-1 背包问题

在动态规划中有问题描述以及动态规划的解题方法，这里只讨论回溯法的解法。

解题思路：
可用子集树来表示解空间，在搜索空间树时，只要其左儿子结点是一个可行点就进入，而右儿子只有在可能包含最优解时才进入，否则剪枝。

伪代码：

		static double c;//背包容量
		static int n;//物品数
		static double[] w;//重量
		static double[] p;//价值
		static double cw;//当前重量
		static double cp;//当前价值
		static double bestp;//最优价值

		private static void backtrack(int i){
			if(i>n){
				bestp = cp;//保存最优值
				return;
			}
			if(cw + w[i] <= c){//搜索左子树
				cw += w[i];
				cp += p[i];
				backtrack(i+1);
				cw -= w[i];
				c[ -= p[i];
			}
			if(bound(i+1)>bestp)//判断右子树的价值有没可能超过左子树
				backtrack(i+1);//超过则进入右子树
		}

---

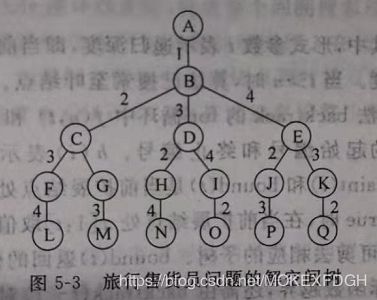
旅行售货员问题

问题：售货员要到n个城市去推销商品,已知各城市之间的路程（代价）a[][]，试选择一条路，从第一个城市出发经过每个城市一遍，最后回到出发城市所耗费的代价最小。

解题思路：
分析可知解空间是一棵排列树，每一条从根节点到达叶子结点的路径代表了n个顶点的一种排列。定义x[n]记录可行解。
剪枝函数：两个城市之间是否连通，到达当前为止的代价是否已经超过了最优代价，当前城市是否已经走过。