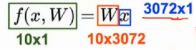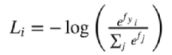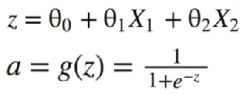深度学习之---从线性分类到人工神经网络

主要内容

背景介绍

• 深度学习应用

神经网络

• 起源
• 基本结构

神奇的分类能力以及背后的原理

• 感知器与逻辑门
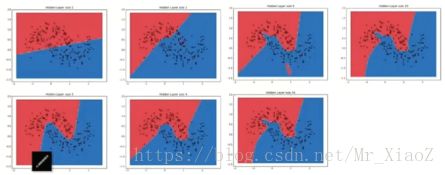
• 强大的空间非线性切分能力
• 网络表达力与过拟合问题
• BP算法与SGD

代码与示例

• Tensorflow多层感知器非线性切分
• 神经网络分类（非线性）示例
• CIFAR-10多层感知器切分

---

深度学习与应用

图像上的应用 12年之前是分水岭，之后使用了CNN。

NLP上的应用 模仿出来作家的文笔 RNN写代码 LSTM

综合应用

一点基础：线性分类器

1、线性分类器得分函数 

CIFAR-10：一共有10个类别，几千张图片的分类任务

给你一张图片，然后得出每个类别的分数是多少，结果是一个得分向量score-vector

我们把[32,32,3]的图片看成x，线性分类器就是给出权重W，得到10个得分

简单一点，我们把32*32*3的矩阵拉成一个3072*1的向量，最后我们想得到10维的得分向量，那么我们的权重W就得是10*3072的矩阵，相乘后得到10*1的向量

f是一个函数，它所做的事情非常简单，就是就输入矩阵映射成为得分向量，决定这个得分函数的就是W，我们希望得到最合适的一组W。

 

识别图像---其实就是分类问题

3：RGB

给你一张图片，也就是一个矩阵，让你完成一个任务，识别图像中的内容找出分类，一共有10个类别几千张图片

把你输入的矩阵x，通过f，映射为一个得分向量

把图像做一个reshape，将其拉成一个一维3072*1的向量。

为了得到一个10*1的矩阵（向量），要配给W一个10*3072，所以10*3072 与 3072*1 相乘，得到一个10*1的列向量，就认为是一个10维的得分向量

实例：

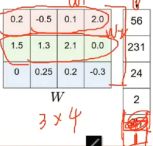
我们输入一个图像，拉伸后成为1维，为了方便，简单为4*1的向量，得分向量为3个分类，3*1,于是我们的W就要是一个3*4的矩阵，线性分类器嘛，有偏置项b(wile增加灵活性)，最后我们得到y=W*x+b的线性函数（得分函数,y就是得分向量）。

上面的W在dog类别中得分最高，这显然不是我们想要的，我们想要的是在正确的类别上有较高的得分，在错误的类别得分较低，所以我们要做的是修正这个W，使我们输入一张图片后，在正确的类别上得分最高

。

2、线性分类器的理解---空间划分

Wx+b是空间的点

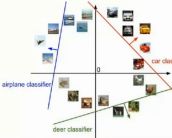
上面的例子中，有3个类别，我们可以把W的第一行+b看做是决定第一个类别的最终得分，W的第二行+b决定第二个类别的分数，以此类推，我们三个不同的W和b其实就是对于空间中进行了划分，相当于三个直线（确切说是超平面，）然后我们输入不同的x，其实就是空间中的不同区域。

线性分类器的理解---模板匹配（模板指的是W中的某一行）

W的每一行可以看做是其中一个类别的模板

每类得分，实际上是像素点和模板匹配度

模板匹配的方式是内积运算

没有b的情况：

注意哈：有些写成了y=wx，没有偏置项b，可能是这样处理的---将偏置项的值装到了W矩阵的最后一列，然后在x向量中增加一个1，也就是：

3、损失函数 LossFunction/CostFunction--衡量吻合程度

给定W，可以由像素映射到类目得分

可以调节参数（权重）W，使得映射的结果和实际类别吻合

损失函数是用来衡量吻合程度的。

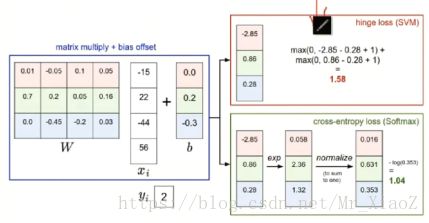
损失函数1：hinge loss支持向量机SVM损失

给你一套试卷，要求你在正确题目的得分要比其他任何错误题目的得分要高出来一个值Δ，你要是所有的都高出了Δ，好，不动，要是没有高出，那就加一个惩罚值（你缺的多少就惩罚多少）

具体：

对于训练集上第i张图片数据xi

在W下会有一个得分结果向量f（xi,W）

第j类的得分为f（xi,W）j

则在该样本上损失我们由下列公式计算得到

：其余类别上的得分

：正确类别上的得分

现在我们由三个类别，而得分函数计算某张图片的得分为f（xi,W）= [13,-7,11],而实际的结果是第一类yi=0,假设Δ=10（在正确的类别上的得分比错误上的类别高出至少10分），上面的公式把错误类别(j不等于yi)都遍历一遍，求值加和：

 

损失函数2：cross-entropy（交叉熵）softMax

做一个归一化，在A、B、C、D四个选项中选择他们的概率有多高，我自己有一份标准答案（概率向量），评估你得到的概率和我的标准答案（概率）之间的距离

对于训练集中的第i张图片数据xi

在W下会有一个得分结果向量fyi

则损失函数记做：

 或者

实际工程中计算的方法是

因为e的指数次方是得分，如果太高的话容易溢出

其实softmax损失就是将之前的得分换成了概率。

2种损失函数的理解:

注意哈：这都是属于线性分类器的损失函数

矩阵相乘W*x+b得到了得分向量，然后我们首先是hingeloss（SVM），就是算正确类别的得分要比错误类别的得分高出一个Δ，然后高了没问题，没高就补充缺少的分数，交叉熵损失就是将得分向量转化为了概率（转换公式），然后做一个归一化，我自己有一个标准答案，然后评估你的概率和标准答案之间的距离

求两个之间的最小值，可以用梯度下降，牛顿法

神经网络

神经网络是什么？

通用的学习框架

Speech recognition

Handwritten recognition

Playing go

Dialogue system

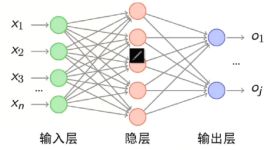
·神经网络结构大概如下

从神经网络到感知器

感知器：

图中的b和w1,w2有错误，表达为下图

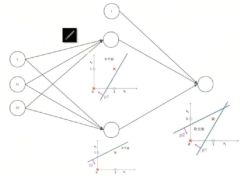
添加少量隐层---浅层神经网络

 

增多中间隐藏层---深度神经网络

 

神经网络之为什么？

神经网络应用在分类问题中效果好

LR或者Linear SVM用于线性分割，但是非线性如何处理? 为何不用他们？

 

非线性可分，怎么办？

 

神经元完成【逻辑与】

 

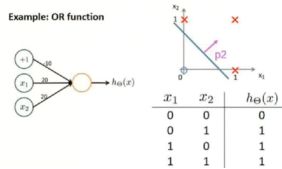
神经元完成【逻辑或】

对线性分类器的【与】和【或】的组合--完美对平面样本点分布进行分类

神经网络表达力和过拟合

1. 理论上说单隐层神经网络可以逼近任何连续函数，只要隐层的神经元的个数足够多
2. 虽然从数学上看表达能力一致，但是多隐层的神经网络比单隐层的神经网络工程效果要好很多
3. 对于一些分类数据（如CTR预估），3层神经网络效果优于2层神经网络，但是如果把层数不断增加(4/5/6)层，对最后结果的帮助就没有那么大的跳变了
4. 图像数据比较特殊，是一种深层（多层次）的结构化数据，深层次的卷积神经网络，能够更充分和准确地把这些层级信息表达出来。
5. 提升隐层层数或者隐层神经元的个数，神经网络“容量”会变大，空间表达力会变强。

• 过多的隐层和神经元节点，会带来过拟合问题。
• 不要试图通过降低神经元网格参数量来减缓过拟合，用正则化或者dropout

 

神经网络之传递函数（激活函数）

详见激活函数文章

激活函数作用：对于你输入的x做一个非线性的变换

·理解1：对信号做一个过滤，以决定我们让不让信号过去以及以多大的程度过去

你在路边打电话，突然吹来了一阵风，但是你并不会因此而停下来你打电话的动作，如果有人突然打了你一拳，你会立即停止打电话。上面说明前者的信号并不是有用，你需要将它的信号压缩为0，后者信号有用，可以将信号变成1。

·理解2：如果没有非线性的变换，我们叠加更多的线性变换，并不能实现非线性的变换，累加不同的layer只是改变前面的系数，而这个系数我们在单层的时候也可以学得过来。所以累加多少层都没有用，如果我们不在中间假如非线性的变换。

 

神经网络之BP算法

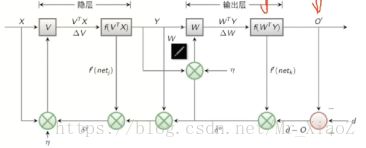
·正向传播求损失，反向传播回传误差

·根据误差信号修正每层的权重。

首先我们以三层为例

输入层输入x1,x2...xn经过1个隐藏层最后输出层输出o1,...oj

我们得到的输出结果o1,...oj再和标准答案进行比较d1,...dn

我们的损失函数E就用最小二乘法的进行表示

我们的目的就是使得下图中的E尽可能地小

首先是，然后其中的ok是由靠近输出层的隐层传递而来的，每一层都是一个传递函数（激活函数），所以ok=f(net k)=f(),别忘了其中的yj是倒数第二层的传递而来的，所以又是一层复合，最后展开至输入层

 

神经网络之SGD --- 一阶的方法

我们一般都是使用mini-batch SGD，因为单个样本的稳定性不够，震荡地太厉害了。

 

误差E有了，怎么调整权重让误差不断减小？

E是权重w的函数，我们需要找到使得函数值最小的w

 

 

BP算法实例

我们的输出是0.01和0.99，我们的输入是0.05和0.10，我们希望可以找到一组合适的w和b，来实现我们的输出目的。

我们最开始并不知道我们的w和b到底是什么，所以我们随手敲了一组数，0.15,0.20,0.25,0.30和b=0.35以及后面的0.40...，然后开始做修正了。

 

修正开始之前我需要先前向传播看一下我这个参数w和b做出来的结果和标准的结果之间的差距，所以开始一层层地计算

前向传播之后得到了结果o1和o2，发现差距很大啊

然后我们开始计算E，loss，注意哈，中间的传递函数是sigmoid函数

然后我知道自己的结果和正确的结果差距很大，于是便开始弥补差距

 

下图为修正w5：

算出来E对于w5的偏导之后我们就可以使用SGD进行修正

w6-8同理可得。