论文笔记:Large Scale GAN Training for High Fidelity Natural Image Synthesis
进入正题之前,UP主想要吐槽一下,关于这篇文章的很多博客好多人都是直接记录了前面的部分;
即作者介绍的5个tricks用于高清图像256×256甚至是512×512,然后给了一堆结果。
就完了,。那后面的讨论分析呢??
本着一探究竟的蛮劲,UP主特意花了一天的时间去读了这篇博客(这里倒是挺好奇,其他道友读论文的花费时长的●_●)
进入主题,下面我们根据文章的组织路线来解读这篇文章。
Introduction
首先是,GAN的训练是动态的,并且几乎对所有的实验设置都很敏感(有优化器参数(lr, momentum)等到模型的结构)。
其次是,GAN用于图像合成(传统的基于Noise决定的基本语义(如姿态、角度),与基于Class的样式(如类别、纹理),两个latent vecotr/embedding)的“向量→图像”的合成方式),存在保真度(fidelity)与多样性(variety)的矛盾(即GAN需要在二者之间找到一个平衡)。
Contribution
1. 证明了GANGAN的性能极大地受益于模型的放大(scale)(如每层的channels数增加,batch size增大,输入图像的resolution增大等)
当然,这之间会出现一些问题,作者也讨论了这些问题该如何解决。
2. 引入了一个简单的noise的采样技巧来权衡生成器生成样本的fidelity与variety。
3. 讨论了针对large scale GAN的训练不稳定性(instability),提出,基于现在的技术,我们能够降低这些不稳定性,但这回伴随着巨大的模型性能的降低(如生成模型变差了,体现为IS分数降低或者FID分数增大)。
Background
首先我们简要回顾下传功的图像合成GAN,基于下面的目标函数——
min G max D E x ∼ p d a t a ( x ) [ log D ( x ) ] + E z ∼ p ( z ) [ log ( 1 − D ( G ( z ) ) ] \mathop{\min}\limits_{G} \mathop{\max}\limits_{D} \mathop{\Bbb E} _{x \thicksim p_{data}(x)}[\mathop{\log}D(x)] + \Bbb{E}_{z \thicksim p(z)} [\log (1-D(G(z))] GminDmaxEx∼pdata(x)[logD(x)]+Ez∼p(z)[log(1−D(G(z))]
其中,z 是一个潜在的变量,从一个随机分布 p(z) 中采样得到,如正态分布 N(0, I) 或者均匀分布 U[-1, +1]。
现在生成模型GAN的工作主要有三个方面:
1)修改目标函数(objective function);
2)对D增加梯度惩罚(Gradient Penalty);
3)另外就是从模型结构的选择角度去看(本文的基本结构是SA-GAN(Self-attention GAN)).
** 这里放一张图,读者们应该很快就可以get到这是什么简单但NB的东西了。
这里附赠链接:SA-GAN.
另外,这里介绍一下conditional GAN的一些基本知识。
最开始的做法是:将class类别信息以“one-hot”向量形式与noise向量拼接在一起作为输入,并在目标函数中加入一个分类器模块,这是多么朴素的思想;
后来出现了,将class或者style的信息经过MLP变换后,得到normalization(如IN,BN等)的参数(scaling factor: γ,与bias factor: β);这主要是基于白化与着色的思想(通过μ与σ可以实现两个数据分布之间的相互转换)。
Scale Up the GAN
这一部分主要讲解了如何通过“放大”GAN来实现不同分辨率的图像合成质量,得到更好地生成模型(基于ImageNet)。
| 首先我们介绍一些实验的配置 |
|---|
| 以SA-GAN作为baseline |
| 对抗loss使用Hinge Loss |
| 将class info 作为BN的参数引入 |
| 对G使用Spectral Norm 谱正则化 |
| 模型使用Orthogonal Initialization或者Xavier Initialization |
| 生成器G使用moving averages of weights的方式,其中,decay=0.9999 |
下面我们介绍一下作者使用的5个tricks及其对应的效果。
1. Simply increase the batch size;
** 比较下图1、2、3、4行
2. 增加每一层的宽度(# of channels) by 50%,即为原来的1.5倍;
** 比较4、5行
3. 共享class information的embedding(换句话说,就是每一层的BN的参数都来自于同一个class embedding的变换结果,可以是只做一次变换,也可以对应每层做一次变换);
**比较5、6行
4. noise不单单是在第一层输入,也在多层输入
(有利于不同分辨率下的特征对noise信息的直接利用)
** 比较6、7行
5. 正交正则项(下面会介绍)
** 比较7、8行
(第8行是论文的方法)
下面主要是进行一个讨论
1)关于noise的latent space的讨论
作者首先介绍了一些常用的采样的数据分布
| Data Distribution | Notes |
|---|---|
| N ( 0 , I ) \mathcal {N}(0, I) N(0,I) | 标准的latent space |
| U [ − 1 , 1 ] \mathcal {U} [-1, 1] U[−1,1] | 另一个标准的latent space |
| B e r n o u l i { 0 , 1 } Bernouli \{0, 1\} Bernouli{0,1} | 离散的隐向量,这是基于先验“自然界的图像并不是连续的,而是离散的(one feature is either present or not),即latent vector某个元素的值要么是1要么是0” ,实验证明这个的效果要比使用正态分布的效果好 |
当然还有其他的,这里就不列举了。
作者提出了Truncation Trick,具体做法是:
## truncating a 'z' vector by resampling(重采样) the values with magnitude(模长) above a chosen threshold leads to improvement in individual sample quality at the cost of reduction in overall sample variety.
显然,由于G需要映射的范围被缩小了,所以对于单张图像的合成效果更好;
但由于源域的空间缩小,也使得总体的生成图像多样性受损。
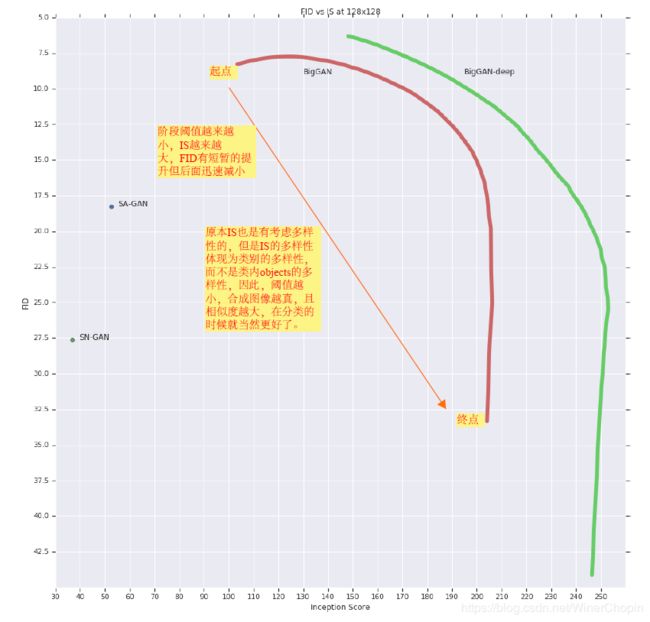
我们看一下下面的例子:(从左到右,选择的阈值分别是:2, 1, 0.5, 0.04)
我们还可以进一步分析:
IS分数计算的是分布 p(y|x) 与 p(y) 之间的KL散度,
前者表示分类的准确性(我们希望它是一个脉冲函数,这样说明生成的图像更像对应某个类别的图像),
后者表示含有多少类(应该是一个uniform的分布,因为我们希望合成图像足够多样化)。
但是,当我们使用Truncation Trick的时候,一方面G的性能提高合成图像更加自然,
同时尽管总体多样性减少了,但是只要保证所有类别都可以被差不多平均地顾及到,
至于类内部的图像多样性如何并不影响 p(y) 的分布。
因此 ,Truncation Trick能够提高IS分数。
至于FID,其原理是考察a set of generated data之间的均值与方差,“多样性”是针对sample而言的(相比于IS是针对class而言的),因此,FID势必直接受到削弱。
综上,我们可以得到下面的图:
但是,作者发现这个方法并不是总是行得通;上述的规律对于许多大的模型是不被服从的,相反会产生artifacts,如下图:
我们可以反思:是不是如下面的artifacts在源域<<目标域的时候就会出现?
为了解决上面的问题,作者认为,这是因为基于大小的“超球”范围内的限制使得模型G不够平滑
(我们设想一下:原先我们已经针对本次input准备好了reference(包括class info),但是这时候你使用Truncation认为地把input调换了(就好像是一次反射取值),那么得到的映射内部是绕来绕去的)
所以我们需要去平滑一下它。
于是作者提出了Orthogonal Regularization去解决它。
基本出发点是对网络权重做简化。
R β ( W ) = β ∣ ∣ W T W − I ∣ ∣ F 2 R_{\beta}(W)=\beta||W^TW-I||_{F}^2 Rβ(W)=β∣∣WTW−I∣∣F2
其中的 F-范数是矩阵内所有元素的平方和开根号。
但是这个限制太强了,他直接要求矩阵对角线元素必须接近于1,然后其他元素接近于0.
作者提出了个改良版本:
R β ( W ) = β ∣ ∣ W T W ⊙ ( 1 − I ) ∣ ∣ F 2 R_{\beta}(W)=\beta||W^TW \odot (1-I)||_{F}^2 Rβ(W)=β∣∣WTW⊙(1−I)∣∣F2
我们可以看到,这么一来就取消了对矩阵主对角线元素的限制。
总结一下这一部分:
我们证明了凭借目前的技术,通过“放大”GAN能够实现生成模型性能的提高;
但是我们的大模型在训练的时候遭遇了“training collapse”,因此我们需要在崩溃发生之前停止训练,或者仅仅使用崩溃前的checkpoints的模型用于测试。
下面我们会讨论一下,为什么同样的用于之前的小模型的设置,用于大模型的时候就会出现崩溃?
Analysis of Training Collapse for Large Models
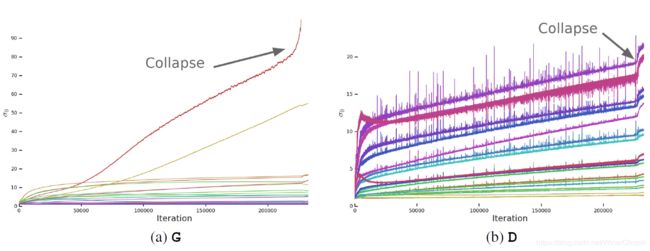
我们通过监视:range of weight, gradient, and loss statics来观察崩溃发生时模型发生了什么。
上图展示了,训练过程中,G/D的每一层卷积的权重W的第一个奇异值(σ0)的大小。
初步观察我们可以发现:
对于G,崩溃发生时,大部分的层都保持着well-behaved spectral norms;只有少数层尤其是G的第一层是ill-behaved的。并且表现为“explode at collapse”(爆炸性增长)。
对于D,我们发生正常训练的过程中,每一层的spectral norms是相对noiser的。崩溃发生时,数不分层出现了spectral norms值的跳跃(跃迁),而不是像G那样增长。
我们希望知道,G和D的这两种表现是不是就是大型GAN训练不稳定的充要条件。
对于G,我们通过下面的实验:
直接限制spectral norm的爆炸性增长,看看这样collapse是否还会发生首先我们知道,对矩阵作奇异值分解(SVD),奇异值是按照从大到小排列的,即有:
σ 0 > > σ 1 > > σ 2 > > . . . \sigma_0 >> \sigma_1 >> \sigma_2 >> ... σ0>>σ1>>σ2>>...
所以我们只要限制 σ 0 \sigma_0 σ0 的大小即可。具体按如下操作:
- 设置某个阈值 σ c l a m p \sigma_{clamp} σclamp (当 σ 0 \sigma_0 σ0 的值超过它的时候,我们就对它做截断);
所以条件当然是下面的形式:
max ( 0 , σ 0 − σ c l a m p ) \max (0, \sigma_{0}-\sigma_{clamp}) max(0,σ0−σclamp)- 这个阈值可以这么设:
① 取一个固定的值 σ r e g \sigma_{reg} σreg ;
② 取第二奇异值的某个倍数 r × s g ( σ 1 ) r \times sg(\sigma_1) r×sg(σ1) ,其中的 s g sg sg 具体是什么我也不大清楚,,- 具体如何操作于 W W W 才能作用到 σ 0 \sigma_0 σ0 呢?
我们联系SVD的过程:
W = U Σ V T W=U\Sigma V^T W=UΣVT
然后考虑到 Σ \Sigma Σ 是一个对角矩阵,这说明, U Σ U\Sigma UΣ 的操作实际上是对应每个奇异值 σ i \sigma_i σi 对矩阵 U U U 的第 i i i 列作scaling。
那么,如果只考虑 σ 0 \sigma_0 σ0 的话,上述操作可以等价于: σ 0 u 0 v 0 ∈ R m × n \sigma_0u_0v_0 \in \R^{m\times n} σ0u0v0∈Rm×n;
其中 u 0 u_0 u0 和 v 0 v_0 v0 分别表示矩阵 U U U 和 V V V 的第一奇异向量(singular vectors)。
考虑到矩阵点乘的叠加性,就有:
W = W − max ( 0 , σ 0 − σ c l a m p ) . u 0 v 0 W=W-\max (0, \sigma_0-\sigma_{clamp}) . u_0v_0 W=W−max(0,σ0−σclamp).u0v0
但实验结果是——
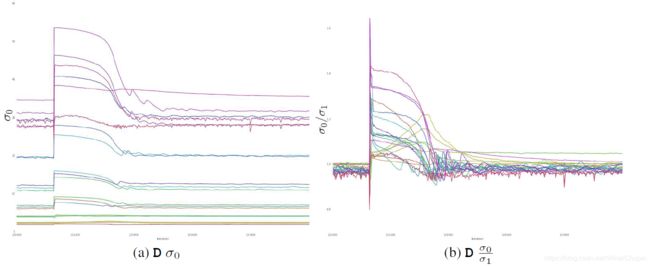
不管加不加Spectral Norm,这样的限制确实阻止了 σ 0 \sigma_0 σ0 或者 σ 0 σ 1 {\sigma_0}\over{\sigma_1} σ1σ0 的逐渐增长或者爆炸,但还是无法阻止崩溃的发生。
结论:即使赋予了G更多的限制条件,仍然不够充分保证训练的一致性。
既然从G下手无法阻止崩溃,我们转而研究D。
我们假设:
产生振荡的原因是它定期收到了较大的梯度
我们可以更仔细地看每一个振荡,如下图
我们有理由猜测:这是与当下GAN的训练方式有关:d D-steps per single G-step
每次G让D对fake data的响应值取反(原本D是希望 D ( x f a k e = 0.0 D(x_{fake}=0.0 D(xfake=0.0 ),这时候梯度会突变(因为更新的方向可以说是相反了)对D造成了扰乱;但随着后面的几个 D-steps ,D的梯度慢慢稳定下来。
因此一个自然的想法就是对D的梯度做惩罚(Gradient Penalty)
在D的目标函数中加入GP正则项:
R 1 : = γ 2 E p D ( x ) [ ∣ ∣ ∇ D ( x ) ∣ ∣ F 2 ] R_1:={{\gamma}\over2}\Bbb E_{p_{\mathcal D}(x)}[||\nabla D(x)||_F^2] R1:=2γEpD(x)[∣∣∇D(x)∣∣F2]
我们建议让 γ = 10 \gamma=10 γ=10
实验结果
- 确实训练变得稳定,并且提高了D的各层 W W W 的 σ 0 \sigma_0 σ0 的曲线的平滑度;
- 但是模型的性能严重下降(performances severely degrades)(IS分数降低了约45%);
- 发现降低 γ \gamma γ 可以减缓性能的下降,但是慢慢地会出现 ill-behaved spectra(即使使用最小的 γ \gamma γ 可以保证训练稳定,IS还是降低了20%)。
结论:对D的梯度惩罚力度加大,训练稳定性能够被实现,但换来的是模型性能的下降。
上面是从weights的角度去看,下面我们试着从loss去看。
我们还发现,D的loss在训练过程中趋近于0
Hinge Loss的计算如下:
L D H i n g e G A N = E x r ∼ P [ max ( 0 , 1 − D ( x r ) ) ] + E x f ∼ Q [ max ( 0 , 1 + D ( x f ) ) ] L_{D}^{HingeGAN}=\Bbb E_{x_r \sim \Bbb P}[\max(0, 1-D(x_r))]+\Bbb E_{x_f \sim \Bbb Q}[\max(0, 1+D(x_f))] LDHingeGAN=Exr∼P[max(0,1−D(xr))]+Exf∼Q[max(0,1+D(xf))]
L G H i n g e G A N = − E x f ∼ Q [ D ( x f ) ] L_G^{HingeGAN}=-\Bbb E_{x_f\sim \Bbb Q}[D(x_f)] LGHingeGAN=−Exf∼Q[D(xf)]
当鉴别器 D D D 足够优秀的时候,对real data输出为1,对fake data输出为-1,那么loss就是0.0了。
当崩溃发生的时候,loss会产生骤然的跳跃。
因此我们猜测:会不会是D过拟合了?
于是,鉴于鉴别器D本身是一个二分类器,我们将崩溃前训练好的D拿出来,对训练数据和测试数据分别作real与fake的二分类,结果是:在训练数据上准确率是98%,但是到了验证集上就只有50%-55%了,这就好比随机猜测。
显然D过拟合了,记住了训练数据集,那这对于G没有影响,因为此时D是optimal的,能够总是为G产生有用的梯度引导。
总结一下这一部分:
我们发现训练的不稳定性不仅仅与G、D有关,还与他们之间的对抗训练的过程有关。
基于目前的技术,我们可以通过限制D来保证训练的稳定性,但是会导致模型G性能的严重下降。
因此,沃恩只能够允许崩溃的存在,并且在崩溃之前尽可能保存最优的模型。
到这里,我们自然而然会产生一个问题(Appendix G):
既然崩溃无法阻止,那是否可以延迟它?
或者是在快要崩溃的时候保存模型,然后修改参数后再继续训练?
我们发现:
1)修改学习率
① 增大学习率 lr ,不管是在G还是D还是两者都,都会导致崩溃;
② 保持 l r D lr_D lrD 不变,只减小 l r G lr_G lrG,可以延迟崩溃(有时候可以延迟100 000个iterations),但这会稍微破坏了训练——模型的性能要么不变要么稍微下降;
③ 减小 l r D lr_D lrD ,保持 l r G lr_G lrG 不变,导致崩溃。
** 我们认为,当 l r D lr_D lrD 减小后,会使得 D 的更新跟不上 G,所以才导致的崩溃,所以我们追加了实验: l r D ↓ lr_D \downarrow lrD↓, l r G lr_G lrG 不变,但是 d D s t e p s / G s t e p ↑ d ~D_{steps}/G_{step} \uparrow d Dsteps/Gstep↑,结果也是要么无效,要么可以延迟崩溃但是以些许的性能下降作为代价。
2)冻结模型
① 在崩溃发生前冻结G,看看D是否可以稳定→ D保持稳定,并且loss逐渐趋向于0;
② 在崩溃发生前冻结D,看看G是否保持稳定→ G迅速崩溃,将D的loss带动到300,相较于正常情况下都是0~3.0之间。
结论:
1)D必须始终保持最优,这是由
min G { max D V ( G , D ) } \mathop{\min}\limits_{G} \{\mathop{\max}\limits_{D}V(G,D)\} Gmin{DmaxV(G,D)}
决定的;
2)训练过程中要偏袒D(可以是增大D的学习率,增加D的迭代次数等),仍旧不足以充分保证训练的稳定性,这有两种可能性:
① D保持了最优,但这对于稳定训练本身是必要但不充分的;
② 训练过程中出于某些技术上的限制,D始终未达到最优。
上面的training instabilities/collapse for large GAN的讨论终于结束啦!!
Results
首先是比较简单的例子
然后是更多例子
再者是一些插值的例子:对z或者c进行插值。
上面↑是对z和c同时插值的结果;下面↓是只对c做差值、z保持不变的结果。
我们可以发现:
z z z 表征的是语义、姿态;
c c c 表征的是具体的类别与细节、纹理、颜色等。
最后则是一个非常有趣但是周到的实验:
前面我们不是证明了D在训练过程中过拟合了吗?那么,会不会G也过拟合了?
于是作者做了下面的实验:
对训练好的G合成的图像,经过在image-level或者feature-level(由某些预训练好的模型)去原来的训练集中寻找最近邻。
如果找到的图像是极其相似的,说明我们的G也过拟合了;否则则没有过拟合,G可信。
下图是使用VGG-16的fc7层输出进行匹配的↓
下图是根据pixel匹配的↓
下图是根据ResNet-50 avgpooling输出匹配的↓
结论:G没有过拟合,G可信!
结束语
好吧,为了彻底弄懂这篇文章,尤其是GAN的内部,我整整画了1,5天的时间,这也是近来花时间最多的一篇论文了,CAI is the original sin ٩(●̮̃•)۶!
UP主去面壁了!