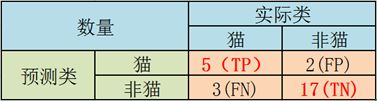
弄清楚机器学习中的评价指标：混淆矩阵、Acuracy、Precision、Recall、F1-Score、ROC、AUC

一、混淆矩阵

在机器学习领域，特别是统计分类问题，混淆矩阵，也称为误差矩阵，是一种特定的表格布局，允许可视化算法的性能，通常是监督学习的算法（在无监督学习通常称为匹配矩阵）。 矩阵的每一行代表预测类中的实例，而每列代表实际类中的实例（反之亦然,Tensorflow和scikit-learn采用另一方式表示）。“混淆”一词源于这样一个事实：它可以很容易地看出系统是否混淆了两个类（即通常将一个类错误标记为另一个类）。
它是一种特殊的列联表(contingency table)，具有两个维度（“实际”和“预测”），以及两个维度中相同的“类”集（维度和类的每个组合都是列联表中的变量）。
混淆矩阵是除了ROC曲线和AUC之外的另一个判断分类好坏程度的方法。

以下有几个概念需要先说明：
预测值为1，记为P（Positive）
预测值为0，记为N（Negative）
预测值与真实值相同，记为T（True）
预测值与真实值相反，记为F（False）

TP	True Positive	真阳	真实为1，预测也为1
FN	False Negative	假阴	真实为1，预测为0
FP	False Positive	假阳	真实为0，预测为1
TN	True Negative	真阴	真实为0，预测也为0

举个例子：
如果分类系统已经过训练以区分猫，狗和兔子，则混淆矩阵将总结测试算法的结果以供进一步检查。假设有27只动物的样本：8只猫，6只狗和13只兔子，产生的混淆矩阵如下表所示：

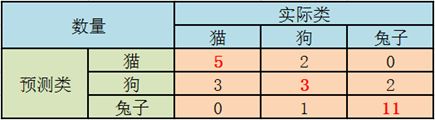
在这个混淆矩阵中，在8只实际的猫中，系统预测三只是狗，而在六只狗中，它预测一只是一只兔子，两只是猫。 我们可以从矩阵中看出，所讨论的系统难以区分猫和狗，但可以很好地区分兔子和其他类型的动物。 所有正确的预测都位于表格的对角线上（以粗体突出显示），因此很容易在视觉上检查表格中的预测错误，因为它们将由对角线外的值表示。

混淆表

在预测分析中，混淆表（有时也称为混淆矩阵）是具有两行和两列的表，其报告假阳性，假阴性，真阳性和真阴性的数量。这允许更详细的分析，而不仅仅是正确分类的比例（准确性）。准确性不是分类器实际性能的可靠度量，因为如果数据集不平衡（即，当不同类别中的观察数量变化很大时），它将产生误导性结果。例如，如果数据中有95只猫和只有5只狗，一个特定分类器可能将所有观察结果归类为猫。总体准确度为95％，但更详细的分类器对猫类的识别率（灵敏度）为100％，而狗类的识别率为0％。在这种情况下，F1-score甚至更不可靠，并且这将产生超过97.4％=2*0.95%*100%/(95%+100%)。

混淆矩阵的缺点：

一些positive事件发生概率极小的不平衡数据集(imbalanced data)，不平衡数据集也就是正负样本的比例相差很大，混淆矩阵可能效果不好。比如对信用卡交易是否异常做分类的情形，很可能1万笔交易中只有1笔交易是异常的。一个将所有交易都判定为正常的分类器，准确率是99.99%。这个数字虽然很高，但是没有任何现实意义，因为错检率也是100%。

假设上面的混淆矩阵，对于cat类，其相应的混淆表将是：

混淆矩阵的指标
预测性分类模型，肯定是希望越准越好。那么，对应到混淆矩阵中，那肯定是希望TP与TN的数量大，而FP与FN的数量小。所以当我们得到了模型的混淆矩阵后，就需要去看有多少观测值在第二、四象限对应的位置，这里的数值越多越好；反之，在第一、三四象限对应位置出现的观测值肯定是越少越好。

混淆矩阵延伸出的各个评价指标
但是，混淆矩阵里面统计的是个数，有时候面对大量的数据，光凭算个数，很难衡量模型的优劣。因此混淆矩阵在基本的统计结果上又延伸了如下4个指标：

准确率（Accuracy）：针对整个模型(包括了所有class的总体准确率)
精确率（Precision）
召回率（Recall）：就是灵敏度（Sensitivity）
F1-Score:也被称为F1-measure

二、Acuracy

Accuracy = (TP+TN)/(TP+FP+TN+FN)
预测对的数量对总的预测数量的占比。

三、Precision

precision=TP/(TP+FP)
真阳对预测为阳的占比。

四、Recall

recall=TP/(TP+FN)
真阳对真实为阳的占比。

五、F1-Score

F1-Score又称为平衡F分数（balanced F Score），他被定义为精准率和召回率的调和平均数。

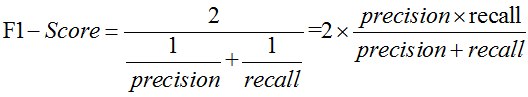
F1-Score指标综合了Precision与Recall的产出的结果。F1-Score的取值范围从0到1的，1代表模型的输出最好，0代表模型的输出结果最差。
更一般的，我们定义Fβ分数为

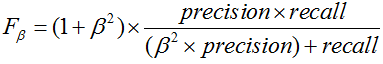
除了F1分数之外，F2分数和F0.5分数在统计学中也得到大量的应用。其中，F2分数中，召回率的权重高于精准率，而F0.5分数中，精准率的权重高于召回率。

六、F1-Score的意义是什么？

人们通常使用精准率和召回率这两个指标，来评价二分类模型的分析效果。但是当这两个指标发生冲突时，我们很难在模型之间进行比较。比如，我们有如下两个模型A、B，A模型的召回率高于B模型，但是B模型的精准率高于A模型，A和B这两个模型的综合性能，哪一个更优呢？

Rate	精准率	召回率
A	80%	60%
B	70%	90%

F1-Score(A) = 68.57, F1-Score(B)=78.75,显然B模型更优。

再看另一例

Rate	精准率	召回率
A	80%	90%
B	90%	80%

算出的F1-Score(A)=F1-Score(B),就不太好判断了。为了解决这个问题，人们提出了 Fβ分数。Fβ的物理意义就是将精准率和召回率这两个分值合并为一个分值，在合并的过程中，召回率的权重是精准率的β倍 [1] 。F1分数认为召回率和精准率同等重要，F2分数认为召回率的重要程度是精准率的2倍，而F0.5分数认为召回率的重要程度是准确率的一半。

举例：要对产品分类：正品和次品。现在有200个产品，刚好100个正品，100个次品，训练之后的预测50个正品，150个次品，即：预测50个正品正确，有50个正品被预测为次品，100个次品预测全部正确。
此时：
TP: 50
FP: 50
FN: 0
TN: 100
TPR: 0.5
FPR: 0.5
Accuracy: 75%
Precision: 100%
Recall: 50%
F1-Measure: 66.7% 即(2323)

另外补充一些经常用到的评价指标。

假阳率：假阳对本来为阴的占比。

七、ROC

ROC全称是“受试者工作特征”（Receiver Operating Characteristic）。ROC曲线的面积就是AUC（Area Under the Curve）。AUC用于衡量“二分类问题”机器学习算法性能（泛化能力）。
截断点：机器学习算法对测试样本进行预测后，可以输出各测试样本对某个类别的相似度概率。比如t1是P类别的概率为0.3，一般我们认为概率低于0.5，t1就属于类别N。这里的0.5，就是”截断点”。
总结一下，对于计算ROC，最重要的三个概念就是TPR, FPR, 截断点。
截断点取不同的值，TPR和FPR的计算结果也不同。将截断点不同取值下对应的TPR和FPR结果画于二维坐标系中得到的曲线，就是ROC曲线。横轴用FPR表示。
先看一段python代码：

#-*-coding=utf-8 -*-

'''
import numpy as np
import copy
import sklearn.metrics as metrics
import matplotlib.pyplot as plt

'''
labels表示标签，0表示负例，1表示阳例，对应的score表示预测为阳例的得分
'''
labels = [0,        0,      1,      1]
scores = [0.1,    0.4,   0.35,    0.8]

fpr, tpr, thresholds = metrics.roc_curve(labels, scores, pos_label=1)
print("fpr:"+str(fpr))
print("tpr:"+str(tpr))
print("thresholds:"+str(thresholds))
roc_auc = metrics.auc(fpr, tpr)
print("ROC_AUC:%0.2f"%(roc_auc))
plt.plot(fpr, tpr, label='ROC (area = %0.2f)' % (roc_auc))
plt.show()

运行结果如下：

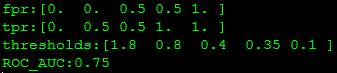
将结果中的FPR与TPR画到二维坐标中，得到的ROC曲线如下（蓝色线条表示），ROC曲线的面积用AUC表示（黄色部分）。

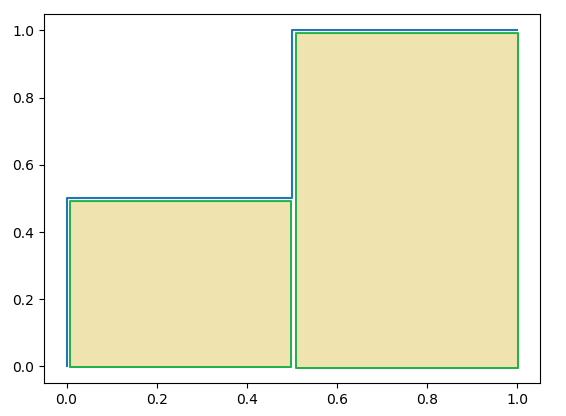
详细计算过程

上例给出的数据如下：

labels = [0,        0,      1,      1]
scores = [0.1,    0.4,   0.35,    0.8]

用这个数据，计算TPR，FPR的过程是怎么样的呢？

1、分析数据

labels是一个一维数组（样本的真实分类）。数组值表示类别（一共有两类，0和1）。我们假设labels中的0表示反例(N)，1表示正例（P）。score即各个样本属于正例的概率。

2. 针对score，将数据排序

样本	预测属于正例的概率(score)	真实类别
y[0]	0.1	N
y[2]	0.35	P
y[1]	0.4	N
y[3]	0.8	P

3. 将截断点依次取为score值

将截断点依次取值为0.1,0.35,0.4,0.8时，计算TPR和FPR的结果。

3.1 截断点为0.1

说明只要score>=0.1，它的预测类别就是正例。
此时，因为4个样本的score都大于等于0.1，所以，所有样本的预测类别都为P。

scores = [0.1, 0.4, 0.35, 0.8]
label_true = [0, 0, 1, 1] 
lable_pred = [1, 1, 1, 1]

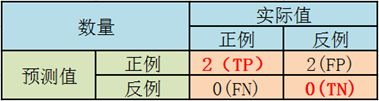
TPR = TP/(TP+FN) = 1
FPR = FP/(TN+FP) = 1

3.2 截断点为0.35

说明只要score>=0.35，它的预测类别就是P。
此时，因为4个样本的score有3个大于等于0.35。所以，所有样本的预测类有3个为P（2个预测正确，1一个预测错误）；1个样本被预测为N（预测正确）。

scores = [0.1, 0.4, 0.35, 0.8]
label_true = [0, 0, 1, 1] 
label_pred = [0, 1, 1, 1]

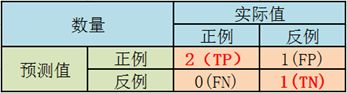
TPR = TP/(TP+FN) = 1
FPR = FP/(TN+FP) = 0.5

3.3 截断点为0.4

说明只要score>=0.4，它的预测类别就是P。
此时，因为4个样本的score有2个大于等于0.4。所以，所有样本的预测类有2个为P（1个预测正确，1一个预测错误）；2个样本被预测为N（1个预测正确，1一个预测错误）。

scores = [0.1, 0.4, 0.35, 0.8]
label_true = [0, 0, 1, 1] 
label_pred = [0, 1, 0, 1]

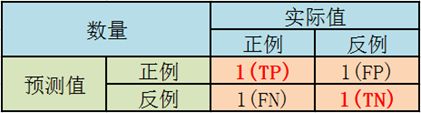
TPR = TP/(TP+FN) = 0.5
FPR = FP/(TN+FP) = 0.5

3.4 截断点为0.8

说明只要score>=0.8，它的预测类别就是P。所以，所有样本的预测类有1个为P（1个预测正确）；3个样本被预测为N（2个预测正确，1一个预测错误）。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1] 
y_pred = [0, 0, 0, 1]

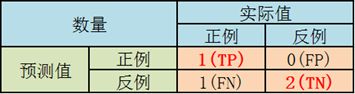
TPR = TP/(TP+FN) = 0.5
FPR = FP/(TN+FP) = 0

心得

用下面描述表示TPR和FPR的计算过程，更容易记住
• TPR：真实的正例中,被预测正确的比例,其实就是召回率
• FPR：真实的反例中，被预测正确的比例
最理想的分类器，就是对样本分类完全正确，即FP=0，FN=0。所以理想分类器TPR=1，FPR=0。

八、AUC

3.1AUC值的定义

AUC值为ROC曲线所覆盖的区域面积，显然，AUC越大，分类器分类效果越好。
　　AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
　　0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
　　AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
　　AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

3.2AUC值的物理意义

假设分类器的输出是样本属于正类的socre（置信度），则AUC的物理意义为，任取一对（正、负）样本，正样本的score大于负样本的score的概率。

3.3AUC值的计算

（1）第一种方法：AUC为ROC曲线下的面积，那我们直接计算面积可得。面积为一个个小的梯形面积之和，计算的精度与阈值的精度有关。
　　（2）第二种方法：根据AUC的物理意义，我们计算正样本score大于负样本的score的概率。取NM（N为正样本数，M为负样本数）个二元组，比较score，最后得到AUC。时间复杂度为O(NM)。
　　（3）第三种方法：与第二种方法相似，直接计算正样本score大于负样本的score的概率。我们首先把所有样本按照score排序，依次用rank表示他们，如最大score的样本，rank=n(n=N+M)，其次为n-1。那么对于正样本中rank最大的样本（rank_max），有M-1个其他正样本比他score小，那么就有(rank_max-1)-(M-1)个负样本比他score小。其次为(rank_second-1)-(M-2)。最后我们得到正样本大于负样本的概率为：

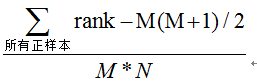
时间复杂度为O(N+M)。