基于D3Q19模型的LBM流体模拟

 

 

在CUDA上实现基于D3Q19模型的LBM流体模拟方法简介

--cyrosly与2009.05.14下午

 

LBM（Lattice Boltzmann Model）方法简介：

  LBM是始与上世纪80年代末起源于70年代的LGA（格子气自动机）理论模型，并最终从90年代初开始趋于成熟（在适定的范围内）的一种流体计算的介观方法（处于微观与宏观之间），从本质上讲，它比N-S方程的描述更本质化。LBM是一种基于统计物理学方法，事实上我们这里所说的LBM是为了简化Bolztmann方程的求解而进行适当但确异常合理和有效的计算模型，因为在该模型中不存在非线性项因而不存在传统数值方法（如预处理共轭梯度发和多重网格法）的数值发散问题，也即内迭代收敛问题。所谓内迭代收敛是指在某个当前的时间步在有限步之后是否可以得到当前流场的正确解（例如当我们在某个时间点上运行N次PCG解算器，这N次迭代并非是按时间方向向前推进，而是一个数学上的N次计算步骤）。虽然如此，LBM和传统方法一样也存在所谓的外迭代收敛问题；外迭代是指流场在整个时空尺度上是否可以在有限步之后收敛与平衡状态，也就是说在时间方向上流场收敛与稳态的快慢。此外LBM目前基本只适用于低March数不可压缩（或允许存在小尺度可压缩性）的情况，对于可压缩流体模型还未成熟，不过已经有很多这方面的研究发表。与传统数值方法相比LBM的另一个优点是对复杂边界的适应性，但对于自由表面LBM目前仍然没有完美的解决方法，一般和传统方法一样采用level set。

 

LBM计算模型：

 目前常用的规则网格模型有D2Q9，D3Q13，D3Q15，D3Q19（还有D1Q3，D2Q5，D3Q27），

当然还有各种非规则以及类似于传统网格划分的自适应格子布局。有兴趣的可以参考下郭照立郑楚光合编的《格子Bolztmann方法的原理及应用》。

           

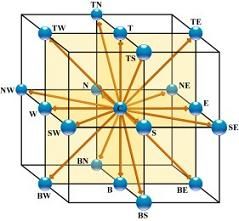
  LB Model D2Q9                                          LB Model D3Q19

 

上面分别是D2Q9和D3Q19的LBM规则格子模型。下面按方向给出几种常用格子的布局。

为此我们先有如下约定：

 pA:A轴正方向 nA:A轴负方向;A={X,Y,Z}

 E={e0,e1,e2…,en}:格子运动矢量

 Oe:指向格子自身的矢量

于是：

D2Q9 ：{ Oe , nX , pX , nY ,pY , nXnY, nXpY , pXnY, pXpY }

 

 

D3Q15 { Oe ,

nX , pX , nY , pY , nZ , pZ ,      //主轴方向

nXnYnZ , nXnYpZ , nXpYnZ , nXpYpZ , //格子正方体的8最长个对角线

pXnYnZ , pXnYpZ , pXpYnZ , pXpYpZ

          }

 

D3Q19: { Oe ,

nX , pX , nY , pY , nZ , pZ , //主轴方向

nXnY , nXpY , pXnY , pXpY ,  //与3个主轴共面的对角线

nYnZ , nYpZ , pYnZ , pYpZ ,

nZnX , nZpX , pZnX , pZpX

           }

  

LBGK动量方程为：

∆f=Ω,

∆f为迁移项，Ω为碰撞项

:

f(x+ei*δt,t+δt)-f(x,t)=—(1/ς)*(f(x,t)-feq(u,ρ))(1)

或

fnew= fcurr-Ω，feq为速度的平衡态分布

ς是松弛时间变量（我们这里主要针对单松弛时间法的LBGK模型，也有MRT(Multi Relaxtion Time)）

它对应与N-S方程的黏度项:

 ς=(3.f*kinetic_visc+0.5f)

其中kinetic_visc是动力学黏度，它的计算有赖于Reyholds数（马赫数）.

 

各种DnQm的Boltzmann格子模型的feq可统一表达成形式：

 

 

feq_i=ω_i*ρ*(1+(e_i•u_i)/(cs^2)+((e_i•u_i)^2)/(2*(cs^4))+(u_i^2)/(2*(cs^2))(2)

 ω是权重，满足归一化条件，即：

  ∑ω=1

cs是一个与声速有关的标量，对于前面提到的模型统一取为c/√3,c是由格子物理尺度决定的单位动力学速度的模。

 

不同模型的取值如下：

 

D2Q9：

 中心点 ：4/9

 主轴方向：1/9

 对角线上：1/36

 

D3Q15：

 中心点       ：2/9

 主轴方向     ：1/9

 最长对角线方向：1/72

 

D3Q19：

 中心点             ：1/3

 主轴方向           ：1/18

 与主平面共面的对角线：1/36

 

D3Q27：

 中心点             ：8/27

 主轴方向           ：2/27

 与主平面共面的对角线：1/54

 最长对角线         ：1/216

 

在LBM方法中宏观速度和密度是统计均值得到的：

 

 ρ=∑feq , ρu=∑feq•e_i (3)

 

现在需要的基本都有了，于是有如下模拟算法：

 

start:

0->给定初始速度和密度,然后通过(2)式初始化包分布

1->进入主循环

1.0->在当前时间步通过(3)式计算得到流场的宏观速度

1.1->根据边界条件更新平衡态包分布

1.2->执行碰撞

1.3->执行迁移

  ->如果流场没有收敛于平衡状态，跳转到1.0步继续执行

        ->否则结束

  

 对于障碍物边界可以使用[R5]中的FH格式或MLS和YMS格式，对于非工程领域的实时CG模拟足够了

 

感觉有些乱，事实上我在开始写这篇文章时几乎不知道接下来往哪里写，于是顺其自然的一气呵成。可能逻辑上有些乱，但对于不善于写文章的我来说这也相当自以为是的。呼，累了，就此结束吧。

 

另：感谢google为我节省了一些画图的时间（上面2个DnQm模型图片）

 

Reference:

 

[R0]郭照立郑楚光: <<格子Bolztmann方法的原理及应用>>

[R1]陈飞国,葛蔚,李静: <<复杂多相流动分子动力学模拟在GPU上的实现>>

[R2] Tolke: <<Implementation of a Lattice Boltzmann kernel using the Compute Unified Device Architecture developed by nVIDIA>>

 

[R3] Jonas Tölke, Jannis Linxweiler, Sebastian Geller, Manfred Krafczyk:

<>

 

[R4] Samuel Williams?y, Jonathan Carter?, Leonid Oliker? John Shalf?, Katherine Yelick:

<>

 

[R5] Wei Li ,Zhe Fan, Xiaoming Wei, and Arie Kaufman:

<>

 

[R6] Lan Shi, Li Yi & Liyuan Zhang:

<>

 

[R8] Ye Zhao:<>

 

[R9] V. Heuveline ,J.-P. Weiß:

<>