LambdaFM:一种在深度学习模型架构融合pairwise的策略
今天的博客主要参考了2016年的会议CIKM的paper《LambdaFM: Learning Optimal Ranking with Factorization Machines Using Lambda Surrogates》。
首先我想说一点常识知识,即本博客讲的内容涉及到了Learning to Rank领域的相关知识,其中Learning to Rank是一类算法框架包含了:Pointwise,Pairwise和Listwise三种方法。
其中pairwise是一种思想方法,该思想最常用的地方是搜索场景,相比于point wise(就是常说的交叉熵)pairwise更多的是强调两个商品之间的相对排序关系而不是单个样本的绝对预测结果,目前常见的方法有LambdaRank,RankNet等开源算法;而listwise则是强调全局的排序顺序和目标一致,但是同样它的训练复杂度也是最高的。
在搜索场景中,Pairwise是最常用的优化目标,下面先讲一下Pairwise的基础知识。在Pairwise优化目标下,训练样本是一个pair ( i , j ) {(i,j)} (i,j),标签 P i j P_{ij} Pij代表了用户喜欢i商品高于j商品的概率,即如果用户更喜欢i则有 P i j = 1 P_{ij}=1 Pij=1,如果用户用户更喜欢j则有 P i j = 0 P_{ij}=0 Pij=0,如果用户对i和j的喜欢程度一样则有 P i j = 0.5 P_{ij}=0.5 Pij=0.5,那么最终损失函数的定义如下:
L = ∑ u ∈ U ∑ i ∈ I ∑ j ∈ J − P i j l o g P i j − ( 1 − P i j l o g ( 1 − P i j ) ) L=\sum_{u\in U}\sum_{i\in I}\sum_{j\in J}-P_{ij}logP_{ij}-(1-P_{ij}log(1-P_{ij})) L=∑u∈U∑i∈I∑j∈J−PijlogPij−(1−Pijlog(1−Pij))
其实就是交叉熵,不过概率是两个pair样本之间的优先级关系,其中
P i j = 1 1 + e x p ( − σ ( y ( x i ) − y ( x j ) ) ) P_{ij}=\frac{1}{1+exp(-\sigma(y(x_i)-y(x_j)))} Pij=1+exp(−σ(y(xi)−y(xj)))1
其中 σ \sigma σ是一个标量,决定了sigmoid函数的shape,将该式带入上述的损失函数,同时为了简化公式起见,假设在构造样本对 ( i , j ) (i,j) (i,j)时,都有 i > j i>j i>j,则有:
L = ∑ u ∈ U ∑ i ∈ I ∑ j ∈ J l o g ( 1 + e x p ( − σ ( y ( x i ) − y ( x j ) ) ) ) L=\sum_{u\in U}\sum_{i\in I}\sum_{j\in J}log(1+exp(-\sigma(y(x_i)-y(x_j)))) L=∑u∈U∑i∈I∑j∈Jlog(1+exp(−σ(y(xi)−y(xj))))
如果对模型参数 θ \theta θ求导则有 ∂ L ( i , j ) ∂ θ = λ i , j ( ∂ ( y ( x i ) ) ∂ θ − ∂ ( y ( x j ) ) ∂ θ ) \frac{\partial L(i,j)}{\partial \theta}=\lambda_{i,j}(\frac{\partial(y(x_i))}{\partial \theta}-\frac{\partial(y(x_j))}{\partial \theta}) ∂θ∂L(i,j)=λi,j(∂θ∂(y(xi))−∂θ∂(y(xj)))
其中 λ i j \lambda_{ij} λij可以被看做是梯度更新的权重
即 λ i j = ∂ L ( i , j ) ∂ ( y ( x i ) − y ( x j ) ) = − σ 1 + e x p ( σ ( y ( x i ) − y ( x j ) ) ) \lambda_{ij}=\frac{\partial L(i,j)}{\partial (y(x_i)-y_(x_j))}=-\frac{\sigma}{1+exp(\sigma(y(x_i)-y(x_j)))} λij=∂(y(xi)−y(xj))∂L(i,j)=−1+exp(σ(y(xi)−y(xj)))σ
现在我们把pairwise放到FM框架之下,首先给出FM的数学公式:
y ( x ) = w 0 + ∑ k = 1 n w k x k + 1 2 ∑ f = 1 d ( ( ∑ k = 1 n v k , f x k ) 2 − ∑ k = 1 n v k , f 2 x k 2 ) y(x)=w_0+\sum_{k=1}^nw_kx_k+\frac{1}{2}\sum_{f=1}^d((\sum_{k=1}^nv_{k,f}x_k)^2-\sum_{k=1}^nv_{k,f}^2x_k^2) y(x)=w0+∑k=1nwkxk+21∑f=1d((∑k=1nvk,fxk)2−∑k=1nvk,f2xk2)
如果把标准pairwise的和FM结合,则有
1 ∂ y ( x i ) ∂ θ = x k i \frac{\partial y(x_i)}{\partial \theta}=x_k^i ∂θ∂y(xi)=xki 当 θ \theta θ 是 w k w_k wk
2 ∂ y ( x i ) ∂ θ = x k i ∑ l = 1 n v l , f x l i − v k , f x k i 2 \frac{\partial y(x_i)}{\partial \theta}=x_k^i \sum_{l=1}^nv_{l,f}x_{l}^i-v_{k,f}x_k^{i^2} ∂θ∂y(xi)=xki∑l=1nvl,fxli−vk,fxki2 当 θ \theta θ 是 v k , f v_{k,f} vk,f
那么在推荐场景下,如果构造pair对样本呢?

其实到这里,FM+pairwise最核心的东西已经讲完了,但是如果直接这样使用的话,效果往往是不理想的,原因如下图所示:
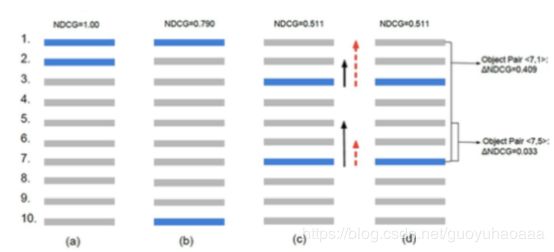
这里是以NDCG为最终优化目标为例进行说明,其中NDCG衡量指标的公式为: N D C G p = D C G p I D C G p NDCG_p=\frac{DCG_p}{IDCG_p} NDCGp=IDCGpDCGp,其中 D C G p = ∑ i = 1 p 2 r e l i − 1 l o g 2 ( i + 1 ) DCG_p=\sum_{i=1}^p\frac{2^{rel_i}-1}{log_2(i+1)} DCGp=∑i=1plog2(i+1)2reli−1, I D C G p = ∑ i = 1 ∣ R E L ∣ 2 r e l i − 1 l o g 2 ( i + 1 ) IDCG_p=\sum_{i=1}^{|REL|}\frac{2^{rel_i}-1}{log_2(i+1)} IDCGp=∑i=1∣REL∣log2(i+1)2reli−1,其中 r e l i rel_i reli是第i个商品的相关程度评分,i为位置序号,可以看出越相关的商品排在越靠前的位置就会得到更大的NDCG值,IDCG代表了理论上最优的排序方式(图中a方式),即完全按照相关程度从1 到 后排序。
可以看出NDCG不是一个可以直接求导的形式,所以很难直接放到损失函数里去,但是如果不考虑NDCG的值就会出现上图情形,即从b到c的操作过程,即在某一次迭代优化之后,虽然排列错误的pair数减少了(因为之前的损失函数目前就是减少排错的pair总数),但是NDCG却下降了。
在LambdaRank中为了解决这个问题,在最后求导的时候,将梯度更新权重 λ i j \lambda_{ij} λij乘以了 ∣ Δ N D C G ∣ |\Delta NDCG| ∣ΔNDCG∣,即变成了 ∣ Δ N D C G ∣ λ i j |\Delta NDCG|\lambda_{ij} ∣ΔNDCG∣λij,这个 ∣ Δ N D C G ∣ |\Delta NDCG| ∣ΔNDCG∣意思就是如果将i和j互换位置,最终这个预测list的整体NDCG值的变化幅度。这个放到搜索场景中共,list前后变化的NDCG值是可以算出来的;但是放到推荐系统下,其本身目标可能就不再是NDCG了,所以需要新的给最后梯度加权的方式,和推荐场景类似,既然 Δ N D C G \Delta NDCG ΔNDCG越大说明样本对 ( i , j ) (i,j) (i,j)对最后网络权重更新的贡献越大,我在前面说过,这个场景下的pair样本对构造过程中在选择样本对的时候,可以把这个权值体现到最终抽样的概率上,即越是重要的样本对,越会有更高的概率被选中,这样既然样本对的生成不再是等概率的,而是根据目标有了一定的偏好,那么就变相的相当对增加了权重(更重要的样本对会有更高的概率被抽中,那么自然对最后的损失函数有更大的影响),这样就把问题转换到了如何合理的构造样本对的问题上来了,作者给出了3种参考方式:
方式一 Static & Context-independent Sampler
在构造用户商品的 ( i , j ) (i,j) (i,j)的时候,在选择j时不再依靠uniform分布了,而是对每一个商品按照概率进行抽样生成,而这个概率分布构造如下:
p j = > e x p ( − r ( j ) + 1 ∣ I ∣ + p ) , p ∈ ( 0 , 1 ] p_j => exp(-\frac{r(j)+1}{|I|+p}),p\in (0,1] pj=>exp(−∣I∣+pr(j)+1),p∈(0,1]
其中 r ( j ) r(j) r(j)是商品受欢迎程度的排名,越受欢迎这个值越小, ∣ I ∣ |I| ∣I∣是商品总数,会发现这个公式让更被受欢迎的商品拥有了更高的权重,这个其实是符合直觉的,就是是那些受欢迎的但是用户没有购买的样本会比不受欢迎且用户没有点击的样本更有价值一些。商品的受欢迎程度是一个全局的固定值,故这种方式速度虽然很简单,但是没有考虑到不同用户不同上下文的区别;
方式二 Dynamic & Context-aware Sampler

其实流程都在图里了,和第一种方式一样,在这种方式中也是对样本对 ( i , j ) (i,j) (i,j)中的j生成采用概率分布 P ( j ) P(j) P(j),只不过采用和第一种全局固定不一样的方法,过程都在图中了,就不再赘述了,它们都是把那些拥有较高受欢迎程度和较高购买概率但是没有买的j赋予更高的采样权值;
方式三 Rank-aware Weighted Approximation
方式三是另一个思路即想办法去对样本对 ( i , j ) (i,j) (i,j)中的i生成采用概率 P ( i ) P(i) P(i),具体过程如下图所示:

虽然图中的流程看上去很多公式很复杂,但可以看到关键点在梯度更新的权重计算公式上 ∑ r = 0 ∣ I ∣ − 1 T 1 r + 1 Γ ( I ) \frac{\sum_{r=0}^{\frac{|I|-1}{T}} \frac{1}{r+1}}{\Gamma(I)} Γ(I)∑r=0T∣I∣−1r+11,其中 Γ ( I ) = ∑ r ∈ I 1 r + 1 \Gamma(I)=\sum_{r\in I}\frac{1}{r+1} Γ(I)=∑r∈Ir+11,而且其实会发现步骤9到步骤13其实是在估算这个T,这个T是什么意思呢,这样设置又有什么意义呢?其实这里作者想做的是让那些被用户购买的但是在全部商品list中排名又不高的pair对中的i有更高的优先级,但是如何知道目标i在购买list中的排名呢,这个T就是来估算排名的。
其实这个T从计算步骤看是多少次随机能找出一个j,虽然没有被用户购买但是在当前模型参数的计算得分加上一个 ε \varepsilon ε超过了i在当前模型参数下的得分,那么这个i在全部商品中的大致排名就是 ∣ I ∣ − 1 T \frac{|I|-1}{T} T∣I∣−1,而分母的 Γ ( I ) \Gamma(I) Γ(I)就是归一化因子。这个也是很符合直觉的,这些被用户购买但是在当前模型参数下计算得分不高的那些商品同样具有更高的权重,应该被赋予更高的采样概率。
最后作者通过一系列的实验证明了模型的有效性。