PyTorch 学习笔记（三）：线性回归、logistic回归

通过前面两篇笔记的学习已经基本了解了PyTorch里面的基本处理对象、运算操作、自动求导、以及数据处理方法、模型的保存和加载等基础知识。下来就是实战部分了。

一. 线性回归

1. 一维线性回归

给定数据集 $D=\left\{(x_1,y_1),(x_2,y_2),(x_3,y_3),...,(x_m,y_m)\right\}$，线性回归希望能够优化出一个好的函数 f(x)，使得$f(x_i)=w{x}_i+b$能够与$y_i$尽可能接近。

# 一维线性回归

import numpy as np
import matplotlib.pyplot as plt
import torch
from torch.autograd import Variable
from torch import nn, optim
# 给定数据集
x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168], [9.779], [6.182], [7.59],
                    [2.167], [7.042], [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)
y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573], [3.366], [2.596], [2.53], [1.221],
                    [2.827], [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)

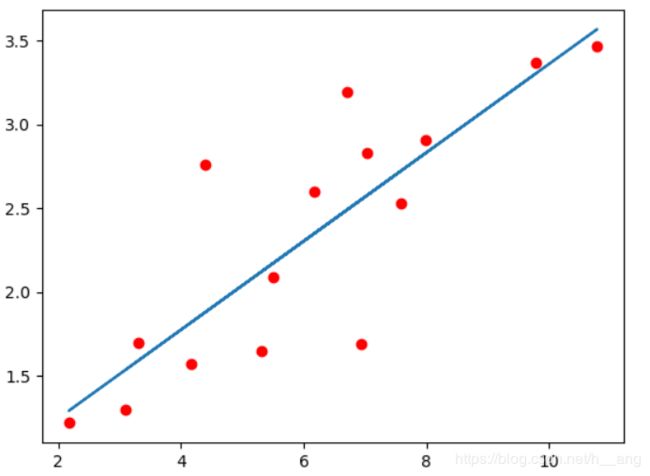
# 数据可视化
plt.plot(x_train, y_train, 'ro', label='Original data')

# 将训练集由numpy.array转换为Tensor类型
x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)

# 建立模型
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)   # input and output is 1 dimension

    def forward(self, x):
        out = self.linear(x)
        return out

# 如果GPU加速，可以通过model.cuda()将模型放到GPU上
if torch.cuda.is_available():
    model = LinearRegression().cuda()
else:
    model = LinearRegression()

# 定义损失函数
criterion = nn.MSELoss()   # 平方误差损失函数
optimizer = optim.SGD(model.parameters(), lr=1e-3)

# 开始训练
num_epoches = 100
for epoch in range(num_epoches):
    # 将数据变成Variable放入计算图中
    if torch.cuda.is_available():
        inputs = Variable(x_train).cuda()
        target = Variable(y_train).cuda()
    else:
        inputs = Variable(x_train)
        target = Variable(y_train)

    # forward
    out = model(inputs)
    loss = criterion(out, target)
    # backward
    optimizer.zero_grad()   # 梯度归零
    loss.backward()    # 反向传播，自动求导得到每个参数的梯度
    optimizer.step()     # 梯度做进一步参数更新

    if (epoch+1) % 20 == 0:
        print("Epoch[{}/{}], loss: {:.6f}".format(epoch+1, num_epoches, loss.data))

# 开始做预测
# 将模型变成测试模式，这是因为有一些层操作，比如Dropout和BatchNormalization在训练和测试时是不一样的，所以我们需要通过这样一个操作来转换这些不一的层
model.eval()
# 计算预测值
predict = model(Variable(x_train))
# 将预测值从Tensor转换为numpy类型
predict = predict.data.numpy()
# 画出数据线
plt.plot(x_train.numpy(), predict, label='Fitting Line')
plt.show()

运行结果：

2. 多维线性回归

更一般的情况是多维线性回归，比如像前文描述的，我们有d个属性，试图学得最优的函数f(x)。

对于线性回归求解最优参数，有两种方法，一种是利用正规方程组，另一种是利用梯度下降算法，具体推导可以在我以前的博客中学习：https://blog.csdn.net/h__ang/article/details/88660538

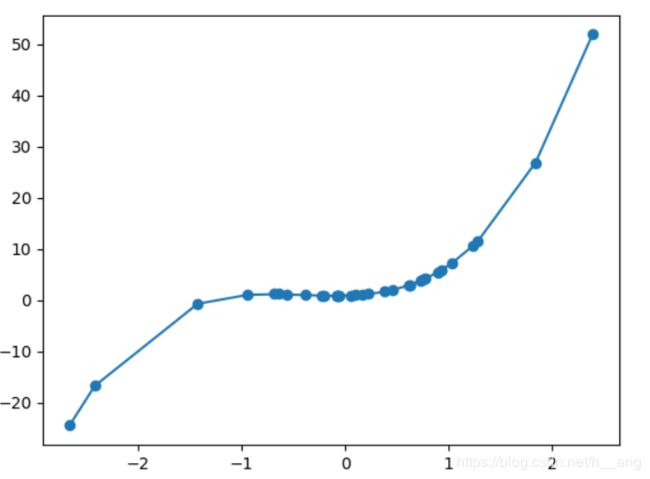
1中的线性回归模型的拟合能力很明显不够强，我们需要提高模型的拟合能力，使用更复杂的模型，这里我们尝试用高次多项式而不是简单的一次线性多项式。

不妨设置参数方程：$y=b+w_1{x}_1+w_2{x}^2+w_3{x}^3$
那么就相当于原来一维的训练数据x_train变成了三维，原来的每一个数据x变成了$\left[x,x^2,x^3\right]$。

import torch
from torch import nn, optim
from torch.autograd import Variable

# 构造特征
def make_features(x):
    x = x.unsqueeze(1)
    return torch.cat([x**i for i in range(1, 4)], 1)

# 定义好真实的函数
W_target = torch.FloatTensor([0.5, 3, 2.4]).unsqueeze(1)    # 将原来的tensor大小由3变成(3, 1)
b_target = torch.FloatTensor([0.9])
print(W_target)
def f(x):
    return x.mm(W_target) + b_target

# 得到训练集合
def get_batch(batch_size=1):
    random = torch.randn(batch_size)
    x = make_features(random)
    y = f(x)
    if torch.cuda.is_available():
        return Variable(x).cuda(), Variable(y).cuda()
    else:
        return Variable(x), Variable(y)

# 构建模型
class poly_model(nn.Module):
    def __init__(self):
        super(poly_model, self).__init__()
        self.poly = nn.Linear(3, 1)
    def forward(self, x):
        out = self.poly(x)
        return out

if torch.cuda.is_available():
    model = poly_model().cuda()
else:
    model = poly_model()

# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)

# 开始训练
epoch = 0
while True:
    # get data
    batch_x, batch_y = get_batch()
    # forward
    output = model(batch_x)
    loss = criterion(output, batch_y)
    print(loss)
    print_loss = loss.data.float()
    # Reset gradients
    optimizer.zero_grad()
    # backward
    loss.backward()
    # update parameters
    optimizer.step()
    epoch += 1
    if print_loss < 1e-3:
        print("Loss: {} after {} batches".format(print_loss, epoch))
        print("Actual function: y = 0.90 + 0.50x + 3.00*x^2 + 2.40*x^3")
        for name,param in model.named_parameters():
            print(name, param)
        break

运行结果：

二. 逻辑斯蒂(Logistic)回归

Logistic回归不仅可以解决二分类问题，也可以解决多分类问题，但是二分类问题最为常见同时也具有良好的解释性。对于二分类问题，Logistic回归的目标是希望找到一个区分度足够好的决策边界，能够将两类很好的分开。

关于Logistic的具体推导详情请见：https://blog.csdn.net/h__ang/article/details/88672590

import torch
import matplotlib.pyplot as plt
from torch import nn, optim
from torch.autograd import Variable
import numpy as np
def get_dataset():
    with open('data.txt', 'r') as f:
        data_list = f.readlines()
        data_list = [i.split('\n')[0] for i in data_list]
        data_list = [i.split(',') for i in data_list]
        x_train = [[float(i[0]), float(i[1])] for i in data_list]
        y_train = [float(i[2]) for i in data_list]
        return x_train, y_train

def plot_data(x, y):
    pos = np.where(y == 1.0)
    neg = np.where(y == 0.0)
    # 分别用红色和蓝色对两种类的数据点做出标记
    plt.plot(x[pos, 0], x[pos, 1], 'ro', label='x_0')
    plt.plot(x[neg, 0], x[neg, 1], 'bo', label='x_1')

class LogisticRegression(nn.Module):
    def __init__(self):
        super(LogisticRegression, self).__init__()
        self.lr = nn.Linear(2, 1)
        self.sm = nn.Sigmoid()
    def forward(self, x):
        out = self.lr(x)
        #print(x)
        out = self.sm(out)
        return out



if __name__ == "__main__":
    # 从'data.txt’文件夹中获取训练数据和标签
    x_train, y_train = get_dataset()
    # 将其转换为numpy.array类型,这里一定是np.float32,否则默认是np.float64，后面就会报错
    x_train = np.array(x_train, dtype=np.float32)
    y_train = np.array(y_train, dtype=np.float32)
    # 可视化原始数据
    plot_data(x_train, y_train)
    # 将array的数据转换为Tensor类型
    x_train = torch.from_numpy(x_train)
    y_train = torch.from_numpy(y_train).unsqueeze(1)
    #print(x_train)
    if torch.cuda.is_available():
        logistic_model = LogisticRegression().cuda()
    else:
        logistic_model = LogisticRegression()
    # 定义损失函数和优化器
    criterion = nn.BCELoss()      # nn.BCELoss是二分类的损失函数
    optimizer = optim.SGD(logistic_model.parameters(), lr=1e-3, momentum=0.9)
    # 训练模型
    for epoch in range(50000):
        # 转换为Variable
        if torch.cuda.is_available():
            x_train = Variable(x_train).cuda()
            y_train = Variable(y_train).cuda()
        else:
            x_train = Variable(x_train)
            y_train = Variable(y_train)
        # forward
        out = logistic_model(x_train)
        loss = criterion(out, y_train)
        # 计算准确率
        mask = out.ge(0.5).float()
        correct = (mask == y_train).sum().float()
        acc = correct/x_train.size(0)
        # backward
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        #print(loss.data)
        if (epoch+1) % 1000 == 0:
            print('*'*10)
            print("eopch {}, loss is {:.4f}, acc is {:.4f}".format(epoch+1, loss, acc))
    # 将训练得到的参数可视化
    w0, w1 = logistic_model.lr.weight.data.numpy()[0]
    print(w0, w1)
    b = logistic_model.lr.bias.data.numpy()[0]
    print(b)
    plot_x = np.arange(30, 100, 0.1)
    plot_y = (-w0 * plot_x - b) / w1
    plt.plot(plot_x, plot_y)
    plt.show()

运行，可以看到，找到了一条线将两类样本分开：

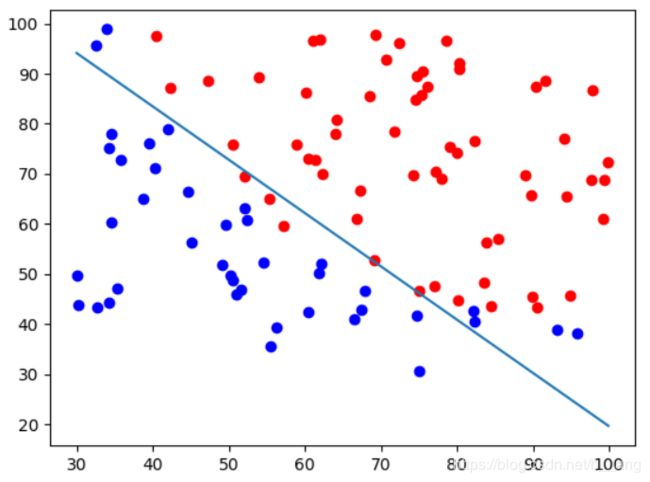
以上内容皆为廖星宇编著的《深度学习入门之PyTorch》这本书上的内容，代码部分略有改动。