【PyTorch】使用PyTorch创建卷积神经网络并在CIFAR-10数据集上进行分类

前言

在深度学习的世界中，图像分类任务是一个经典的问题，它涉及到识别给定图像中的对象类别。CIFAR-10数据集是一个常用的基准数据集，包含了10个类别的60000张32x32彩色图像。在本博客中，我们将探讨如何使用PyTorch框架创建一个简单的卷积神经网络（CNN）来对CIFAR-10数据集中的图像进行分类。

在下一篇博客中，我们将尝试不断优化模型结构和训练过程，以达到更高的准确率和性能。

引用

关于卷积神经网络的原理，感兴趣的请参阅我的另一篇博客，里面只使用numpy和基础函数组建了一个卷积神经网络模型，并完成训练和测试
【手搓深度学习算法】从头创建卷积神经网络

背景

卷积神经网络是深度学习中用于图像识别和分类的一种强大工具。它们能够自动从图像中提取特征，并通过一系列卷积层、池化层和全连接层来学习图像的复杂模式。

CIFAR-10数据集包含了飞机、汽车、鸟类、猫、鹿、狗、青蛙、马、船和卡车等10个类别的图像。每个类别有6000张图像，其中50000张用于训练，10000张用于测试。

代码解析

我们的目标是构建一个能够处理CIFAR-10数据集的CNN模型。以下是我们的模型结构和数据处理流程的简要概述：

数据预处理

我们首先定义了unpickle函数来加载CIFAR-10数据集的批次文件。read_data函数用于读取数据，将其转换为适合卷积网络输入的格式，并进行归一化处理。我们还提供了一个选项来将图像转换为灰度。

def unpickle(file):
    import pickle
    with open(file, 'rb') as fo:
        dict = pickle.load(fo, encoding='bytes')
    return dict

def read_data(file_path, gray = False, percent = 0, normalize = True):
    data_src = unpickle(file_path)
    np_data = np.array(data_src["data".encode()]).astype("float32")
    np_labels = np.array(data_src["labels".encode()]).astype("float32").reshape(-1,1)
    single_data_length = 32*32 
    image_ret = None
    if (gray):
        np_data = (np_data[:, :single_data_length] + np_data[:, single_data_length:(2*single_data_length)] + np_data[:, 2*single_data_length : 3*single_data_length])/3
        image_ret = np_data.reshape(len(np_data),32,32)
    else:
        image_ret = np_data.reshape(len(np_data),32,32,3)
    
    if(normalize):
        mean = np.mean(np_data)
        std = np.std(np_data)
        np_data = (np_data - mean) / std
    
    if (percent != 0):
        np_data = np_data[:int(len(np_data)*percent)]
        np_labels = np_labels[:int(len(np_labels)*percent)]
        image_ret = image_ret[:int(len(image_ret)*percent)]
    num_classes = len(np.unique(np_labels))
    np_data, np_labels = convert_to_conv_input(np_data, np_labels)
    return np_data, np_labels, num_classes, image_ret 

网络结构

Conv类定义了我们的CNN模型，它包含一个卷积层、一个最大池化层、一个ReLU激活函数和一个全连接层。在forward方法中，我们指定了数据通过网络的流程。

class Conv(th.nn.Module):
    def __init__(self, *args, **kwargs) -> None:
        super(Conv, self).__init__()
        self.conv = th.nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3)
        self.pool = th.nn.MaxPool2d(kernel_size=2,stride=2)
        self.relu = th.nn.ReLU()
        self.linear = th.nn.Linear(16*15*15, 10)
        self.softmax = th.nn.Softmax(dim=1)
        
    def forward(self, x):
        x = self.conv(x) #32，16，30，30
        x = self.pool(x) #32，16，15，15
        x = self.relu(x)
        x = x.view(x.size(0), -1)
        x = self.linear(x)
        return x
    
    # 在predict函数中，额外调用了softmax，将线性层的10个特征值转化为概率，在前向传播中不用是因为pytorch中交叉熵函数自带了softmax
    def predict(self,x):
        x = self.forward(x)
        x = self.softmax(x)
        return x

卷积层、池化层、线性层的输入特征数量的计算方法

线性层的输入特征个数取决于前面层的输出。
具体来说，线性层的输入特征个数是卷积层和池化层处理后的输出特征图的总元素数量。

卷积层定义如下：

self.conv = th.nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3)

这里，in_channels=3 表示输入图像有3个颜色通道（RGB），out_channels=16 表示卷积层将输出16个特征图。

接下来是池化层：

self.pool = th.nn.MaxPool2d(kernel_size=2, stride=2)

kernel_size=2，表示池化窗口的大小是2x2。stride=2 表示池化操作的步长是2。

为了计算线性层的输入特征个数，我们需要知道卷积层和池化层之后的输出特征图的大小。这可以通过计算公式得到，或者通过在实际数据上运行网络的前向传播来确定。

计算公式如下：

对于卷积层，输出特征图的大小可以通过以下公式计算：

H_out = (H_in + 2 * padding - dilation * (kernel_size - 1) - 1) / stride + 1
W_out = (W_in + 2 * padding - dilation * (kernel_size - 1) - 1) / stride + 1

对于池化层，输出特征图的大小也可以通过类似的公式计算。

由于没有指定padding和dilation，查看函数定义可知它们的默认值分别是0和1。因此，如果输入图像的大小是32x32，卷积层之后的大小将是：

H_out = (32 - 1 * (3 - 1) - 1) / 1 + 1 = 30
W_out = (32 - 1 * (3 - 1) - 1) / 1 + 1 = 30

因此，卷积层的输出将有16个30x30的特征图。

然后，池化层将这些特征图的大小减半（因为kernel_size=2和stride=2），所以输出将是16个15x15的特征图。

最后，线性层的输入特征个数将是这些特征图的总元素数量：

num_features = out_channels * H_out_pool * W_out_pool = 16 * 15 * 15 = 3600

因此，线性层的正确定义应该是：

self.linear = th.nn.Linear(3600, num_classes)

训练过程

在main函数中，我们初始化了模型、损失函数和优化器。我们使用随机梯度下降（SGD）作为优化算法，并设置了学习率。接着，我们进入了训练循环，其中包括前向传播、损失计算、反向传播和权重更新。

loss_function = th.nn.CrossEntropyLoss()
optimizer = th.optim.SGD(conv_model.parameters(), lr = lr)

测试和评估

训练完成后，我们使用训练好的模型对测试数据进行评估，并计算准确率。我们还提供了一个predict方法，它在给定输入数据后返回模型的预测概率。

def predict(self,x):
        x = self.forward(x)
        x = self.softmax(x)
        return x

softmax激活函数

Softmax 激活函数是一种广泛使用的函数，它将一个实数向量转换为概率分布。在深度学习中，它常常用于多类别分类问题的输出层。

Softmax 函数的定义如下：

$$\text{softmax}(z{)}_i=\frac{e^{z_i}}{{\sum }_j{e}^{z_j}}$$

其中 $z$ 是输入向量，$z_i$ 是 $z$ 的第 $i$ 个元素，$\text{softmax}(z{)}_i$ 是输出向量的第 $i$ 个元素。

Softmax 函数的主要特性是它的输出是一个概率分布，即所有输出元素的值都在 $(0,1)$ 区间内，且所有输出元素的值之和为 1。这使得 Softmax 函数非常适合用于表示概率。

Softmax 函数的一个重要性质是它是连续的，且其导数容易计算。这使得 Softmax 函数在深度学习中的反向传播过程中非常有用。

Softmax 函数的导数如下：

$$\frac{\partial }{\partial z_i}\text{softmax}(z{)}_i=\text{softmax}(z{)}_i(1-\text{softmax}(z{)}_i)$$

这个导数表达式表明，对于 Softmax 函数的输出 $y_i$，其对输入 $z_i$ 的导数等于 $y_i(1-y_i)$。这个导数表达式在反向传播过程中非常有用，因为它可以直接用于计算梯度。

训练过程中没有使用softmax层，是应为torch的交叉熵损失函数已经包含了softmax的操作，如果叠加使用，可能得到错误的结果。

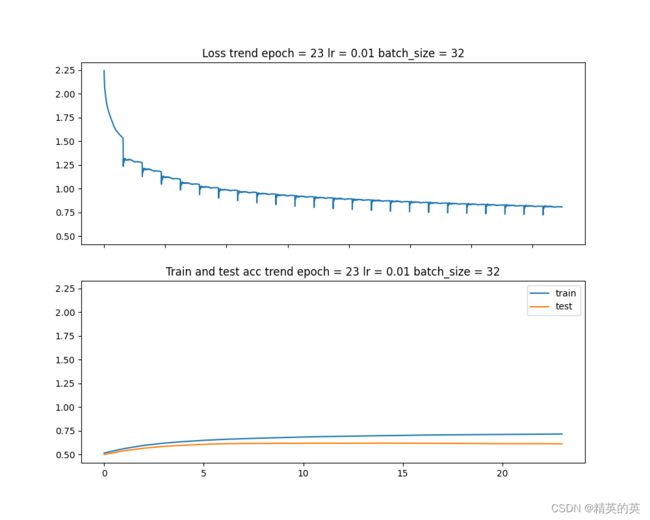
运行结果

作为一个简单的卷积模型，在测试集上得到了60%的准确率

完整代码

本文不提供完整代码，因为随着我的微调优化过程，已经没有这个版本的基线代码了，想要最终代码的欢迎阅读下一篇博客 “记一次卷积网络调优的过程”

注意点

• 数据预处理：确保数据被正确地加载和归一化，这对模型的训练效果至关重要。
• 模型结构：模型的层数和参数需要根据任务的复杂性来调整。过于简单的模型可能无法捕捉到数据中的复杂特征，而过于复杂的模型可能会导致过拟合。
• 损失函数：我们使用交叉熵损失函数，它适用于多类别分类问题。
• 优化器：在每次迭代前，记得清除累积的梯度，以避免错误的梯度更新。

可能的优化点

• 学习率调整：可以尝试使用学习率调度器来在训练过程中调整学习率，以改善模型的收敛速度和性能。
• 权重初始化：尝试不同的权重初始化方法，以帮助模型更快地收敛。
• 正则化技术：使用如Dropout、L2正则化等技术来减少过拟合。
• 数据增强：通过对训练图像进行随机变换（如旋转、缩放、裁剪等），可以增加模型的泛化能力。
• 更深的网络：考虑增加更多的卷积层和池化层来提取更复杂的特征。
• 批量归一化：在卷积层之后添加批量归一化层，以稳定训练过程并加速收敛。

结论

通过本博客，我们展示了如何使用PyTorch框架构建一个简单的CNN模型，并在CIFAR-10数据集上进行训练和测试。虽然我们的模型结构相对简单，但它为理解深度学习和图像分类提供了一个很好的起点。在下一篇博客中，我们将尝试不断优化模型结构和训练过程，以达到更高的准确率和性能。