ICML 2018 深度学习论文及代码集锦(10) 完结篇
[1] DCFNet: Deep Neural Network with Decomposed Convolutional Filters
Qiang Qiu, Xiuyuan Cheng, Robert Calderbank, Guillermo Sapiro
Duke University
http://proceedings.mlr.press/v80/qiu18a/qiu18a.pdf
这篇论文将卷积神经网络中的卷积滤波分解成预先固定基的截断式展开,即分解卷积滤波网络,这里的展开系数从数据中学习得到。这种结构不仅可以减少需要训练的参数,而且可以减少计算量,还可以利用基截断来实现滤波约束。DCFNet可以在保证准确率的前提下明显缩减模型参数,尤其利用Fourier-Bessel基时,甚至利用随机基也可以。DCFNet的表示随输入的变换具有一定的稳定性,并且对展开系数加以一般性假设时的表示稳定性可以得以证明。
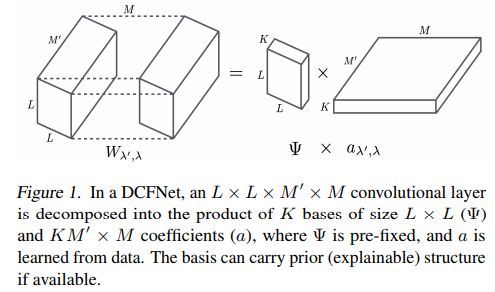
DCFNet的卷积层示例如下
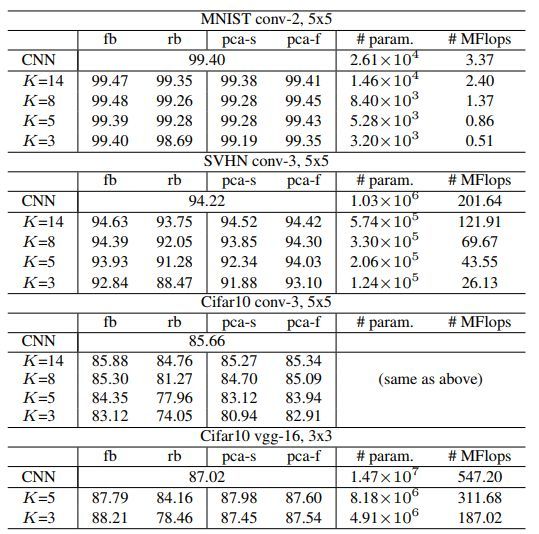
不同数据集的结果对比如下
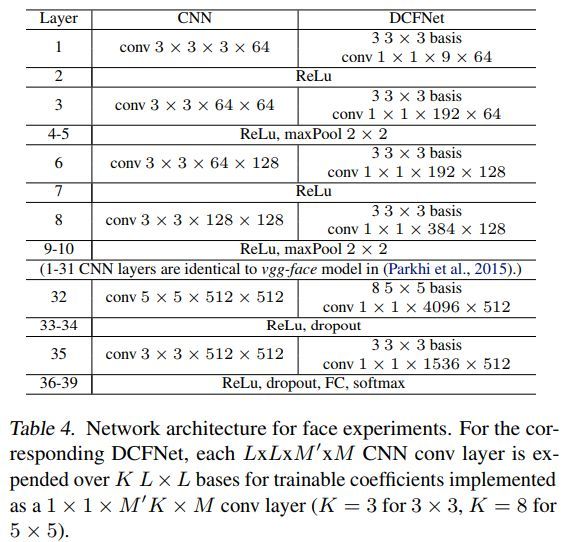
CNN与DCFNet结构对比如下
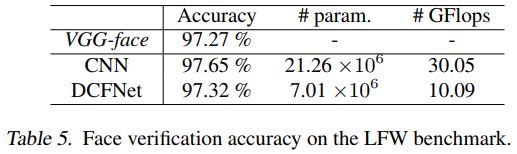
不同网络的效果对比如下
代码地址
https://github.com/xycheng/DCFNet
[2] StrassenNets: Deep Learning with a Multiplication Budget
Michael Tschannen, Aran Khanna, Anima Anandkumar
ETH Zürich, Amazon AI, Caltech
http://proceedings.mlr.press/v80/tschannen18a/tschannen18a.pdf
这篇论文在DNN层中进行端到端的学习,对矩阵成绩进行低成本的近似,将矩阵乘积映射为两层的和积网络(SPNs),并且从数据中学习其中的边权。SPNs将乘积和求和算子分离开来,这就使得乘积算子更加方便。这种方法结合知识升华并且利用DNN进行图像分类和语言模型,可以使得乘积算子大幅减少,并且同时可以保持模型的预测效果。另外,该框架可以重新发现Strassen矩阵乘积算法,对于2×2的矩阵相乘,只需7次乘积,而不是8次乘积。
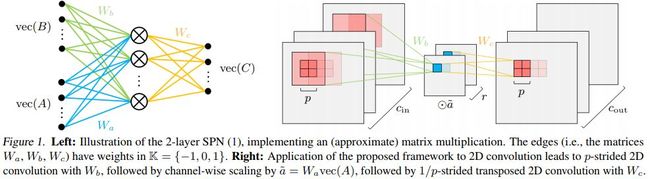
本文所提网络结构和spn结构对比如下
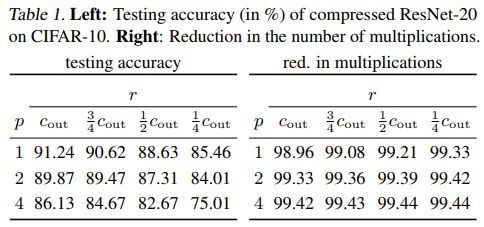
ResNet相关结果如下
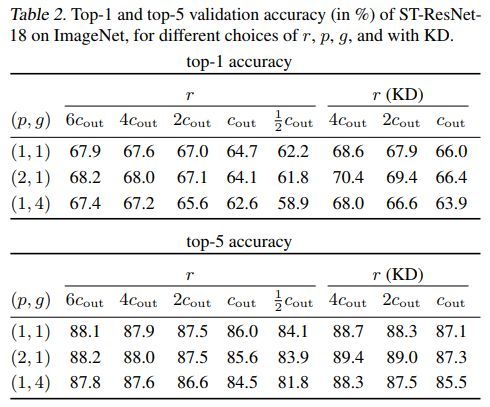
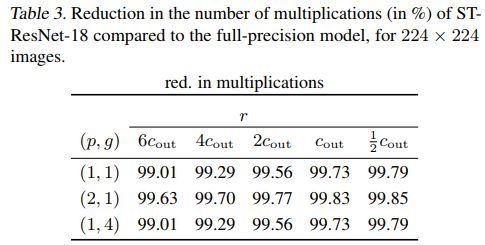
ST-ResNet结果如下
代码地址
https://github.com/mitscha/strassennets
[3] Deep k-Means: Re-Training and Parameter Sharing with Harder Cluster Assignments for Compressing Deep Convolutions
Junru Wu, Yue Wang, Zhenyu Wu, Zhangyang Wang, Ashok Veeraraghavan, Yingyan Lin
Texas A&M University, Rice University
http://proceedings.mlr.press/v80/wu18h/wu18h.pdf
这篇论文提出一种简单却高效的框架,该框架可以对权重进行k-means聚类进而可以对卷积进行压缩,压缩是通过权值共享得到的。该压缩过程只记录聚类中心和权重的下标。该论文还引入了一种新颖的基于谱放松的k-means约束,这样可以对难学的卷基层权重利用聚类中心来重新训练。
另外,这篇文章还提出一些指标来估计cnn硬件实现的能量损耗。将深层K-means用于若干cnn模型,可以进行一定程度的压缩和降低能量消耗,可以得到可观的效果。
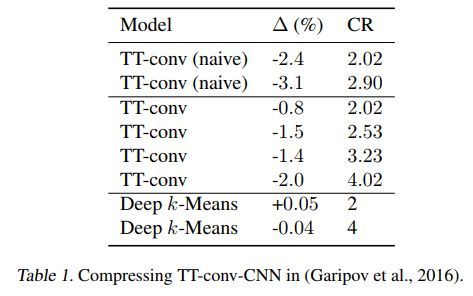
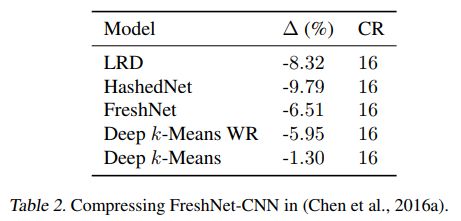
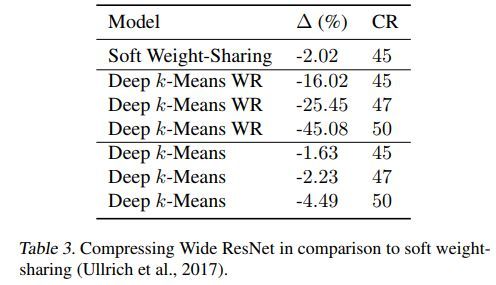
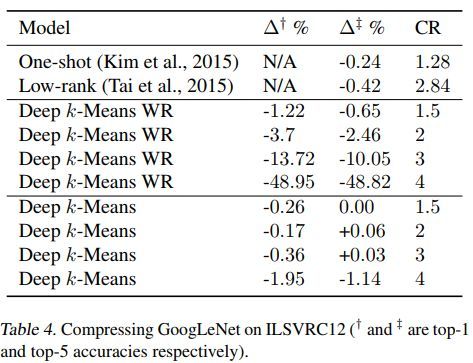
几种方法的对比如下
其中TT-conv 为Tensor Train (TT) Decomposition approach for convolutional kernel
代码地址
https://github.com/Sandbox3aster/Deep-K-Means-pytorch
[4] JointGAN: Multi-Domain Joint Distribution Learning with Generative Adversarial Nets
Yunchen Pu, Shuyang Dai, Zhe Gan, Weiyao Wang, Guoyin Wang, Yizhe Zhang, Ricardo Henao, Lawrence Carin
Facebook, Duke University, Microsoft Research
http://proceedings.mlr.press/v80/pu18a/pu18a.pdf
这篇文章提出一种新的GAN用于联合分布匹配。这种方法旨在学习多个随机变量的联合分布。该方法是通过在不同域之间学习条件分布来完成的,同时在每个独立的域中学习边际分布,该框架包含多个生成器,还包含一个独立的基于softmax的临界条件,都是通过对抗学习来联合训练的。所提框架可以从边际分布中进行采样,从随机变量子集中可以采样条件分布,从全联合分布中可以完全采样。
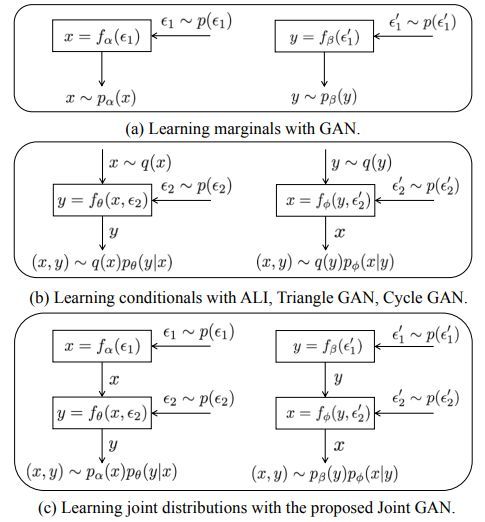
几种GAN的结构对比如下
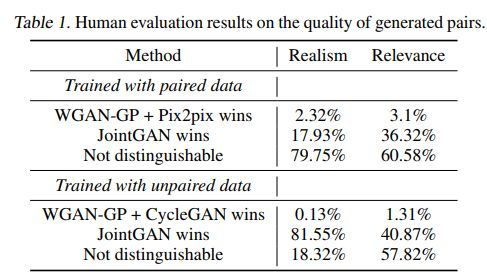
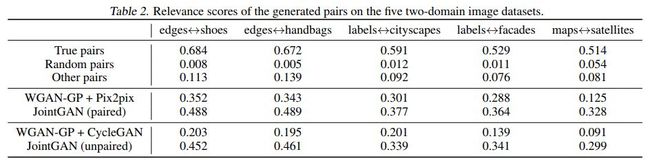
几种方法的效果对比如下
代码地址
https://github.com/sdai654416/Joint-GAN
[5] Semi-Amortized Variational Autoencoders
Yoon Kim, Sam Wiseman, Andrew C. Miller, David Sontag, Alexander M. Rush
Harvard University, Massachusetts Institute of Technology
http://proceedings.mlr.press/v80/kim18e/kim18e.pdf
这篇论文提出一种混合方法,利用AVI来初始化变分参数,并且利用随机变分推理来优化这些参数。值得注意的是,局部随机变分推理过程本身是可微的,因此,推理网络和生成式模型可以利用基于梯度的方法来端到端的训练。
最大化目标函数的算法步骤如下
算法简略步骤如下
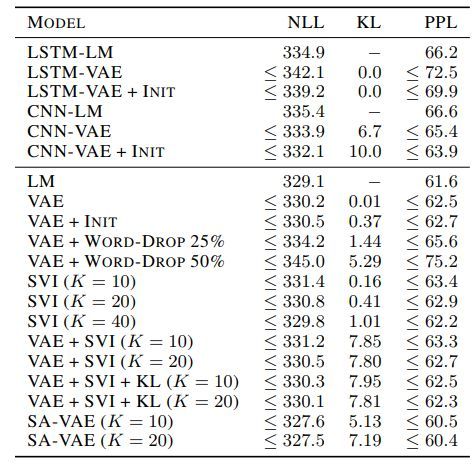
SA-VAE算法伪代码如下
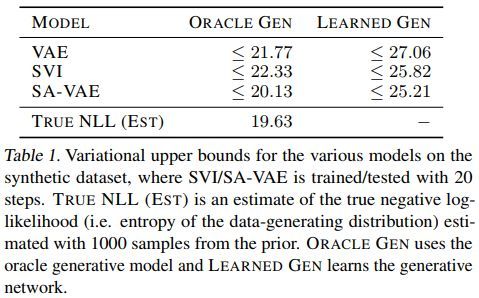
几种方法的效果对比如下
代码地址
https://github.com/harvardnlp/sa-vae
[6] Transformation Autoregressive Networks
Junier B Oliva, Avinava Dubey, Manzil Zaheer, Barnabas P ´ oczos ´,Ruslan Salakhutdinov, Eric P Xing, Jeff Schneider
University of North Carolina, Carnegie Mellon University
http://proceedings.mlr.press/v80/oliva18a/oliva18a.pdf
这篇文章试图对密度估计进行系统整理。现存方法可以分为:自回归模型来估计链式法则的条件因子;基于简单基的变量的非线性变换。基于对这些类别的研究,这篇文章针对每个类提出多种新方法,比如,提出的基于RNN的变换法可以对非马尔科夫连依赖进行建模。通过大量基于真是数据和合成数据的研究,可以对变量和自回归条件模型进行联合变换,进而可以得到明显的效果提升。
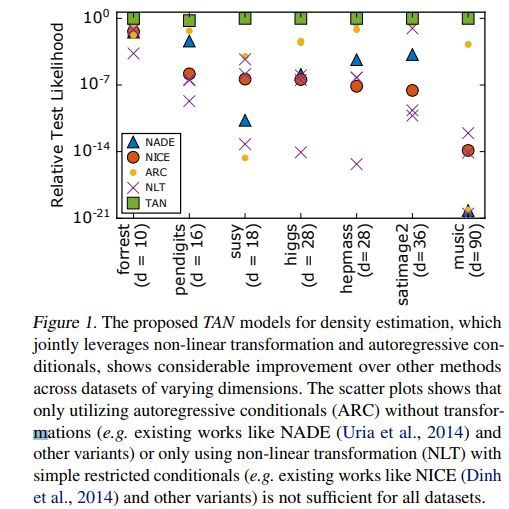
TAN用于密度估计的示例如下
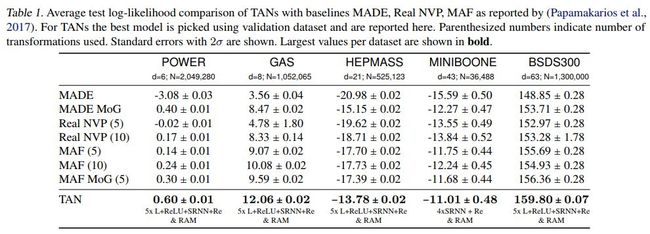
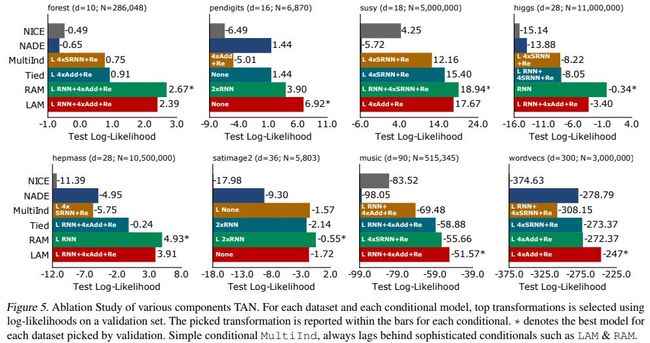
几种方法的效果对比如下
其中made为masked autoencoder for distribution estimation,real nvp 为real-valued non-volume preserving,maf为Masked autoregressive flow for density estimation
代码地址
https://github.com/lupalab/tan
您可能感兴趣