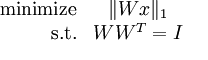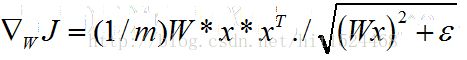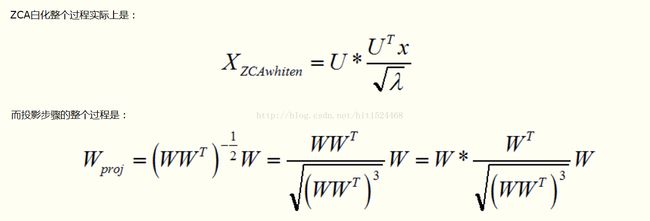独立成分分析及Demo

1. 独立成分分析建模

独立成分分析目标是实现在海量数据中学习完备的单位正交基，所以，所以，可以建立如下的最优化问题：

其中，第一项为稀疏约束，第二项为完备单位正交基约束，熟悉稀疏表示的可能会注意到，为什么上述最优化问题中，没有显式加入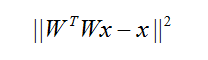约束，因为W为正交矩阵，所以上述误差为0.

2. 独立成分分析最优化问题求解

(1)稀疏约束优化：转化为如下能量泛函的最优化问题

其导数如下：

(2)完备单位正交基约束优化：通过投影实现，投影如下：

 注意，由于我们的完备单位正交基来源于数据，所以，在进行迭代训练前，需要对数据样本进行ZCA White和投影的对比如下：

(3) 优化步骤：

step1: 对训练数据进行中心化、ZCA White处理

step2:根据梯度下降法更新W

step3:对W进行投影

step4:是否满足收敛条件，满足则结束，否则重复step2-3;

(4) 示例代码：

%% CS294A/CS294W Independent Component Analysis (ICA) Exercise

%  Instructions
%  ------------
% 
%  This file contains code that helps you get started on the
%  ICA exercise. In this exercise, you will need to modify
%  orthonormalICACost.m and a small part of this file, ICAExercise.m.

%%======================================================================
%% STEP 0: Initialization
%  Here we initialize some parameters used for the exercise.

numPatches = 20000;
numFeatures = 121;
imageChannels = 3;
patchDim = 8;
visibleSize = patchDim * patchDim * imageChannels;

outputDir = '.';
epsilon = 1e-6; % L1-regularisation epsilon |Wx| ~ sqrt((Wx).^2 + epsilon)

%%======================================================================
%% STEP 1: Sample patches

patches = load('stlSampledPatches.mat');
patches = patches.patches(:, 1:numPatches);
displayColorNetwork(patches(:, 1:100));

%%======================================================================
%% STEP 2: ZCA whiten patches
%  In this step, we ZCA whiten the sampled patches. This is necessary for
%  orthonormal ICA to work.

patches = patches / 255;
meanPatch = mean(patches, 2);
patches = bsxfun(@minus, patches, meanPatch);
% 数据进行ZCA White处理
sigma = patches * patches';
[u, s, v] = svd(sigma);
ZCAWhite = u * diag(1 ./ sqrt(diag(s))) * u';
patches = ZCAWhite * patches;

%%======================================================================
%% STEP 3: ICA cost functions
%  Implement the cost function for orthornomal ICA (you don't have to 
%  enforce the orthonormality constraint in the cost function) 
%  in the function orthonormalICACost in orthonormalICACost.m.
%  Once you have implemented the function, check the gradient.

% Use less features and smaller patches for speed
debug = false; % 置为true时，进行梯度计算验证
if debug
numFeatures = 5;
patches = patches(1:3, 1:5);
visibleSize = 3;
numPatches = 5;

weightMatrix = rand(numFeatures, visibleSize);

[cost, grad] = orthonormalICACost(weightMatrix, visibleSize, numFeatures, patches, epsilon);

numGrad = computeNumericalGradient( @(x) orthonormalICACost(x, visibleSize, numFeatures, patches, epsilon), weightMatrix(:) );
% Uncomment to display the numeric and analytic gradients side-by-side
% disp([numGrad grad]); 
diff = norm(numGrad-grad)/norm(numGrad+grad);
fprintf('Orthonormal ICA difference: %g\n', diff);
assert(diff < 1e-7, 'Difference too large. Check your analytic gradients.');

fprintf('Congratulations! Your gradients seem okay.\n');
end
%%======================================================================
%% STEP 4: Optimization for orthonormal ICA
%  Optimize for the orthonormal ICA objective, enforcing the orthonormality
%  constraint. Code has been provided to do the gradient descent with a
%  backtracking line search using the orthonormalICACost function 
%  (for more information about backtracking line search, you can read the 
%  appendix of the exercise).
%
%  However, you will need to write code to enforce the orthonormality 
%  constraint by projecting weightMatrix back into the space of matrices 
%  satisfying WW^T  = I.
%
%  Once you are done, you can run the code. 10000 iterations of gradient
%  descent will take around 2 hours, and only a few bases will be
%  completely learned within 10000 iterations. This highlights one of the
%  weaknesses of orthonormal ICA - it is difficult to optimize for the
%  objective function while enforcing the orthonormality constraint - 
%  convergence using gradient descent and projection is very slow.

weightMatrix = rand(numFeatures, visibleSize);

[cost, grad] = orthonormalICACost(weightMatrix(:), visibleSize, numFeatures, patches, epsilon);% 计算梯度

fprintf('%11s%16s%10s\n','Iteration','Cost','t');

startTime = tic();

% Initialize some parameters for the backtracking line search
alpha = 0.5;
t = 0.02;
lastCost = 1e40;

% Do 10000 iterations of gradient descent
for iteration = 1:50000
                       
    grad = reshape(grad, size(weightMatrix));
    newCost = Inf;        
    linearDelta = sum(sum(grad .* grad));
    
    % Perform the backtracking line search
    while 1
        considerWeightMatrix = weightMatrix - alpha * grad; %梯度下降法更新W
        % -------------------- YOUR CODE HERE --------------------
        % Instructions:
        %   Write code to project considerWeightMatrix back into the space
        %   of matrices satisfying WW^T = I.
        %   
        %   Once that is done, verify that your projection is correct by 
        %   using the checking code below. After you have verified your
        %   code, comment out the checking code before running the
        %   optimization.
        
%         % Project considerWeightMatrix such that it satisfies WW^T = I
%         error('Fill in the code for the projection here');        
        considerWeightMatrix = (considerWeightMatrix*considerWeightMatrix')^(-0.5)*considerWeightMatrix; % W进行投影
        % Verify that the projection is correct
        temp = considerWeightMatrix * considerWeightMatrix';
        temp = temp - eye(numFeatures);
        assert(sum(temp(:).^2) < 1e-23, 'considerWeightMatrix does not satisfy WW^T = I. Check your projection again');
%         error('Projection seems okay. Comment out verification code before running optimization.');
        
        % -------------------- YOUR CODE HERE --------------------                                        

        [newCost, newGrad] = orthonormalICACost(considerWeightMatrix(:), visibleSize, numFeatures, patches, epsilon);
        if newCost > lastCost - alpha * t * linearDelta
%             fprintf('   %14.6f  %14.6f\n', newCost, lastCost - alpha * t * linearDelta);
            t = 0.9 * t;
        else
            break;
        end
    end
   
    lastCost = newCost;
    weightMatrix = considerWeightMatrix;
    
    fprintf('  %9d  %14.6f  %8.7g\n', iteration, newCost, t);
    
    t = 1.1 * t;
    
    cost = newCost;
    grad = newGrad;
           
    % Visualize the learned bases as we go along    
    if mod(iteration, 1000) == 0
        duration = toc(startTime);
        % Visualize the learned bases over time in different figures so 
        % we can get a feel for the slow rate of convergence
        figure(floor(iteration /  1000));
        displayColorNetwork(weightMatrix'); 
    end
                   
end

% Visualize the learned bases
displayColorNetwork(weightMatrix');

% function [cost, grad] = orthonormalICACost(theta, visibleSize, numFeatures, patches, epsilon)
% %orthonormalICACost - compute the cost and gradients for orthonormal ICA
% %                     (i.e. compute the cost ||Wx||_1 and its gradient)
% 
%     weightMatrix = reshape(theta, numFeatures, visibleSize);
%     
%     cost = 0;
%     grad = zeros(numFeatures, visibleSize);
%     
%     % -------------------- YOUR CODE HERE --------------------
%     % Instructions:
%     %   Write code to compute the cost and gradient with respect to the
%     %   weights given in weightMatrix.     
%     % -------------------- YOUR CODE HERE --------------------     
%     num_samples = size(patches,2); %样本个数
% 
%     aux1 = sqrt(((weightMatrix*patches).^2) + epsilon);
%     cost = sum(aux1(:))/num_samples;
%     grad = ((weightMatrix*patches)./aux1)*patches'./num_samples;
%     grad = grad(:);
% 
% end
% 
function [cost, grad] = orthonormalICACost(theta, visibleSize, numFeatures, patches, epsilon)
%orthonormalICACost - compute the cost and gradients for orthonormal ICA
%                     (i.e. compute the cost ||Wx||_1 and its gradient)

    weightMatrix = reshape(theta, numFeatures, visibleSize);
    
    cost = 0;
    grad = zeros(numFeatures, visibleSize);
    
    % -------------------- YOUR CODE HERE --------------------
    % Instructions:
    %   Write code to compute the cost and gradient with respect to the
    %   weights given in weightMatrix.     
    % -------------------- YOUR CODE HERE --------------------     

%% 方法
      lambda =  8e-6;% 0.5e-4
    num_samples = size(patches,2);
    
    cost_part1 = sum(sum((weightMatrix'*weightMatrix*patches-patches).^2))./num_samples;
    cost_part2 = sum(sum(sqrt((weightMatrix*patches).^2+epsilon)))*lambda;
    cost = cost_part1  +  cost_part2;
    grad = (2*weightMatrix*(weightMatrix'*weightMatrix*patches-patches)*patches'+...
        2*weightMatrix*patches*(weightMatrix'*weightMatrix*patches-patches)')./num_samples+...
        (weightMatrix*patches./sqrt((weightMatrix*patches).^2+epsilon))*patches'*lambda;
    
    grad = grad(:);
    fprintf('%11s%16s\n','cost_part1','cost_part2');
    fprintf('   %14.6f  %14.6f\n', cost_part1, cost_part2);
    
end

注意：计算梯度时，将||w'wx-x||^2的带入求导了！

function numgrad = computeNumericalGradient(J, theta)
% numgrad = computeNumericalGradient(J, theta)
% theta: a vector of parameters
% J: a function that outputs a real-number. Calling y = J(theta) will return the
% function value at theta. 
  
% Initialize numgrad with zeros
numgrad = zeros(size(theta));

%% ---------- YOUR CODE HERE --------------------------------------
% Instructions: 
% Implement numerical gradient checking, and return the result in numgrad.  
% (See Section 2.3 of the lecture notes.)
% You should write code so that numgrad(i) is (the numerical approximation to) the 
% partial derivative of J with respect to the i-th input argument, evaluated at theta.  
% I.e., numgrad(i) should be the (approximately) the partial derivative of J with 
% respect to theta(i).
%                
% Hint: You will probably want to compute the elements of numgrad one at a time. 

epsilon = 1e-8;
n = size(theta,1);
E = eye(n);
for i = 1:n
    delta = E(:,i)*epsilon;
    numgrad(i) = (J(theta+delta)-J(theta-delta))/(epsilon*2.0);
end
%% ---------------------------------------------------------------
end

function displayColorNetwork(A)

% display receptive field(s) or basis vector(s) for image patches
%
% A         the basis, with patches as column vectors

% In case the midpoint is not set at 0, we shift it dynamically
if min(A(:)) >= 0
    A = A - mean(A(:));
end

cols = round(sqrt(size(A, 2)));

channel_size = size(A,1) / 3;
dim = sqrt(channel_size);
dimp = dim+1;
rows = ceil(size(A,2)/cols);
B = A(1:channel_size,:);
C = A(channel_size+1:channel_size*2,:);
D = A(2*channel_size+1:channel_size*3,:);
B=B./(ones(size(B,1),1)*max(abs(B)));
C=C./(ones(size(C,1),1)*max(abs(C)));
D=D./(ones(size(D,1),1)*max(abs(D)));
% Initialization of the image
I = ones(dim*rows+rows-1,dim*cols+cols-1,3);

%Transfer features to this image matrix
for i=0:rows-1
  for j=0:cols-1
      
    if i*cols+j+1 > size(B, 2)
        break
    end
    
    % This sets the patch
    I(i*dimp+1:i*dimp+dim,j*dimp+1:j*dimp+dim,1) = ...
         reshape(B(:,i*cols+j+1),[dim dim]);
    I(i*dimp+1:i*dimp+dim,j*dimp+1:j*dimp+dim,2) = ...
         reshape(C(:,i*cols+j+1),[dim dim]);
    I(i*dimp+1:i*dimp+dim,j*dimp+1:j*dimp+dim,3) = ...
         reshape(D(:,i*cols+j+1),[dim dim]);

  end
end

I = I + 1;
I = I / 2;
imagesc(I); 
axis equal
axis off

end

显示前100个样本如下：

迭代10000次时，训练获得的完备单位正交基

参考：

http://www.cnblogs.com/dmzhuo/p/5009274.html

http://deeplearning.stanford.edu/wiki/index.php/Exercise:Independent_Component_Analysis