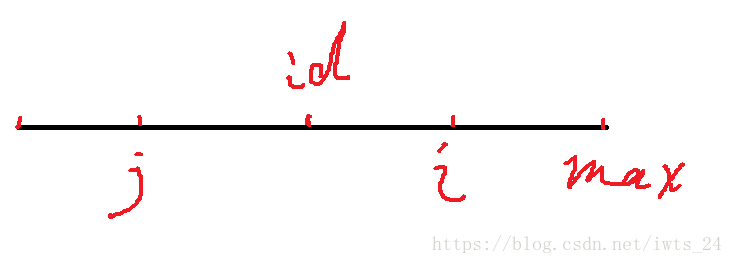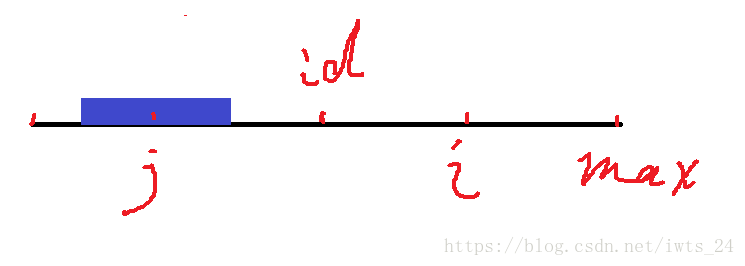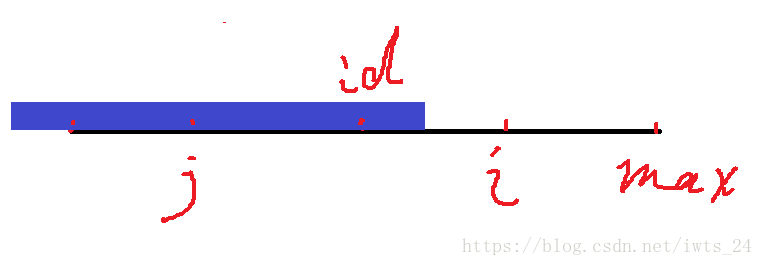Manachar 算法

关于Manachar

        Manachar主要是为了处理回文串问题，回文串的定义不再赘述。一般来讲，判定一个字符串中的子串是否是回文串，常规的方法是遍历字符串的每一个字符，然后向左右扩展，这样可以判定是否是回文串、回文串的长度，以及字符串中最长的回文子串是什么。这样的方法比较暴力，算法复杂度是，实际使用上是比较慢了。1975年，Manachar发明了Manachar算法，能以的算法复杂度来处理这个问题。速度还是比较快的。

比较方便的一个预处理

        貌似很多资料说是Manachar先提出的这个处理方法，不过不仅仅只适用于Manachar，关于字符串，这样的预处理能提供很多新的思路。一般判定回文串要分开判定奇偶，但是如果在字符串中插入从未使用的字符，能够将所有的字符串都按照奇串来考虑，同时不影响是否是回文。例如：

string str = "abababa";
string str_manachar = "*#a#b#a#b#a#b#a#";

这样，所有的串全部转化为奇串，特殊字符随便选择，只要没有在字符串中出现即可。最开始位置的*主要是防止越界，边界处理比较好的也可以不用，#则是穿插在字符中间。这样处理字符串，利用数学公式，会比较方便地更换，代码：

for(int i = len;i >= 0;i--){
    s[i+i+2] = s[i];
    s[i+i+1] = '#';
}

这样反向处理比较节省空间。

P数组的处理

        Manachar的核心在于p数组的创建。p[i]储存了以i位置为中心的字符串的回文长度，简单给出一个表格：

	0	1	2	3	4	5	6	7	8	9
str	*	#	a	#	b	#	a	#	b	#
p		1	2	1	4	1	4	1	2	1

可以看出，p[i]就是包括当前位置在内的回文一侧的长度，回文串包括特殊符号的总长度则是，原串的回文长度则是。所以abba这样的字符串，会变成*#a#b#b#a#，而最中间的#符号对应的值是5，这样就定义了偶回文串的位置与长度。利用p数组，我们就可以找到所有的回文子串，即值>2的就是回文串的中心位置。

        那么Manachar主要就是求p数组了，之前提过p数组的时间复杂度是，换而言之，我们需要在遍历一遍字符串的情况下构造出来p数组。

介绍一下上图，直线代表一个回文串，id是中心轴，i是右边部分的一个点，j是i的一个对称点，max是回文串的边界，也就是最右边的位置。算法主要就从这部分展开，有这样的代码：

if(p[id] + id > i){
    p[i] = p[2*id - i] < p[id]+id-i ? p[2*id - i] : p[id]+id-i;
}else{
    p[i] = 1;
}

前提是在遍历整个数组的情况下，求p[i]的值，p[id]+id就是图中的max的位置，而p[i]就是i，p[2*id - i]就是p[j]。因为我们知道i的位置，j是i关于id位置的对称点，可以这样来计算出j的值。if语句的判定，可以知道此时i是一定在一个回文串中的，那么p[i]就一定是p[j]和[i,max]的最小值。下面分析一下这个结论：

上图是j的回文在id的回文串内的情况，很明显，由于大家都在id的回文串内，一个左一个右，那么i的回文一定跟j一样，而此时p[j] < max-i。而恰好相等也可以适用于这个情况，临界条件没有必要讨论。

上图是j的回文已经超出id的回文串范围的情况，那么实际上说明了id回文串的一侧是回文串，对于i而言，[id,max]范围一定是回文串，而超出的就不一定了，注意这里没有说一定不是，而是不一定，所以p[i]此时至少是max-i，我们之后还需要继续处理。此时p[j]>max-i，而我们选择的是max-i。

        以上两种情况，可以说明上面代码的含义了，那么在i不属于id字符串的情况下，因为没有了j位置的参照，所以最小是1，我们要继续处理，看是否能加长。

        不管怎样，我们对于i位置的初步处理就完成了，现在就考虑是否能使i长度变长，那么我们就利用对称这个性质，使用while循环，看两侧在扩展过程中能有几个字符相同。有代码：

while(s[i - p[i]] == s[i + p[i]]){
    p[i]++;
}

简单的数学计算就直接定位了两侧位置。while循环一直比较就可以了。这里不用考虑越界问题，因为预处理的时候s[0]已经用区别于#的特殊符号覆盖了，所以一定不会越界（到0的时候已经结束循环）。

        还有一点就是id的更换问题，之前是默认id是已知的，实际上id一直在变动。其实这个简单，我们对i的处理是在id回文串的范围内的，也就是[id-p[id],id+p[id]]，那么如果i的回文串已经超出id字符串范围，那么就更新id为i，否则就继续用这个id。这样就能一直遍历i了。manachar核心代码如下：

for(int i = 2;i < 2*len + 1;i++){
    if(p[id] + id > i){
        p[i] = p[2*id - i] < p[id]+id-i ? p[2*id - i] : p[id]+id-i;
    }else{
        p[i] = 1;
    }
    while(s[i - p[i]] == s[i + p[i]]){
        p[i]++;
    }
    if(id + p[id] < i + p[i]){
        id = i;
    }
}

Manachar 算法模板

#include
#include
#include
#define TIME std::ios::sync_with_stdio(false)

// 注意由于要插入'#'，所以没有使用string，而是全局设置了字符串s与p数组
const int MAX=110000+10;  
char s[MAX*2];  
int p[MAX*2]; 

using namespace std;

int manachar(){
	memset(p,0,sizeof(p));
    int len = strlen(s);
    int id = 0;
    int maxlen = 0;
    // 防止偶数串，字符间穿插'#'，但s[0]为'*'
    for(int i = len;i >= 0;i--){
        s[i+i+2] = s[i];
        s[i+i+1] = '#';
    }
    s[0] = '*';
    // manachar核心代码，O(n)复杂度下补充p数组，并求得maxlen
    for(int i = 2;i < 2*len + 1;i++){
        if(p[id] + id > i){
            p[i] = p[2*id - i] < p[id]+id-i ? p[2*id - i] : p[id]+id-i;
        }else{
            p[i] = 1;
        }
        while(s[i - p[i]] == s[i + p[i]]){
            p[i]++;
        }
        if(id + p[id] < i + p[i]){
            id = i;
        }
        if(maxlen < p[i]){
            maxlen = p[i];
        }
    }
    // 得到的maxlen是半径长度，包括了插入的'#'
    return maxlen-1;
}

int main() {
    TIME;
    while (scanf("%s",s) != EOF) {
        int ans = manachar();
        cout << ans << endl;
    }

    system("pause");
    return 0;
}

Manachar 模板的作用与局限

        Manachar算法其实有点类似KMP了，模板其实就有很多种，但是其实都是其核心思想的一个应用。以上面的模板为例，主要是返回最长子回文串的长度。那么我们统计i不为2的数量就可以得到子回文串的总数。Manachar仅仅是处理了字符串，利用p数组完成各种操作，KMP也是处理了字符串，利用next数组完成各种操作（跟前缀有关）。所以Manachar模板实际上还是作用不太大的，主要还是理解吧，如何利用p数组才是核心。