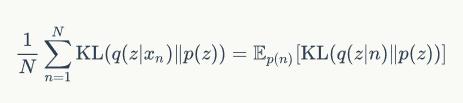VAE系解纠缠：从VAE到βVAE，再到β-TCVAE

   作者：佚   名           

编辑：陈人和           

前  言

“演讲中，Bengio 以去年发布在 arXiv 的研究计划论文「有意识先验」（The consciousness prior）为主旨，重申了他与 Yann Lecun 十年前提出的解纠缠（disentangle）观念：我们应该以「关键要素需要彼此解纠缠」为约束，学习用于描述整个世界的高维表征（unconscious state）、用于推理的低维特征（conscious state），以及从高维到低维的注意力机制——这正是深度学习通往人类水平 AI 的挑战。”Yoshua Bengio首次中国演讲：深度学习通往人类水平AI的挑战。

解纠缠（Disentanglement），也叫做解耦，就是将原始数据空间中纠缠着的数据变化，变换到一个好的表征空间中，在这个空间中，不同要素的变化是可以彼此分离的。比如，人脸数据集经过编码器，在潜变量空间Z中，我们就会获得人脸是否微笑、头发颜色、方位角等信息的分离表示，我们把这些分离表示称为Factors。

解纠缠的方法不仅限于VAE，像传统的机器学习算法PCA也可以理解为一种解纠缠的方法。

章节目录

• VAE

• β-VAE

• β-TCVAE

• 对比结果

01

VAE

Auto-Encoding Variational Bayes：https://arxiv.org/abs/1312.6114

 VAE是将概率图模型的思想和AE（Auto Encoder）的结合体。

看左图的一个概率图模型，假设有一个已知的先验分布P(z)，和能观察到的数据x。我们想要推断后验分布p(z|x),他的计算公式就是下面这个贝叶斯公式。但是当z的维度很高的时候，p(x)的计算是不可行的。这时候我们就设计一个q(z|x)去近似p(z|x)。这个度量就由KL散度给出，通过最小化KL散度，我们就能得到近似的p(z|x)。通过变换，我们就得到下面这个式子,这个式子就等于logp(x)的期望，这个式子也叫做变分下界。最大化这个式子，我们就能近似得到p(x)。 

将这个概率图模型和自编码器结合，我们就得到了右图中的变分自编码器结构。变分自编码器的encoder就可以表示为近似方法q(z|x).

因为VAE的最终目的就是要拟合出x的分布，所以同样的,VAE也要去最大化这个变分下界。写成的loss的形式就是，最小化这个下界。

它包含两个值，一个是对生成的x的期望，一个是拟合的q(z|x)和先验p(z)的KL散度。

这里的q和p分别被phi 和 theta参数化。

VAE的loss:

02

β-VAE

beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework：https://openreview.net/forum?id=Sy2fzU9gl

β-VAE是VAE的变体，增强了VAE模型表示解纠缠的能力。回顾VAE，我们希望最大化生成真实数据的概率值和最小化真实和估计后验分布的KL散度。

相应的拉格朗日函数为：

这样上式的优化问题就可以表示成最大化这个拉格朗日方程，loss函数就可以写成

这里，拉格朗日乘子beta就是一个超参数，当beta为1的时候，它就是标准的VAE。一个较高的beta值，就使得前变量空间z表示信息的丰富度降低，但同时模型的解纠缠能力增加。所以beta可以作为表示能力和解纠缠能力之间的平衡因子。

03

β-TCVAE

Isolating Sources of Disentanglement in VAEs：

https://arxiv.org/abs/1802.04942

接下来就是betatcvae的工作，作者认为虽然βvae很好的提升了vae解纠缠能力，但是并没有解释清楚为什么加重惩罚KL项就可以提升解纠缠能力。

分解ELBO

于是作者对变分下界中的KL散度进行了分解。首先对每个训练样本指定了唯一的索引，并且定义一个在1..N上的均匀的随机变量与训练样本相关联。这个n就代表了索引信息。q(z)就被称为聚合后验，它表示了潜变量的聚合构成。 

经过作者的分解，变分下届中的KL散度就被分解成了三个子KL散度。中间的变换过程就不看了。直接看下这三个子KL散度的含义。

1第一项是索引编码互信息，它与数据变量和潜变量之间的互信息相关。更高的MI表示更好的解纠缠效果。有些研究认为越高的互信息值代表着越好的解纠缠效果，所以可以完全放弃对该项的惩罚。但是有些研究认为对该项惩罚也可以鼓励更好的解纠缠效果。

2第二项是全相关。这是信息论里的概念，它代表着潜变量空间中变量之间的相互依赖程度，是一种冗余度的测量。这里的代表潜变量的第j维。全相关作为惩罚使得模型在分布中去找统计独立性因子，对TC更重的惩罚，代表着后验概率分布中语义的统计独立性更强，加强解纠缠的能力。当都独立时，此项为0，可以理解为最理想的解纠缠效果。

3第三项维度KL散度，代表每个潜变量的维度与先验潜变量的维度不能偏离太大。

通过分解ELBO，作者认为betaVAE成功的原因就在于TC项的作用。它鼓励更低的TC值，同时惩罚了index-code MI，更低的TC是βVAE表现优异的核心所在。 

作者认为在解纠缠的目的中，最重要的就是对TC项进行惩罚，在后续的实验中作者会证实，只惩罚TC项，就可以得到很好的解纠缠效果。

用小批量权重采样来训练

 在作者的分解形式中，存在着q(z)不能直接计算出来的问题，它需要整个训练集，所以作者借鉴了重要性采样的思路，提出了批量权重采样的方法来估计q(z)。 

这里作者采样M个数据，估计方程就可以写成下式： 

其中z(ni)是从条件分布q(z|ni)中的采样。并且这个估计值是有偏的。同时，计算它并不需要额外的超参数。

这样在计算出了分解项之后，就可以对分解后的变分下界分解项进行单独的权重赋值。这就引出了βTCVAE的算法。β-TCVAE的loss如下式: 

作者在实验后证明只调节beta，可以取得最好的结果，证实了TC项是在解纠缠中的重要性。所以作者把α和γ设置成了1，只调节β。

MIG(Mutual Information Gap)

β-TCVAE的文章中提出了一种新的解纠缠的度量方法-MIG互信息间隔，取代了传统的分类度量的方法。潜变量和一个真实因子之间的经验互信息可以用一个联合分布。假设潜变量因子和生成过程已知，互信息就是下面这个式子。其中是潜变量的香农熵。

但是可能会出现一种情况，就是一个factor Vk，可能与多个Zj有很高的互信息，可是我们只希望有一个最大的互信息值，那么就使用下面的公式，每对互信息值减去第二大的互信息值，让其他的Z变小。

这个公式就是最终的度量函数。作者认为他的这种方法的优点就是轴对齐的，就是一个潜变量 之和一个真实的 相关。

04

对比结果

在β-TCVAE中为使用了两个数据集在变分下界和解耦能力上的测验，分别是2d的形状数据集和3D的人脸数据集。这两个数据集的真实因子如图表所示。

从下面的结果图可以看出，当β值升高，互信息的惩罚在βvae中更大，但是他也阻碍了潜变量中更多有用的信息，所以通过互信息度量可以看出β-tcvae有更高的值。这里facflow没有去了解。

然后是隐变量中因子之间分布的相关性和独立性对互信息的影响。作者在两个因子的分布上设置了四种不同的取值，作为模拟的噪声，测试了模型对噪声的鲁棒性，从右箱线图中可以看出β-TCVAE的优越性。

然后是一些定性的比较，从图六中可以看到在3D椅子数据集上，βVAE只可以学到方位角、尺寸等四种属性，而βTCVEA可以多学到椅子材质、椅子腿的旋转的属性。

参考资料

From Autoencoder to Beta-VAE ：

https://lilianweng.github.io/lil-log/2018/08/12/from-autoencoder-to-beta-vae.html

Intuitively Understanding Variational Autoencoders ：

https://towardsdatascience.com/intuitively-understanding-variational-autoencoders-1bfe67eb5daf

Variational autoencoders：

https://www.jeremyjordan.me/variational-autoencoders/

 

END

往期回顾

【1】 

【2】 

【3】 

【4】 

【5】 

机器学习算法工程师

---

                            一个用心的公众号

长按，识别，加关注

进群，学习，得帮助

你的关注，我们的热度，

我们一定给你学习最大的帮助