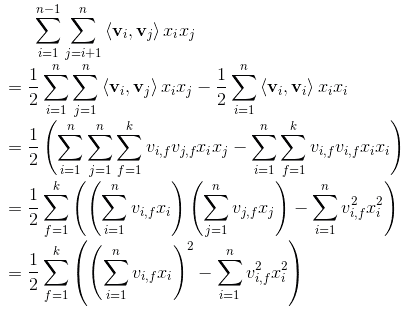【通俗易懂】手把手带你实现DeepFM！

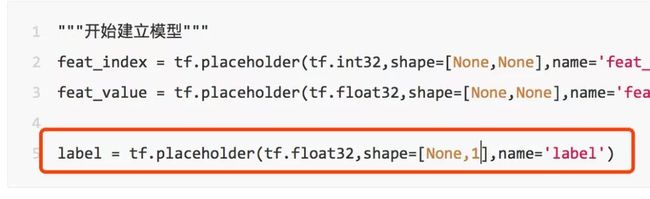
1、模型输入部分，label的shape应该是[None,1]

2、FM一次项的系数应该由feature_bias获得。

可以说，DeepFM是目前最受欢迎的CTR预估模型之一，不仅是在交流群中被大家提及最多的，同时也是在面试中最多被提及的：

1、Deepfm的原理，DeepFM是一个模型还是代表了一类模型，DeepFM对FM做了什么样的改进，FM的公式如何化简并求解梯度（滴滴）

这次咱们一起来回顾一下DeepFM模型，以及手把手来实现一波！

1、DeepFM原理回顾

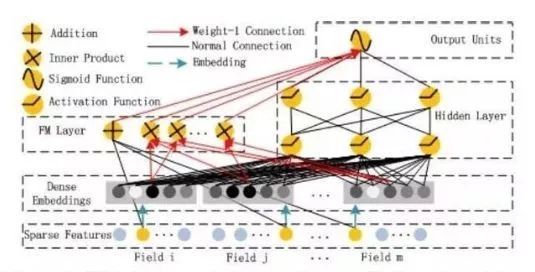
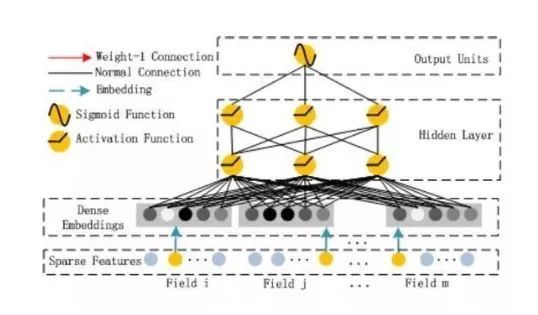
先来回顾一下DeepFM的模型结构：

DeepFM包含两部分：因子分解机部分与神经网络部分，分别负责低阶特征的提取和高阶特征的提取。这两部分共享同样的嵌入层输入。DeepFM的预测结果可以写为：

嵌入层

嵌入层(embedding layer)的结构如上图所示。通过嵌入层，尽管不同field的长度不同（不同离散变量的取值个数可能不同），但是embedding之后向量的长度均为K（我们提前设定好的embedding-size)。通过代码可以发现，在得到embedding之后，我们还将对应的特征值乘到了embedding上，这主要是由于fm部分和dnn部分共享嵌入层作为输入，而fm中的二次项如下：

FM部分

FM部分的详细结构如下：

FM部分是一个因子分解机。关于因子分解机可以参阅文章[Rendle, 2010] Steffen Rendle. Factorization machines. In ICDM, 2010.。因为引入了隐变量的原因，对于几乎不出现或者很少出现的隐变量，FM也可以很好的学习。

FM的输出公式为：

深度部分

深度部分是一个多层前馈神经网络。我们这里不再赘述。

有关模型具体如何操作，我们可以通过代码来进一步加深认识。

2、代码实现

2.1 Embedding介绍

DeepFM中，很重要的一项就是embedding操作，所以我们先来看看什么是embedding，可以简单的理解为，将一个特征转换为一个向量。在推荐系统当中，我们经常会遇到离散变量，如userid、itemid。对于离散变量，我们一般的做法是将其转换为one-hot，但对于itemid这种离散变量，转换成one-hot之后维度非常高，但里面只有一个是1，其余都为0。这种情况下，我们的通常做法就是将其转换为embedding。

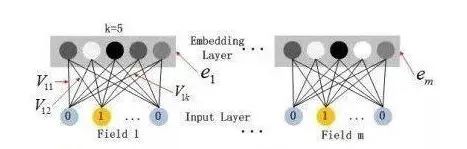
embedding的过程是什么样子的呢？它其实就是一层全连接的神经网络，如下图所示：

假设一个离散变量共有5个取值，也就是说one-hot之后会变成5维，我们想将其转换为embedding表示，其实就是接入了一层全连接神经网络。由于只有一个位置是1，其余位置是0，因此得到的embedding就是与其相连的图中红线上的权重。

2.2 tf.nn.embedding_lookup函数介绍

在tf1.x中，我们使用embedding_lookup函数来实现embedding，代码如下：

# embedding	
embedding = tf.constant(	
        [[0.21,0.41,0.51,0.11]],	
        [0.22,0.42,0.52,0.12],	
        [0.23,0.43,0.53,0.13],	
        [0.24,0.44,0.54,0.14]],dtype=tf.float32)	

	
feature_batch = tf.constant([2,3,1,0])	

	
get_embedding1 = tf.nn.embedding_lookup(embedding,feature_batch)

在embedding_lookup中，第一个参数相当于一个二维的词表，并根据第二个参数中指定的索引，去词表中寻找并返回对应的行。上面的过程为：

注意这里的维度的变化，假设我们的feature_batch 是 1维的tensor，长度为4，而embedding的长度为4，那么得到的结果是 4 * 4 的，同理，假设feature_batch是2 *4的，embedding_lookup后的结果是2 * 4 * 4。每一个索引返回embedding table中的一行，自然维度会+1。

上文说过，embedding层其实是一个全连接神经网络层，那么其过程等价于：

可以得到下面的代码：

embedding = tf.constant(	
    [	
        [0.21,0.41,0.51,0.11],	
        [0.22,0.42,0.52,0.12],	
        [0.23,0.43,0.53,0.13],	
        [0.24,0.44,0.54,0.14]	
    ],dtype=tf.float32)	

	
feature_batch = tf.constant([2,3,1,0])	
feature_batch_one_hot = tf.one_hot(feature_batch,depth=4)	
get_embedding2 = tf.matmul(feature_batch_one_hot,embedding)

二者是否一致呢？我们通过代码来验证一下：

with tf.Session() as sess:	
    sess.run(tf.global_variables_initializer())	
    embedding1,embedding2 = sess.run([get_embedding1,get_embedding2])	
    print(embedding1)	
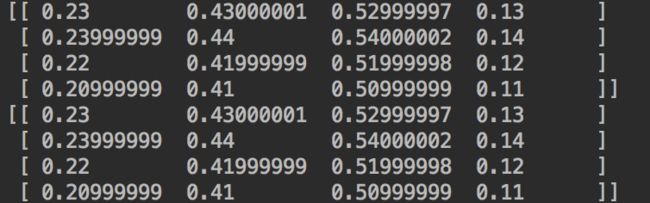
    print(embedding2)

得到的结果为：

二者得到的结果是一致的。

因此，使用embedding_lookup的话，我们不需要将数据转换为one-hot形式，只需要传入对应的feature的index即可。

2.3 数据处理

接下来进入代码实战部分。

首先我们来看看数据处理部分，通过刚才的讲解，想要给每一个特征对应一个k维的embedding，如果我们使用embedding_lookup的话，需要得到连续变量或者离散变量对应的特征索引feature index。听起来好像有点抽象，咱们还是举个简单的例子：

这里有三组特征，或者说3个field的特征，分别是性别、星期几、职业。对应的特征数量分别为2、7、2。我们总的特征数量feature-size为2 + 7 + 2=11。如果转换为one-hot的话，每一个取值都会对应一个特征索引feature-index。

这样，对于一个实例男／二／学生来说，将其转换为对应的特征索引即为0、3、9。在得到特征索引之后，就可以通过embedding_lookup来获取对应特征的embedding。

当然，上面的例子中我们只展示了三个离散变量，对于连续变量，我们也会给它一个对应的特征索引，如：

可以看到，此时共有5个field，一个连续特征就对应一个field。

但是在FM的公式中，不光是embedding的内积，特征取值也同样需要。对于离散变量来说，特征取值就是1，对于连续变量来说，特征取值是其本身，因此，我们想要得到的数据格式如下：

定好了目标之后，咱们就开始实现代码。先看下对应的数据集：

import pandas as pd	

	
TRAIN_FILE = "data/train.csv"	
TEST_FILE = "data/test.csv"	

	
NUMERIC_COLS = [	
    "ps_reg_01", "ps_reg_02", "ps_reg_03",	
    "ps_car_12", "ps_car_13", "ps_car_14", "ps_car_15"	
]	

	
IGNORE_COLS = [	
    "id", "target",	
    "ps_calc_01", "ps_calc_02", "ps_calc_03", "ps_calc_04",	
    "ps_calc_05", "ps_calc_06", "ps_calc_07", "ps_calc_08",	
    "ps_calc_09", "ps_calc_10", "ps_calc_11", "ps_calc_12",	
    "ps_calc_13", "ps_calc_14",	
    "ps_calc_15_bin", "ps_calc_16_bin", "ps_calc_17_bin",	
    "ps_calc_18_bin", "ps_calc_19_bin", "ps_calc_20_bin"	
]	

	
dfTrain = pd.read_csv(TRAIN_FILE)	
dfTest = pd.read_csv(TEST_FILE)	
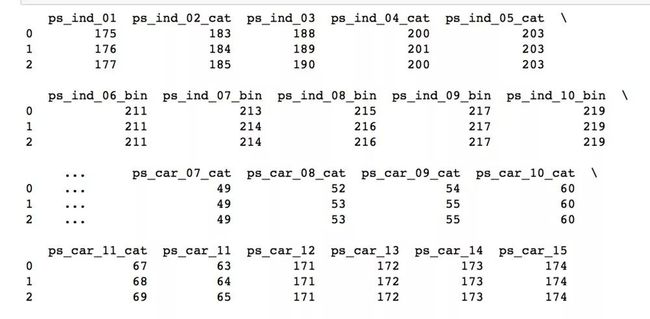
print(dfTrain.head(10))

数据集如下：

我们定义了一些不考虑的变量列、一些连续变量列，剩下的就是离散变量列，接下来，想要得到一个feature-map。这个featrue-map定义了如何将变量的不同取值转换为其对应的特征索引feature-index。

df = pd.concat([dfTrain,dfTest])	

	
feature_dict = {}	
total_feature = 0	
for col in df.columns:	
    if col in IGNORE_COLS:	
continue	
    elif col in NUMERIC_COLS:	
        feature_dict[col] = total_feature	
        total_feature += 1	
    else:	
        unique_val = df[col].unique()	
        feature_dict[col] = dict(zip(unique_val,range(total_feature,len(unique_val) + total_feature)))	
        total_feature += len(unique_val)	
print(total_feature)	
print(feature_dict)

这里，我们定义了total_feature来得到总的特征数量，定义了feature_dict来得到变量取值到特征索引的对应关系，结果如下：

可以看到，对于连续变量，直接是变量名到索引的映射，对于离散变量，内部会嵌套一个二级map，这个二级map定义了该离散变量的不同取值到索引的映射。

下一步，需要将训练集和测试集转换为两个新的数组，分别是feature-index，将每一条数据转换为对应的特征索引，以及feature-value，将每一条数据转换为对应的特征值。

"""	
对训练集进行转化	
"""	
print(dfTrain.columns)	
train_y = dfTrain[['target']].values.tolist()	
dfTrain.drop(['target','id'],axis=1,inplace=True)	
train_feature_index = dfTrain.copy()	
train_feature_value = dfTrain.copy()	

	
for col in train_feature_index.columns:	
    if col in IGNORE_COLS:	
        train_feature_index.drop(col,axis=1,inplace=True)	
        train_feature_value.drop(col,axis=1,inplace=True)	
continue	
    elif col in NUMERIC_COLS:	
        train_feature_index[col] = feature_dict[col]	
    else:	
        train_feature_index[col] = train_feature_index[col].map(feature_dict[col])	
        train_feature_value[col] = 1	

	

	
"""	
对测试集进行转化	
"""	
test_ids = dfTest['id'].values.tolist()	
dfTest.drop(['id'],axis=1,inplace=True)	

	
test_feature_index = dfTest.copy()	
test_feature_value = dfTest.copy()	

	
for col in test_feature_index.columns:	
    if col in IGNORE_COLS:	
        test_feature_index.drop(col,axis=1,inplace=True)	
        test_feature_value.drop(col,axis=1,inplace=True)	
continue	
    elif col in NUMERIC_COLS:	
        test_feature_index[col] = feature_dict[col]	
    else:	
        test_feature_index[col] = test_feature_index[col].map(feature_dict[col])	
        test_feature_value[col] = 1

来看看此时的训练集的特征索引：

对应的特征值：

此时，我们的训练集和测试集就处理完毕了！

2.4 模型参数及输入

接下来定义模型的一些参数，如学习率、embedding的大小、深度网络的参数、激活函数等等，还有两个比较重要的参数，分别是feature的大小和field的大小：

"""模型参数"""	
dfm_params = {	
    "use_fm":True,	
    "use_deep":True,	
    "embedding_size":8,	
    "dropout_fm":[1.0,1.0],	
    "deep_layers":[32,32],	
    "dropout_deep":[0.5,0.5,0.5],	
    "deep_layer_activation":tf.nn.relu,	
    "epoch":30,	
    "batch_size":1024,	
    "learning_rate":0.001,	
    "optimizer":"adam",	
    "batch_norm":1,	
    "batch_norm_decay":0.995,	
    "l2_reg":0.01,	
    "verbose":True,	
    "eval_metric":'gini_norm',	
    "random_seed":3	
}	
dfm_params['feature_size'] = total_feature	
dfm_params['field_size'] = len(train_feature_index.columns)

而训练模型的输入有三个，分别是刚才转换得到的特征索引和特征值，以及label：

"""开始建立模型"""	
feat_index = tf.placeholder(tf.int32,shape=[None,None],name='feat_index')	
feat_value = tf.placeholder(tf.float32,shape=[None,None],name='feat_value')	

	
label = tf.placeholder(tf.float32,shape=[None,1],name='label')

比如刚才的两个数据，对应的输入为：

定义好输入之后，再定义一下模型中所需要的weights：

"""建立weights"""	
weights = dict()	

	
#embeddings	
weights['feature_embeddings'] = tf.Variable(	
    tf.random_normal([dfm_params['feature_size'],dfm_params['embedding_size']],0.0,0.01),	
    name='feature_embeddings')	
weights['feature_bias'] = tf.Variable(tf.random_normal([dfm_params['feature_size'],1],0.0,1.0),name='feature_bias')	

	

	
#deep layers	
num_layer = len(dfm_params['deep_layers'])	
input_size = dfm_params['field_size'] * dfm_params['embedding_size']	
glorot = np.sqrt(2.0/(input_size + dfm_params['deep_layers'][0]))	

	
weights['layer_0'] = tf.Variable(	
    np.random.normal(loc=0,scale=glorot,size=(input_size,dfm_params['deep_layers'][0])),dtype=np.float32	
)	
weights['bias_0'] = tf.Variable(	
    np.random.normal(loc=0,scale=glorot,size=(1,dfm_params['deep_layers'][0])),dtype=np.float32	
)	

	

	
for i in range(1,num_layer):	
    glorot = np.sqrt(2.0 / (dfm_params['deep_layers'][i - 1] + dfm_params['deep_layers'][I]))	
    weights["layer_%d" % i] = tf.Variable(	
        np.random.normal(loc=0, scale=glorot, size=(dfm_params['deep_layers'][i - 1], dfm_params['deep_layers'][i])),	
        dtype=np.float32)  # layers[i-1] * layers[I]	
    weights["bias_%d" % i] = tf.Variable(	
        np.random.normal(loc=0, scale=glorot, size=(1, dfm_params['deep_layers'][i])),	
        dtype=np.float32)  # 1 * layer[I]	

	

	
# final concat projection layer	

	
if dfm_params['use_fm'] and dfm_params['use_deep']:	
    input_size = dfm_params['field_size'] + dfm_params['embedding_size'] + dfm_params['deep_layers'][-1]	
elif dfm_params['use_fm']:	
    input_size = dfm_params['field_size'] + dfm_params['embedding_size']	
elif dfm_params['use_deep']:	
    input_size = dfm_params['deep_layers'][-1]	

	
glorot = np.sqrt(2.0/(input_size + 1))	
weights['concat_projection'] = tf.Variable(np.random.normal(loc=0,scale=glorot,size=(input_size,1)),dtype=np.float32)	
weights['concat_bias'] = tf.Variable(tf.constant(0.01),dtype=np.float32)

介绍两个比较重要的参数，weights['feature_embeddings']是每个特征所对应的embedding，它的大小为feature-size * embedding-size，另一个参数是weights['feature_bias'] ，这个是FM部分计算时所用到的一次项的权重参数，可以理解为embedding-size为1的embedding table，它的大小为feature-size * 1。

假设weights['feature_embeddings']如下：

2.5 嵌入层

嵌入层，主要根据特征索引得到对应特征的embedding：

"""embedding"""	
embeddings = tf.nn.embedding_lookup(weights['feature_embeddings'],feat_index)	

	
reshaped_feat_value = tf.reshape(feat_value,shape=[-1,dfm_params['field_size'],1])	

	
embeddings = tf.multiply(embeddings,reshaped_feat_value)

这里注意的是，在得到对应的embedding之后，还乘上了对应的特征值，这个主要是根据FM的公式得到的。过程表示如下：

2.6 FM部分

我们先来回顾一下FM的公式，以及二次项的化简过程：

上面的式子中有部分同学曾经问我第一步是怎么推导的，其实也不难，看下面的手写过程(大伙可不要嫌弃字丑哟)

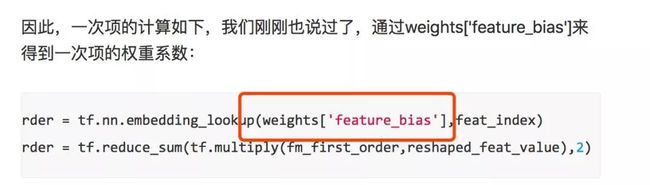
因此，一次项的计算如下，我们刚刚也说过了，通过weights['feature_bias']来得到一次项的权重系数：

fm_first_order = tf.nn.embedding_lookup(weights['feature_bias'],feat_index)	
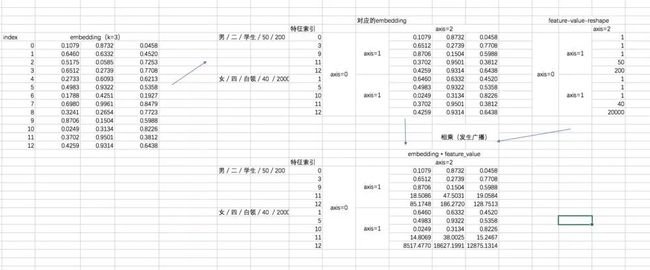
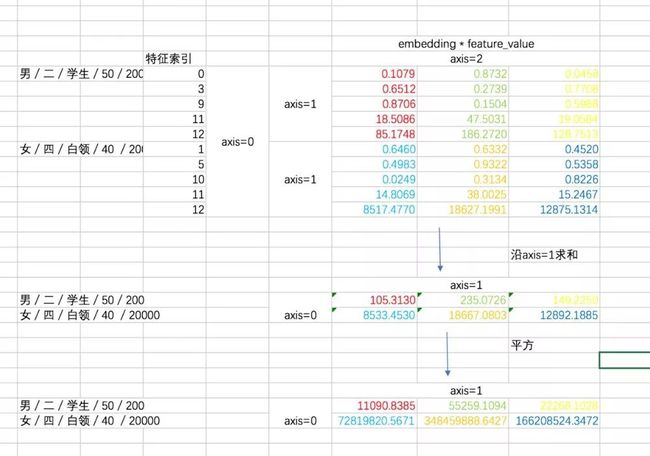
fm_first_order = tf.reduce_sum(tf.multiply(fm_first_order,reshaped_feat_value),2)

对于二次项，经过化简之后有两部分（暂不考虑最外层的求和），我们先用excel来形象展示一下两部分，这有助于你对下面代码的理解。

第一部分过程如下：

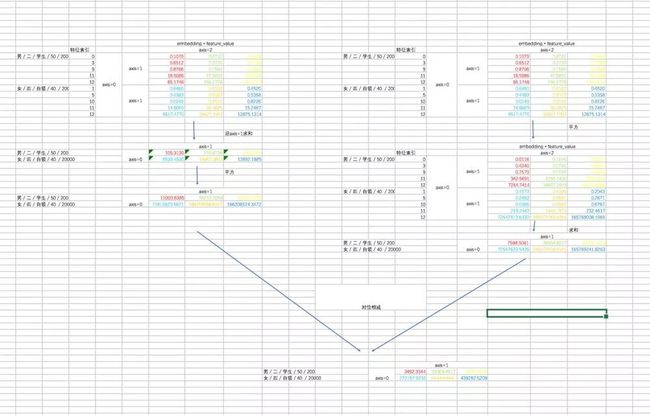
第二部分的过程如下：

最后两部分相减：

二次项部分的代码如下：

summed_features_emb = tf.reduce_sum(embeddings,1)	
summed_features_emb_square = tf.square(summed_features_emb)	

	
squared_features_emb = tf.square(embeddings)	
squared_sum_features_emb = tf.reduce_sum(squared_features_emb,1)	

	
fm_second_order = 0.5 * tf.subtract(summed_features_emb_square,squared_sum_features_emb)	

要注意这里的fm_second_order是二维的tensor，大小为batch-size * embedding-size，也就是公式中最外层的一个求和还没有进行，这也是代码中与FM公式有所出入的地方。我们后面再讲。

2.7 Deep部分

Deep部分很简单了，就是几层全连接的神经网络：

"""deep part"""	
y_deep = tf.reshape(embeddings,shape=[-1,dfm_params['field_size'] * dfm_params['embedding_size']])	

	
for i in range(0,len(dfm_params['deep_layers'])):	
    y_deep = tf.add(tf.matmul(y_deep,weights["layer_%d" %i]), weights["bias_%d"%I])	
    y_deep = tf.nn.relu(y_deep)

2.8 输出部分

最后的输出部分，论文中的公式如下：

在我们的代码中如下：

"""final layer"""	
if dfm_params['use_fm'] and dfm_params['use_deep']:	
    concat_input = tf.concat([fm_first_order,fm_second_order,y_deep],axis=1)	
elif dfm_params['use_fm']:	
    concat_input = tf.concat([fm_first_order,fm_second_order],axis=1)	
elif dfm_params['use_deep']:	
    concat_input = y_deep	
 	
out = tf.nn.sigmoid(tf.add(tf.matmul(concat_input,weights['concat_projection']),weights['concat_bias']))

看似有点出入，其实真的有点出入，不过无碍，咱们做两点说明：

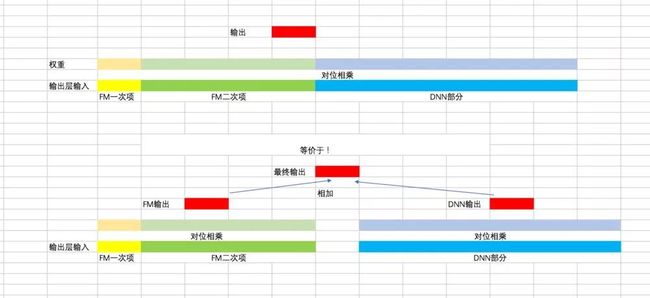
1）首先，这里整体上和最终的公式是相似的，看下面的excel（由于最后一层只有一个神经元，矩阵相乘可以用对位相乘再求和代替）：

2）这里不同的地方就是，FM二次项化简之后最外层不再是简单的相加了，而是变成了加权求和（有点类似attention的意思），如果FM二次项部分对应的权重都是1，就是标准的FM了。

2.9 Loss and Optimizer

这一块也不再多讲，我们使用logloss来指导模型的训练：

"""loss and optimizer"""	
loss = tf.losses.log_loss(tf.reshape(label,(-1,1)), out)	
optimizer = tf.train.AdamOptimizer(learning_rate=dfm_params['learning_rate'], beta1=0.9, beta2=0.999,	
                                                        epsilon=1e-8).minimize(loss)

至此，我们整个DeepFM模型的架构就搭起来了，接下来，我们简单测试一下代码：

"""train"""	
with tf.Session() as sess:	
    sess.run(tf.global_variables_initializer())	
    for i in range(100):	
        epoch_loss,_ = sess.run([loss,optimizer],feed_dict={feat_index:train_feature_index,	
                             feat_value:train_feature_value,	
                             label:train_y})	
        print("epoch %s,loss is %s" % (str(i),str(epoch_loss)))

调试成功：

好了，本次的手把手实现DeepFM教学就到这里了，这个模型大家一定要掌握啊，推荐系统岗位校招必考！

代码链接：https://github.com/princewen/tensorflow_practice/blob/master/recommendation/Basic-DeepFM-model/DeepFM-StepByStep.ipynb

数据在git最外层的readme中。