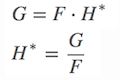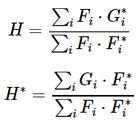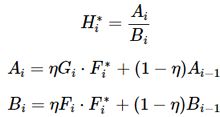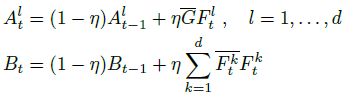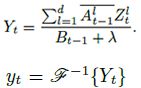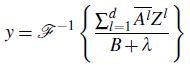目标跟踪之相关滤波:CF及后续改进篇
一. 何为相关滤波?
Correlation Filter 最早应用于信号处理,用来描述两个信号之间的相关性,或者说相似性(有点像早期的概率密度),先来看定义:
对于两个数据 f 和 g,则两个信号的相关性(correlation)为:
其中 f∗ 表示 f 的 复共轭,这是和卷积的区别(相关性 与 卷积 类似,区别就在于里面的共轭)。
PS:复共轭是指 实部不变,虚部取反 (a + b i)* = a - b i; 共轭矩阵是指 矩阵转置后再对每个元素求共轭,不理解的童鞋请查阅百科。
二. CF 在图像的引入 - MOSSE
可以参考经典论文 MOSSE (Minimum Output Sum of Squared Error filter)
论文下载:visual object tracking using adaptive correlation filters
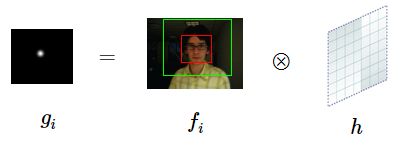
对于图像来讲,问题描述为要找到一个 滤波模版 h,与输入图像 f 求相关性,得到相关图 g。
![]()
为了方便理解,用一幅图来进行说明(相关图 g 描述目标响应,越接近时值越大):
为了加快计算速度,这里引入了傅里叶变换,根据卷积定理(correlation版本)可知,函数互相关的傅里叶变换等于函数傅里叶变换的乘积:
通过上面的公式,将复杂的互相关计算转换成 点乘。注意后面的 F(h) 是共轭,与卷积不同,公式可以简化描述为:
H* 就是我们要求的滤波器,MOSSE 提出的方法就是 最小化平方和误差,也就是针对m个样本 求最小二乘,描述为:
上面公式是将图像展开到像素,每个像素是独立计算的,最小化上面的公式很简单,就是求偏导=0,具体求解过程不再展开,得到最终的求解公式为:
作者提出了一个更新算法,根据当前帧不断进行调整,即在线更新策略,调整策略如下:
其中 η 为学习率,一般设置为 0.1,通过分子分母分别更新。
三. 有一种速度叫 KCF
KCF是一个非常经典的算法(kernelized correlation filters),速度极快,正常可以达到 100+ FPS。
论文下载:High-speed tracking with kernelized correlation filters(ECCV 2012, TPAMI 2015)
Paper及源码下载参考作者主页:http://www.robots.ox.ac.uk/~joao/#
关于 KCF 的介绍可以参考之前的博文:【 机器学习实践系列之5 - 目标跟踪 】
四. 品味经典之 DSST
DSST(Discriminative Scale Space Tracker)是在 MOSSE 基础上的改进,主要在应对尺度变化上(增加了一个 尺度 Correlation Filter),通过两个 Filter 分别跟踪 位置变化(translation)和尺度变化(scale estimation),Translation Filter 专门用于确定新的目标位置,Scale Filter 用来进行尺度估计。
另外 DSST 将原来的灰度特征替换为 HOG 特征,能够对目标特征更好的描述。
论文下载:Accurate Scale Estimation for Robust Visual Tracking
Discriminative Scale Space Tracking
工程及 Matlab 代码可以参考【作者主页】 CPP代码参考(window c++11)【Github】
> 4.1 Filter 合并
DSST 组合成了一个三维的空间滤波器(M*N*S),其中 M*N对应输入Sample宽高(Trans),S对应尺度(Scale)。当然说是组合,实际上是分开独立计算的,先来看一幅图:
1)Translation Filter
对应上图(a),对于当前Sample框(2倍目标大小),对每个像素 提取 d维特征(d-1维的 hog特征 + 1维的灰度特征-最下patch),得到d个 Patch, 在不同特征维度l=[0,d) 上做基于最小二乘的目标函数:
公式中 λ 为正则项,降低 低权重系数的影响,滤波器 通过求偏导得到(公式推导可以看 Paper 的 Appendix):
● 模型训练过程:
为了简化计算,作者采用了 Single Training Sample的方法,只训练当前帧的输入,通过和之前帧的加权平均学习到前面的数据(借鉴了 MOSSE 的参数更新策略):
其中 A、B 分别对应分子、分母,通过上面的公式迭代求解,η 表示应学习率。
● 求解计算过程:
对于 输入样本 Z,根据 响应函数 Y=H* Z,并求 逆向 FFT 得到最大相关滤波响应值 y:
2)Scale Filter
对应上图(b),按照目标位置 {w,h} 进行尺度缩放采样,缩放尺度为 a^n,a=1.02,n=[-16,16],对应采样为 33级别(=S),构成了一个层数为S的金字塔。
对应在每层金字塔上,将 Patch 图像缩放成统一尺寸,提取d维Hog特征,以该特征作为训练样本,得到相关滤波器 H,用来预测输出尺度。
模型更新过程、滤波响应求解过程 与 Translation Filter 一致。
> 4.2 算法描述
输入(input):
a)t 时刻的图像 I(t)
b)上一帧 目标位置 P(t-1) 和尺度 S(t-1)
c)上一帧的位置模型 A_trans(t-1), B_trans(t-1) 和 尺度模型 A_scale(t-1), B_scale(t-1)
输出(output):
a)当前帧的 估计位置 P(t) 和估计尺度 S(t)
b)更新后的位置模型 A_trans(t), B_trans(t) 和 尺度模型 A_scale(t), B_scale(t)
位置估计过程:
1)根据上一帧目标位置 P(t-1) 和尺度 S(t-1),在当前帧图像 I 上,按照2倍目标大小采样,得到 Search 样本 Ztrans;
2)根据上一帧位置模型 A_trans(t-1), B_trans(t-1) ,计算位置响应,公式为:
3)得到目标位置 P(t) = max(y_trans);
位置估计过程:
4)提取不同尺度样本 Ztrans(文中对应33个);
5)与上面同样的方式计算出 y_scale,得到目标尺度 S(t) = max(y_scale);
模型更新过程:
6)从当前帧图像 I(t) 提取 训练样本 f_trans 和 f_scale;
提取对应Hog特征、灰度特征,构造对应尺度的高斯响应函数。
7)更新模型 位置模型 和 尺度模型;
参照上面的模型训练过程。
作者后续在 DSST基础上进行改进,提出了 fDSST,旨在优化算法效率,转发表在 PAMI上,帧率有了 成倍的提升。主要改进思路有两点:一是 相关性插值(sub-grid interpolation of correlation scores),即通过 Coarse Grid 计算 Score,通过插值得到 全分辨率的 Score;二是 通过PCA降维来减少特征维度。都是比较简单的Trick,本文不再展开(Paper 可以参考上面的链接)。
五. VOT2016 排名第一的 C-COT
比赛说明实力,这篇文章来自于 2016年的ECCV,MD大神注定要在 CF 上死磕。
论文下载:Beyond Correlation Filters: Learning Continuous Convolution Operators for Visual Tracking
代码下载:【Github】
传统的相关滤波方法只是用 灰度、Hog 做 Single Sample的特征提取和滤波训练,也许很多人都能想到 要用金字塔,要结合CNN多尺度的卷积特征,思路没错,只是 MD 比你下手快而已。
算法核心思想是:
1)对于Search Region,提取不同分辨率的特征(RGB+Conv特征),对应 第一列;
2)通过针对不同层训练的相关滤波器 进行计算,对应 第二列;
3)得到响应图(Confidence Scores),对应第三列;
4)将响应图 进行累加,得到多个分辨率置信度之和,即为最终的置信图,对应最大值为目标位置;
这篇文章算是过渡阶段的产品,除了引入深度学习的元素之外,其实没有太多的创新点,对于时间充裕的童鞋可以详细看看,否则的话建议忽略。
六. 沿着这条路继续……
相关滤波 带给我们的不只是这些,Visual Tracking 在这条道路上可以走的更远,我们看到了 ECO,还有更远处~你的Paper!
下一篇会针对 ECO 进行专门剖析,希望能和大家多多交流!